Определения и свойства всех рассмотренных в курсе планиметрии операций над векторами (сложение, вычитание, умножение на число, скалярное умножение) не претерпевают никаких изменений:
 Сложение двух векторов по-прежнему выполняется по правилу треугольника или параллелограмма, а сложение нескольких векторов – по правилу многоугольника (с той лишь разницей, что при откладывании следующего вектора-слагаемого от конца предыдущего все векторы «выстраиваются» не в плоскую ломаную линию).
Сложение двух векторов по-прежнему выполняется по правилу треугольника или параллелограмма, а сложение нескольких векторов – по правилу многоугольника (с той лишь разницей, что при откладывании следующего вектора-слагаемого от конца предыдущего все векторы «выстраиваются» не в плоскую ломаную линию).
При сложении трех векторов, отложенных от одной точки, удобно пользоваться так называемым правилом параллелепипеда – аналогом правила параллелограмма: к примеру, на рисунке 51 от точки A отложены векторы 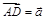 ,
, 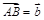 и
и  . В соответствии с правилом параллелограмма,
. В соответствии с правилом параллелограмма,  ; а т.к. ACC 1 A 1 – тоже параллелограмм, то
; а т.к. ACC 1 A 1 – тоже параллелограмм, то  . Таким образом, для сложения трех векторов можно отложить их от одной точки A и построить на них, как на ребрах, параллелепипед. Тогда вектор, построенный на диагонали параллелепипеда, исходящей из точки A, представляет собою сумму трех векторов.
. Таким образом, для сложения трех векторов можно отложить их от одной точки A и построить на них, как на ребрах, параллелепипед. Тогда вектор, построенный на диагонали параллелепипеда, исходящей из точки A, представляет собою сумму трех векторов.
Выполняются следующие очевидные законы сложения векторов:
1.  ;
;
2.  .
.
Также для произвольного числа векторов выполняется неравенство треугольника в векторной форме:
 .
.
Вычитание векторов  и
и  проще всего выполнять путем сложения векторов
проще всего выполнять путем сложения векторов  и
и  :
:  .
.
Произведением вектора  на число k называется вектор
на число k называется вектор  , длина которого равна
, длина которого равна  , а направление совпадает с направлением вектора
, а направление совпадает с направлением вектора  , если k ³ 0, и противоположно направлению вектора
, если k ³ 0, и противоположно направлению вектора  , если k < 0
, если k < 0
Выполняются следующие законы умножения вектора на число:
1.  ;
;
2.  ;
;
3. 
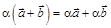 .
.
Операции сложения векторов и умножения вектора на число позволяют решить следующую ключевую задачу (рисунок 52): Если точка K делит отрезок AB в отношении AK: KB = k, а O – произвольная точка пространства, то 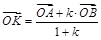 .
.
Из этой задачи вытекает очень полезное следствие: Если M – середина отрезка AB, то для произвольной точки O выполняется равенство:  .
.
Напомним, что коллинеарными называются векторы, лежащие на одной или параллельных прямых. Определение коллинеарных векторов можно сформулировать следующим образом: векторы называются коллинеарными, если при откладывании от одной точки они оказываются лежащими на одной прямой.
В пространстве аналогичным образом вводится понятие компланарных векторов: векторы называются компланарными, если они лежат в одной или параллельных плоскостях. Это определение эквивалентно следующему: векторы в пространстве называются компланарными, если при откладывании от одной точки они оказываются лежащими в одной плоскости. Рассмотрим подробнее вопрос о компланарности двух и трех векторов:
1. Очевидно, что два вектора всегда являются компланарными: при откладывании двух векторов от одной точки они всегда оказываются лежащими в одной плоскости.
2. Три вектора, среди которых есть два коллинеарных, компланарны, поскольку при откладывании их от одной точки коллинеарные векторы оказываются лежащими на одной прямой, а все три вектора – в одной плоскости.
3. Если один из трех векторов  ,
,  и
и  раскладывается по двум другим (к примеру,
раскладывается по двум другим (к примеру,  ), то все три вектора являются компланарными: при откладывании от одной точки векторов
), то все три вектора являются компланарными: при откладывании от одной точки векторов  и
и  они оказываются лежащими в одной плоскости, Þ согласно определению произведения вектора на число, векторы
они оказываются лежащими в одной плоскости, Þ согласно определению произведения вектора на число, векторы  и
и  лежат в этой же плоскости; а по определению суммы двух векторов, вектор
лежат в этой же плоскости; а по определению суммы двух векторов, вектор  также лежит в этой плоскости. Обратно, если вектор
также лежит в этой плоскости. Обратно, если вектор  компланарен паре неколлинеарных векторов
компланарен паре неколлинеарных векторов  и
и  , то при откладывании этих трех векторов от одной точки они оказываются лежащими в одной плоскости, а значит, по теореме о разложении вектора по базису на плоскости,
, то при откладывании этих трех векторов от одной точки они оказываются лежащими в одной плоскости, а значит, по теореме о разложении вектора по базису на плоскости,  . Таким образом, можно сформулировать следующий критерий компланарности трех векторов: Вектор
. Таким образом, можно сформулировать следующий критерий компланарности трех векторов: Вектор  компланарен паре неколлинеарных векторов
компланарен паре неколлинеарных векторов  и
и  тогда и только тогда, когда он раскладывается по векторам
тогда и только тогда, когда он раскладывается по векторам  и
и  .
.
Критерий компланарности трех векторов часто формулируют следующим образом: Три вектора  ,
,  и
и  компланарны тогда и только тогда, когда выполняется равенство
компланарны тогда и только тогда, когда выполняется равенство  , в котором хотя бы одно из чисел a, b или g не равно нулю.
, в котором хотя бы одно из чисел a, b или g не равно нулю.
Покажем, что вторая формулировка критерия компланарности трех векторов эквивалентна первой:
Þ Пусть векторы  ,
,  и
и  компланарны. Если среди них нет коллинеарных, то, согласно первой формулировке критерия компланарности трех векторов, один из них можно разложить по двум другим. Пусть, к примеру,
компланарны. Если среди них нет коллинеарных, то, согласно первой формулировке критерия компланарности трех векторов, один из них можно разложить по двум другим. Пусть, к примеру,  . Прибавив вектор
. Прибавив вектор  к обеим частям этого векторного равенства, получим:
к обеим частям этого векторного равенства, получим: 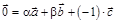 . Таким образом, равенство
. Таким образом, равенство  верно, причем как минимум один из коэффициентов в нем ненулевой: g = –1.
верно, причем как минимум один из коэффициентов в нем ненулевой: g = –1.
В случае, когда среди векторов  ,
,  и
и  есть пара коллинеарных (к примеру,
есть пара коллинеарных (к примеру,  ÷ç
÷ç  ), один из них может оказаться нулевым (например,
), один из них может оказаться нулевым (например, 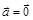 ). В этом случае при любом ненулевом a и нулевых b и g равенство
). В этом случае при любом ненулевом a и нулевых b и g равенство  верно. Если же векторы
верно. Если же векторы  и
и  коллинеарны, и при этом ни один из них не является нулевым, то по лемме о коллинеарных векторах,
коллинеарны, и при этом ни один из них не является нулевым, то по лемме о коллинеарных векторах,  . Прибавив к обеим частям этого равенства вектор
. Прибавив к обеим частям этого равенства вектор 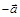 , получим:
, получим:  , т.е. равенство
, т.е. равенство  снова оказывается верным при
снова оказывается верным при  .
.
Ü Пусть теперь выполняется равенство  , в котором хотя бы один из коэффициентов a, b или g ненулевой (для определенности будем считать, что g ¹ 0). Прибавим к обеим частям этого равенства вектор
, в котором хотя бы один из коэффициентов a, b или g ненулевой (для определенности будем считать, что g ¹ 0). Прибавим к обеим частям этого равенства вектор  и поделим обе части полученного равенства на –g:
и поделим обе части полученного равенства на –g: 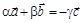 Û
Û 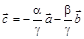 . Таким образом, вектор
. Таким образом, вектор  раскладывается по векторам
раскладывается по векторам  и
и  , а значит, в соответствии с первой формулировкой критерия компланарности трех векторов, векторы
, а значит, в соответствии с первой формулировкой критерия компланарности трех векторов, векторы  ,
,  и
и  компланарны. #
компланарны. #
Аналогично тому, как на плоскости всякий вектор можно разложить по базису из двух неколлинеарных векторов, в пространстве базисом является тройка некомпланарных векторов. Это утверждает теорема о разложении вектора по базису в пространстве: Если векторы  ,
,  и
и  некомпланарны, то всякий вектор
некомпланарны, то всякий вектор  можно разложить по векторам
можно разложить по векторам  ,
,  и
и  единственным образом.
единственным образом.
Дано:
 , ,  , ,  некомпланарны; некомпланарны;
 . .
 Доказать:$! a,! b,! g: Доказать:$! a,! b,! g:
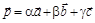 . .
| 
| Доказательство:
$: 1. Прежде всего отметим, что среди векторов  , ,  и и  нет коллинеарных (если среди трех векторов есть пара коллинеарных, то эти векторы компланарны, что противоречит условию). Кроме того, ни один из этих трех векторов не может быть нулевым. нет коллинеарных (если среди трех векторов есть пара коллинеарных, то эти векторы компланарны, что противоречит условию). Кроме того, ни один из этих трех векторов не может быть нулевым.
|
2. Рассмотрим случай, когда вектор  коллинеарен хотя бы одному из векторов коллинеарен хотя бы одному из векторов  , ,  или или  (пусть, к примеру, (пусть, к примеру,  ÷ç ÷ç  ). Тогда по лемме о коллинеарных векторах, ). Тогда по лемме о коллинеарных векторах,  , т.е. вектор , т.е. вектор  раскладывается по векторам раскладывается по векторам  , ,  и и  .
3. Теперь рассмотрим случай, когда среди векторов .
3. Теперь рассмотрим случай, когда среди векторов  , ,  , ,  и и  нет коллинеарных. Выберем в пространстве произвольную точку O и отложим от нее векторы нет коллинеарных. Выберем в пространстве произвольную точку O и отложим от нее векторы 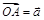 , ,  , ,  и и 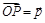 (рисунок 53). По определению некомпланарных векторов, вектор (рисунок 53). По определению некомпланарных векторов, вектор  окажется лежащим вне плоскости p = (AOB).
4. Через точку P проведем прямую PD ÷ç OC: D Î p. Тогда окажется лежащим вне плоскости p = (AOB).
4. Через точку P проведем прямую PD ÷ç OC: D Î p. Тогда  ÷ç ÷ç  , Þ по лемме о коллинеарных векторах, , Þ по лемме о коллинеарных векторах,  .
5. По построению вектор .
5. По построению вектор  лежит в плоскости p, Þ лежит в плоскости p, Þ  .
6. По правилу треугольника, .
6. По правилу треугольника, 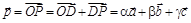 .
!: 7. Допустим, что существуют числа a¢, b¢, g¢: .
!: 7. Допустим, что существуют числа a¢, b¢, g¢:  . Преобразуем векторное равенство: . Преобразуем векторное равенство:  Û Û  . Тогда по критерию компланарности трех векторов либо векторы . Тогда по критерию компланарности трех векторов либо векторы  , ,  и и  компланарны, что противоречит условию, либо компланарны, что противоречит условию, либо 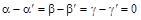 Û a = a¢, b = b¢, g = g¢, т.е. тройка чисел a, b и g единственна. # Û a = a¢, b = b¢, g = g¢, т.е. тройка чисел a, b и g единственна. #
|
Замечание: Тройка некомпланарных векторов  ,
,  и
и  в пространстве называется базисом, а коэффициенты разложения вектора
в пространстве называется базисом, а коэффициенты разложения вектора  по базису – его координатами в этом базисе (если
по базису – его координатами в этом базисе (если 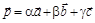 , то {a; b; g} – координаты вектора
, то {a; b; g} – координаты вектора  в базисе {
в базисе {  ;
;  ;
;  }).
}).
Напомним, что скалярным произведением векторов  и
и 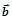 называется число, равное произведению длин векторов
называется число, равное произведению длин векторов  и
и  на косинус угла между ними:
на косинус угла между ними:  . При этом определение угла между векторами не претерпевает никаких изменений: чтобы найти угол между векторами
. При этом определение угла между векторами не претерпевает никаких изменений: чтобы найти угол между векторами  и
и  , необходимо от произвольной точки O пространства отложить векторы
, необходимо от произвольной точки O пространства отложить векторы 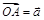 и
и  и найти
и найти  .
.
Из определения скалярного произведения векторов вытекает исключительно полезный критерий ортогональности двух векторов: 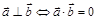 . Кроме того,
. Кроме того,  ;
;  .
.
В курсе планиметрии были доказаны следующие свойства скалярного произведения векторов:
1.  , причем
, причем  Û
Û 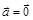 ;
;
2.  (переместительный закон);
(переместительный закон);
3.  (распределительный закон);
(распределительный закон);
4.  (сочетательный закон).
(сочетательный закон).
Все свойства скалярного произведения векторов сохраняют свою силу ив пространстве.
Замечание 1: Для нахождения длины отрезка векторным способом используется тот очевидный факт, что скалярный квадрат вектора равен квадрату его длины:  .
.
Замечание 2: Скалярное произведение векторов активно используется для нахождения угла между прямыми.