Задание 2
| Определение | Квадратной матрице   -го порядка ставиться в соответствие число -го порядка ставиться в соответствие число  , называемое определителем матрицы или детерминантом. , называемое определителем матрицы или детерминантом.
|
· ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ ВТОРОГО ПОРЯДКА
Чтобы вычислить определитель матрицы  второго порядка, надо от произведения элементов главной диагонали отнять произведение элементов побочной диагонали:
второго порядка, надо от произведения элементов главной диагонали отнять произведение элементов побочной диагонали:

| Пример | Задание. Вычислить определитель второго порядка  Решение.
Решение.  Ответ.
Ответ. 
|
· МЕТОДЫВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ ТРЕТЬЕГО ПОРЯДКА
· Правило треугольника
Схематически это правило можно изобразить следующим образом:
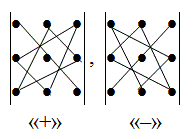
Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком "плюс"; аналогично, для второго определителя - соответствующие произведения берутся со знаком "минус", т.е.
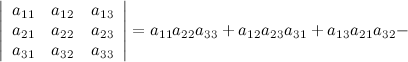

| Пример | Задание. Вычислить определитель  методом треугольников.
Решение. методом треугольников.
Решение. 
 Ответ.
Ответ. 
|
· Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком "плюс"; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком "минус":


| Пример | Задание. Вычислить определитель  с помощью правила Саррюса.
Решение. с помощью правила Саррюса.
Решение. 
 Ответ.
Ответ. 
|
· Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
| Пример | Задание. Разложив по первой строке, вычислить определитель 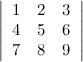 Решение.
Решение. 
 Ответ.
Ответ. 
|
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
| Пример | Задание. Вычислить определитель 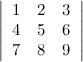 Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель, равный данному.
Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель, равный данному.

 Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ.
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. 
|
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение к треугольному виду, либо с помощью теоремы Лапласа.
· Разложение определителя по элементам строки или столбца
| Пример | Задание. Вычислить определитель  , разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно выполним элементарные преобразования над строками определителя, сделав как можно больше нулей либо в строке, либо в столбце. Для этого вначале
от первой строки отнимем девять третьих,
от второй - пять третьих
и от четвертой - три третьих строки, получаем: , разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно выполним элементарные преобразования над строками определителя, сделав как можно больше нулей либо в строке, либо в столбце. Для этого вначале
от первой строки отнимем девять третьих,
от второй - пять третьих
и от четвертой - три третьих строки, получаем:
 *в решении ошибка, вместо: 9-1 должно быть 9-9 (первая строка после знака «=»
Полученный определитель разложим по элементам первого столбца:
*в решении ошибка, вместо: 9-1 должно быть 9-9 (первая строка после знака «=»
Полученный определитель разложим по элементам первого столбца:
 Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули, например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей - вторую:
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули, например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей - вторую:

 Ответ.
Ответ. 
|
· ПРИВЕДЕНИЕ ОПРЕДЕЛИТЕЛЯ К ТРЕУГОЛЬНОМУ ВИДУ
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его значение, согласно свойствам определителя, равно произведению элементов, стоящих на главной диагонали.
| Пример | Задание. Вычислить определитель  приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент 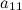 будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный: будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:
 Далее получим нули в первом столбце, кроме элемента
Далее получим нули в первом столбце, кроме элемента 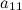 , для этого
из третьей строки вычтем две первых,
а к четвертой строке прибавим первую,
будем иметь: , для этого
из третьей строки вычтем две первых,
а к четвертой строке прибавим первую,
будем иметь:
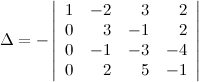 Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если диагональный элемент будет равен
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если диагональный элемент будет равен  , то вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на противоположный знак определителя): , то вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на противоположный знак определителя):
 Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых,
а к четвертой - две вторых строки, получаем:
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых,
а к четвертой - две вторых строки, получаем:
 Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого
к последней строке прибавляем третью:
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого
к последней строке прибавляем третью:

 Ответ.
Ответ. 
|
· Теорема Лапласа
| Теорема | Пусть  - определитель - определитель  -го порядка. Выберем в нем произвольные -го порядка. Выберем в нем произвольные  строк (или столбцов), причем строк (или столбцов), причем  . Тогда сумма произведений всех миноров . Тогда сумма произведений всех миноров  -го порядка, которые содержатся в выбранных -го порядка, которые содержатся в выбранных  строках (столбцах), на их алгебраические дополнения равна определителю. строках (столбцах), на их алгебраические дополнения равна определителю.
|
| Пример | Задание. Используя теорему Лапласа, вычислить определитель  Решение. Выберем в данном определителе пятого порядка две строки - вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
Решение. Выберем в данном определителе пятого порядка две строки - вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):


 Ответ.
Ответ. 
|
· СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ:
1. При транспонировании квадратной матрицы её определитель не меняется: 
| Пример | Известно, что определитель матрицы  равен 3. Тогда определитель матрицы равен 3. Тогда определитель матрицы  , которая равна , которая равна  , также равен 3. , также равен 3.
|
2. Общий множитель в строке можно выносить за знак определителя.
| Пример | 
|
3. 
То есть, если квадратная матрица 
 -го порядка умножается на некоторое ненулевое число
-го порядка умножается на некоторое ненулевое число  , то определитель полученной матрицы равен произведению определителя исходной матрицы
, то определитель полученной матрицы равен произведению определителя исходной матрицы  на число
на число  в степени, равной порядку матриц.
в степени, равной порядку матриц.
| Пример | Задание. Пусть определитель матрицы  третьего порядка равен 3, вычислить определитель матрицы третьего порядка равен 3, вычислить определитель матрицы  .
Решение. По свойству .
Решение. По свойству  Ответ.
Ответ. 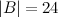
|
4. Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.

5. Если две строки определителя поменять местами, то определитель поменяет знак.
| Пример | 
|
6. Определитель с двумя равными строками равен нулю.
| Пример | 
|
7. Определитель с двумя пропорциональными строками равен нулю.
| Пример | 
|
8. Определитель, содержащий нулевую строку, равен нулю.
| Пример | 
|
9. Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.
| Пример | Пусть задан определитель третьего порядка 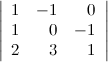 . Прибавим ко второй строке определителя третью его строку, при этом значение определителя не измениться: . Прибавим ко второй строке определителя третью его строку, при этом значение определителя не измениться:
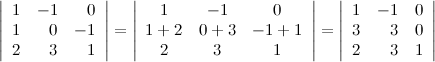
|
10. Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
| Пример | 
|
11. Определитель произведения матриц равен произведению определителей: 