Задачи по теме: « Четырехугольники»

Домашняя самостоятельная работа по ФАЗЕ ЗАПУСКА 9 КЛАСС

Задачи по теме «Окружность»

 

1. Четырехугольник КРМЕ вписан в окружность. Угол Р в 2 раза больше угла Е. Найдите углы Е и Р, если 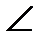К=50⁰, 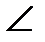М=130⁰.

2. В четырехугольник АВСD вписана окружность. Сторона АВ в 3 раза больше стороны СD. Найдите стороны АВ и СD, если ВС = 13 см, АD = 15 см.

3. АВ и АС – отрезки касательных, проведенных к окружности радиуса 9 см (Рис.1). Найдите длины отрезков АС и АО, если АВ = 12 см.

1. MN и MK – отрезки касательных, проведенных к окружности радиуса 5 см (Рис.2). Найдите длины отрезков MN и MK, если MO = 13 см.

5. Рис.3 Дано: , 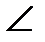СОА=130⁰. Найти: .

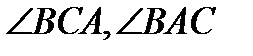1. Рис.4 Дано: , 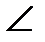CAB=60⁰. Найти: .

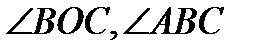7. Хорды MN и РК пересекаются в точке Е так, что МЕ=12 см, NE=3 см, РЕ=КЕ. Найдите РК.

1. Хорды AB и CD пересекаются в точке F так, что AF = 4 см, BF = 16 см, CF=DF. Найдите CD.

9. Начертите треугольник и впишите в него окружность.

10. Начертите треугольник и постройте описанную окружность.

А

В

С

О

Рис. 1

M

K

N

О

Рис. 2

С

Рис. 4

B

A

О

С

Рис. 3

А

В

О

 

 

Задачи по теме: «Площадь»

 

1. Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника.

1. Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше стороны. Найдите площадь треугольника.

3. Катеты прямоугольного треугольника равны 6 и 8 см. Найдите гипотенузу и площадь треугольника.

1. Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и площадь треугольника.

5. Найдите площадь и периметр ромба, если его диагонали равны 8 и 10 см.

6. В прямоугольном треугольнике АВС 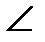С = 90⁰, CD – высота, AD = 18 см, DB=25 см. Найдите СD, АС, ВС.

7. В прямоугольной трапеции АВСК большая боковая сторона равна 3см, угол К равен 45⁰, а высота СН делит основание АК пополам. Найдите площадь трапеции.

8. В прямоугольной трапеции АВСЕ большая боковая сторона равна 8 см, угол А равен 60⁰, а высота ВН делит основание АЕ пополам. Найдите площадь трапеции.

 

Задачи по теме «Подобие треугольников»

1. Рис.1 Дано: 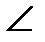А= 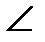В, СО=4, DO=6, AO=5. Найти: ОВ.

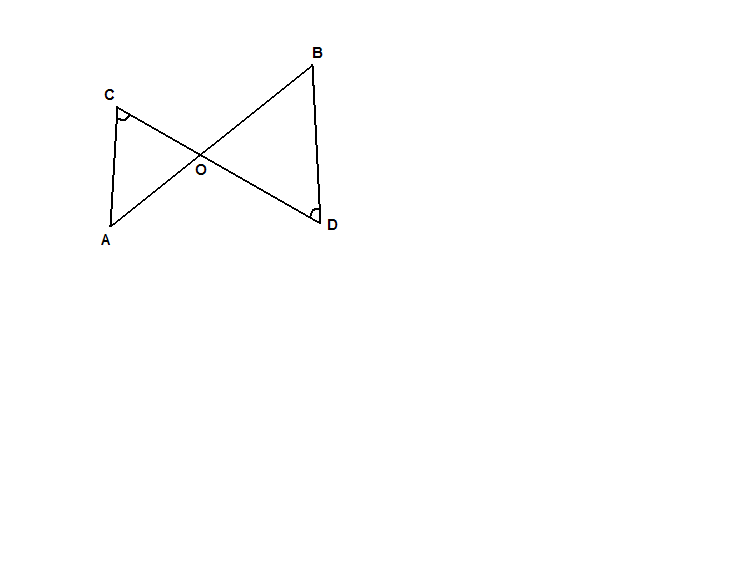
1. Рис.2. Дано: 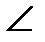С= 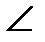D, AО=8, BO=12, CO=6. Найти: ОD.

3.

Рис. 1

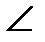В треугольнике АВС АВ=4см, ВС=7см, АС=6см, а в треугольнике MNK MK=8см, MN=12см, KN=14см. Найдите углы треугольника MNK, если А=80⁰, 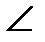В=60⁰.

1. В треугольнике АВС АВ=12см, ВС=18см, 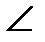В=70⁰, а в треугольнике MNK, MN=6см, KN=9см, 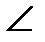N=70⁰. Найдите сторону АС и угол С треугольника АВС, если MK=7см,

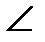K=60⁰.

5.

Рис.2

Даны стороны треугольников PQR и АВС: PQ=16cм, QR=20см, PR=28см и АВ=12см, ВС=15см, АС=21см. Найдите отношение площадей этих треугольников.

1. Найдите отношение площадей треугольников АВС и KMN, если АВ=8см, ВС=12см, АС=16см и КМ=10cм, MN=15см, NK=20см.

 

 

Задачи по теме: «Четырехугольники»

1. Периметр параллелограмма равен 46 см. Найдите стороны параллелограмма, если сумма трех его сторон равна 42 см.

2. Периметр параллелограмма равен 56 см. Найдите стороны параллелограмма, если сумма двух его сторон равна 20 см.

3. Сумма двух углов параллелограмма равна 84⁰. Найдите углы параллелограмма.

4. Сумма трех углов параллелограмма равна 254⁰. Найдите углы параллелограмма.

5. В параллелограмме АВСД О– точка пересечения диагоналей. ВД = 12см, АД = 8см, АО = 7см. Найдите периметр треугольника ВОС.

6. В параллелограмме АВСД О– точка пересечения диагоналей. СД = 15см, АС = 24см, ДО = 9см. Найдите периметр треугольника АОВ.

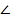7. Рис.1 Дано: АВСД – прямоугольник, АВД = 48⁰. Найдите: СОД, САД.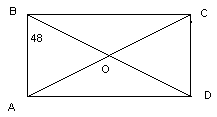

Рис. 1

8. Рис.2 Дано: АВСД – прямоугольник, АОВ= 36⁰. Найдите: САД, ВДС.

Рис. 2