Распространение тепла в стержне конечной длины. Решение некоторых краевых задач линейной теплопроводности методом Фурье
Проведем решение общей первой краевой задачи методом Фурье. Этот метод был рассмотрен достаточно подробно при решении краевых задач для гиперболических уравнений. Схема применения его к уравнениям параболического типа остается прежней. Интересующее нас решение будет получено на основе решений вспомогательных задач – частных случаев указанной задачи.
Однородное уравнение теплопроводности
Пусть однородный стержень длины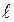 
теплоизолирован по всей длине, причем в нем нет источников тепла. На концах этого стержня поддерживается постоянная или меняющаяся с течением времени температура. Начальное распределение температуры в стержне известно.
А. Распространение тепла в стержне, концы которого
Поддерживаются при нулевой температуре
Задача состоит в отыскании решения однородного уравнения теплопроводности
| (1.193) |
при граничных условиях
 , 
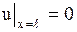
| (1.194) |
и начальном условии
 .
| (1.195) |
Для непрерывности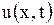 
в точках 
и 
необходимо потребовать, чтобы
 .
| (1.196) |
Согласно методу Фурье ищем частные решения уравнения (1.193), удовлетворяющие граничным условиям (1.194), в виде
 .
| (1.197) |
Подставляя (1.197) в (1.193), имеем
.
Разделение переменных дает
, 
,
откуда получаем два уравнения:
 ,
| (1.198) |
 .
| (1.199) |
Из граничных условий (1.194) имеем
 ,  .
| (1.200) |
Чтобы получить нетривиальное решение уравнения (1.193) вида (1.197), необходимо найти нетривиальное решение уравнения (1.199), удовлетворяющее условиям (1.200). Таким образом, для определения функций 
мы пришли к задаче Штурма – Лиувилля (задаче о собственных значениях), которая исследовалась в задаче о свободных колебаниях ограниченной струны (п.1.28). Там было установлено, что для значений параметра 
, равных
,
существуют нетривиальные решения задачи (1.199) – (1.200):
 .
| (1.201) |
Подставляя значения 
в (1.198), получим уравнение
,
общее решение которого есть
,
где 
- произвольные постоянные.
Таким образом, уравнению (1.196) и граничным условиям (1.197) удовлетворяют функции
, 
при любых . Мы получили множество решений, сумма которых также будет решением уравнения (1.193) (в силу его линейности), удовлетворяющим условию (3.15). Составим формально ряд
 .
| (1.202) |
Функция 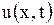в виде (1.202) удовлетворяет граничным условиям, т.к. им удовлетворяют все члены ряда. Требуя выполнения начального условия (1.195), получаем
.
Написанный ряд представляет собой разложение заданной функции 
в ряд Фурье по синусам в промежутке 
. Коэффициенты определяются по известной формуле
 .
| (1.203) |
Итак, решением задачи (1.193) – (1.195) является функция 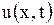, представленная рядом (1.202), коэффициенты которого определяются по формулам (1.203).
Б. Распространение тепла в стержне, на концах которого
поддерживается меняющаяся с течением времени температура
Задача сводится к решению уравнения (1.193) при граничных условиях
 ,  ,
| (1.204) |
и начальном условии
| ,
| (1.205) |
где 
, 
, - заданные функции. Будем искать решение этой задачи в виде ряда Фурье по собственным функциям (1.201)
 ,
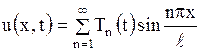| (1.206) |
где
 ,
| (1.207) |
считая при этом 
параметром. Возьмем этот интеграл по частям дважды:
Последний интеграл берем по частям, положив 
, 
. Тогда 
, 
.
Поэтому имеем
.
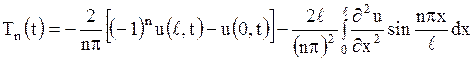Так как 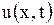удовлетворяет уравнению (1.193) и граничным условиям (1.204), то
 .
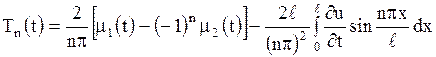| (1.208) |
Дифференцируя теперь выражение (1.207) по , найдем
 .
| (1.209) |
Исключая интеграл из равенства (1.208) и (1.209), получим следующее уравнение для определения коэффициентов 
разложения (1.206):
 .
| (1.210) |
Решим это уравнение методом вариации произвольной постоянной
Тогда
.
Подставляя найденные выражения и 
в линейное неоднородное уравнение (1.210), получим дифференциальное уравнение относительно 
:
,
откуда
.
Интегрируя, находим
.
Таким образом, общее решение уравнения (1.210) имеет вид
 .
| (1.212) |
Определим постоянные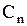 
. Очевидно, 
.
Чтобы удовлетворить начальному условию (1.205), потребуем выполнения равенства
и, следовательно,
 .
| (1.213) |
Итак, решением задачи (1.193), (1.204) – (1.205) является ряд (1.206), в котором функции определяется равенствами (1.212) и (1.213).