Постановка основных краевых задач для уравнений
Лапласа и Пуассона
Для решения уравнения Лапласа или Пуассона, как и вообще для решений стационарных задач, естественно, не задается начальный режим. Задаются лишь условия на границе области.
Математически задача для уравнений Лапласа (Пуассона) ставится так: найти функцию 
, удовлетворяющую внутри области 
, ограниченной замкнутой поверхностью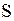 
, уравнению
(
)
и граничному условию, которое может быть взято в одном из следующих видов:
I. 
(граничное условие 1-го рода);
II. 
(граничное условие 2-го рода);
III. 
(граничное условие 3-го рода),
где 
, 
, 
- заданные непрерывные функции;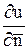 
- производная по внешней нормали 
к поверхности ; 
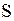- текущая точка поверхности.
Как отмечалось в п. 1.32, задача интегрирования уравнения Лапласа с граничным условием первого рода называется первой граничной задачей или задачей Дирихле, а с условием второго рода – второй граничной задачей или задачей Неймана. Если задана линейная комбинация неизвестной функции и ее нормальной производной, то задачу интегрирования называют третьей граничной задачей. В некоторых задачах на разных участках границы задаются условия разных типов, тогда говорят о смешанной граничной задаче.
В частности, если уравнение Лапласа описывает установившийся режим фильтрации, а функция 
определяет давление в каждой точке пласта, то граничное условие первого рода означает, что в точках поверхности 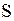задается давление (например, давление на забое скважины или на контуре питания при плоско-параллельном течении); задание граничного условия второго рода равносильно заданию потока фильтрующейся жидкости, т.е. дебита в каждой точке границы . Граничное условие третьего рода задается, когда имеет место переток жидкости в выше – или нижележащие пласты.
Если решение ищется в области , внутренней (или внешней) по отношению к поверхности , то соответствующую задачу называют внутренней (или внешней) граничной задачей.
Решение краевых (граничных) задач для простейших
областей методом разделения переменных
Для областей произвольной формы метод Фурье для решения уравнения Лапласа (или Пуассона) неприменим. Этот метод для уравнения Лапласа проходит лишь в случае некоторых простейших областей, где возможно разделение переменных в граничных условиях (прямоугольник, круг, кольцо, сектор, шар, цилиндр и др.) Получающиеся при этом задачи на собственные значения (задачи Штурма-Лиувилля) приводят к различным специальным функциям. Мы рассмотрим задачи Дирихле в плоской области, при решении которых используются только тригонометрические функции (круговые и гиперболические).
1.38.1. Решение задачи Дирихле (внутренней и внешней) для круга. Интеграл Пуассона
Прежде напомним определение: функция называется гармонической в некоторой области 
, если она непрерывна в этой области вместе со своими частными производными до второго порядка включительно и удовлетворяет уравнению Лапласа в этой области. Решим первую граничную задачу (внутреннюю и внешнюю) для круга. Имея в виду, что различные физические процессы с математической точки зрения могут быть совершенно подобными, мы не будем интерпретировать рассматриваемую задачу в терминах того или иного физического явления, а ограничимся математической постановкой и разберем метод решения, единый для аналогичных проблем.
Внутренняя задача Дирихле: найти функцию , удовлетворяющую уравнению
|
| (1.260) |
внутри круга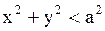 
, непрерывную в замкнутой области 
и принимающую заданные значения на границе круга:
 .
| (1.261) |
Внешняя задача Дирихле: найти функцию, гармоническую в области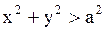 
(внешность круга), ограниченную в области 
и удовлетворяющую граничному условию (1.261).
Обе задачи будем решать одновременно. Задачу проще решать в полярной системе координат 
, где
 ,  .
| (1.262) |
После замены переменных (1.262) уравнение Лапласа
в полярных координатах принимает вид
 .
| (1.263) |
(Читателю предоставляется выполнить это самостоятельно). Соответственно граничное условие (1.262) запишется так:
 ,  .
| (1.264) |
Причем 
, т.к. увеличение 
на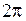 
возвращает точку в исходное положение.
Согласно методу Фурье ищем решение уравнения (1.263) при условии (1.264) в виде
 .
| (1.265) |
Подставляя (1.265) в (1.263), получим
.
Разделяем переменные
.
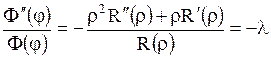Поскольку по обе стороны знака равенства стоят функции от различных независимых переменных, то такое равенство возможно только тогда, когда обе части равны одной и той же постоянной, которую обозначим через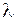 
. Тогда приходим к двум обыкновенным дифференциальным уравнениям:
 ,
| (1.266) |
 .
| (1.267) |
Общее решение линейного уравнения (1.267) есть
 .
| (1.268) |
При изменении угла на величину 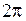однозначная функция 
, как и ограниченная функция 
, должна вернуться к исходному значению, т.е. должно быть выполнено условие периодичности:
.
Отсюда следует, что функция 
является периодической с периодом :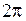
 .
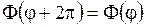| (1.269) |
Решение (1.268) будет удовлетворять условию периодичности лишь тогда, когда 
, где 
Отрицательные 
можно отбросить, т.к. знак 
влияет только на знак произвольной постоянной 
. Значит, отрицательные не дают новых решений.
Таким образом, собственные числа и собственные функции задачи (1.268), (1.269) есть
 ,  , 
| (1.270) |
Подставим теперь в уравнение (1.266):
 .
| (1.271) |
В литературе уравнение (1.271) известно под названием уравнения Эйлера. Его решение ищут в виде
 .
| (1.272) |
Подставляя (1.272) в (1.271), найдем
или, сокращая на 
,
, откуда 
.
Таким образом, для каждого значения 
имеется два линейно независимых решения 
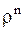и 
, которые определяют свое общее решение 
уравнения (1.271):
 ,
| (1.273) |
где 
- постоянные. Перемножая теперь и 
, согласно (1.265), получим дискретную совокупность функций
 .
| (1.274) |
Для внутренней задачи Дирихле надо положить 
, т.к. если 
, то функция (1.274) обращается в бесконечность при 
и не является гармонической внутри круга 
. Для решения внешней задачи, наоборот, надо взять 
, иначе, положить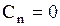 
, т.к. решение (1.274) должно быть ограниченным в области 
. Тогда частными решениями уравнения (1.263) являются функции
для 
,
для ,
.
(Постоянные 
и 
включены в 
и 
). В силу линейности и однородности уравнения Лапласа суммы частных решений
 , ,
| (1.275) |
 ,
| (1.276) |
также будут решением уравнения Лапласа (при условии сходимости рядов).
Подберем произвольные постоянные и так, чтобы удовлетворялось условие (1.264)
 , .
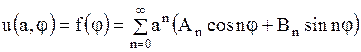| (1.277) |
Напишем ряд Фурье для периодической функции на отрезке 
:
 ,
| (1.278) |
где
,
 ,
| (1.279) |
.
Сопоставляя (1.277) и (1.278), заключаем, что для выполнения граничного условия (1.277) нужно положить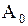 
, 
, 
равными коэффициентам Фурье:
, 
, 
.
Следовательно, для внутренней задачи
, 
, 
,
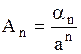для внешней задачи
, 
, 
.
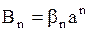Таким образом, решение внутренней задачи Дирихле для круга представим в виде ряда
 ,
| (1.280) |
а решение внешней задачи Дирихле в виде ряда
 ,
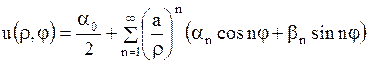| (1.281) |
где 
, 
, 
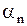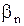определяются как коэффициенты ряда Фурье для функции по формулам (1.279).
Установлено, что так построенные функции (1.280) и (1.281) удовлетворяют всем условиям задачи.
Преобразуем формулы (1.280), (1.281) к более простому виду. Рассмотрим подробно внутреннюю задачу, а для внешней задачи получим результат по аналогии. Преобразуем ряд (1.280), подставив выражения для коэффициентов Фурье (1.279) и произведя затем перестановку порядка суммирования и интегрирования
Произведем тождественные преобразования в фигурных скобках, обозначив для краткости 
, 
; при этом воспользуемся формулой
,
Ряд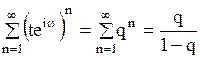 
является бесконечной геометрической прогрессией со знаменателем 
, модуль которого 
. В силу этого имеем следующее представление:
Подставляя полученный результат в (1.282), получаем
 .
| (1.283) |
Эта формула называется формулой Пуассона, а интеграл справа – интегралом Пуассона. Формула (1.283) позволяет записать искомое решение внутренней задачи Дирихле в форме интеграла, зависящего от параметров и 
. Он существует для всех значений и , 
и удовлетворяет уравнению (1.263), а также граничному условию (1.264). Заметим, однако, что интеграл (1.283) теряет смысл при 
. Когда говорят, что функция (1.283) удовлетворяет граничному условию, то под этим подразумевают, что 
. Поэтому решение внутренней задачи записывается так:
  
| (1.284) |
По аналогии решение внешней задачи имеет вид
 
| (1.285) |
Замечание. Интеграл Пуассона дает решение плоской задачи Дирихле для круга. Но он может служить решением и пространственной задачи Дирихле в случае цилиндрической симметрии области, т.е. когда область есть бесконечный цилиндр, а искомая функция 
, например, температура или электрический потенциал, не зависит от 
. Тогда температура или потенциал в любом сечении, перпендикулярном к оси 
, зависит только от и . Следовательно, здесь имеет место плоская задача Дирихле.