| 4,23 | 4,32 | 4,32 | 4,33 | 4,35 | 4,40 | 4,41 | 4,43 | 4,45 | 4,45 |
| 4,46 | 4,47 | 4,51 | 4,53 | 4,55 | 4,56 | 4,58 | 4,58 | 4,59 | 4,60 |
| 4,61 | 4,61 | 4,62 | 4,63 | 4,65 | 4,65 | 4,69 | 4,69 | 4,72 | 4,73 |
| 4,73 | 4,75 | 4,77 | 4,78 | 4,78 | 4,78 | 4,80 | 4,80 | 4,81 | 4,85 |
| 4,86 | 4,86 | 4,87 | 4,87 | 4,88 | 4,89 | 4,91 | 4,98 | 5,01 | 5,17 |
При построении гистограммы на оси абсцисс гистограммы указывают значения параметра от y min до y max, полученные в результате построения статистического ряда. Затем на этой же оси оси откладывают k интервалов, как показано на рис. 1.2. Количество интервалов рассчитывается по формуле
k » 3,3lg N, (1.14)
где N – число измеренных значений параметра y. Значение числа k округляется до ближайшего целого числа.
Для N =50 получим k =3,3·lg50=3,3·1,7=5,6. Округляя до ближайшего целого числа, выбираем число интервалов k =6.
Длина интервала D k рассчитывается из выражения
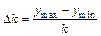 , (1.15)
, (1.15)
где y maxи y min– максимальное и минимальное значения параметра у.
Максимальное и минимальное значения сопротивления Ri из таблицы 1.2: R min=4,23 кОм, R max=5,17 кОм. Согласно формуле (1.15) рассчитываем длину интервала D k:
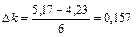 кОм.
кОм.
Рассчитываем граничные значения сопротивлений резисторов R min j и R max j, входящих в j –й интервал, результаты заносим в столбцы 2 и 3 таблицы 1.3. По таблице 1.2 подсчитываем число попаданий nj параметра Rj в заданный интервал D kj, результаты заносим в столбец 4 таблицы 1.3.
Таблица 1.3
| Номер интервала, j | R min j , кОм | R max j , кОм | Количество значений nj в интервале j | Частость, pj | R ср j |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 4,23 | 4,38 | 0,1 | 4,21 | ||
| 4,38 | 4,54 | 0,18 | 4,37 | ||
| 4,54 | 4,70 | 0,28 | 4,54 | ||
| 4,70 | 4,85 | 0,22 | 4,71 | ||
| 4,85 | 5,01 | 0,20 | 4,87 | ||
| 5,01 | 5,17 | 0,02 | 5,04 |
Значения относительных частот (частостей) определяются по формуле
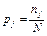 , (1.16)
, (1.16)
где nj – число попаданий значений параметра yj в заданный интервал D kj;
 - общее число измеренных значений параметра y.
- общее число измеренных значений параметра y.
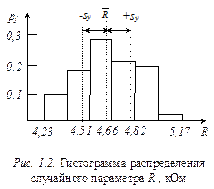 Результаты определения частостей pj по формуле (1.16) заносим в столбец 5 таблицы 1.3.
Результаты определения частостей pj по формуле (1.16) заносим в столбец 5 таблицы 1.3.
В столбец 6 таблицы 1.3. заносим значения сопротивления R ср j, соответствующие середине j -го интервала.
На вертикальной оси гистограммы (рис. 1.2) откладываются значения относительных частот (частостей) рj появления значений параметра у в заданных интервалах D kj. Затем на каждом интервале D k, как на основании, строятся прямоугольники, высота которых пропорциональна частости pj данного интервала.
Среднее значение параметра 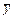 рассчитывается по формуле
рассчитывается по формуле
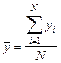 =4,66 кОм. (1.17)
=4,66 кОм. (1.17)
При работе с выборками конечного объема для оценки отклонения среднего значения параметра 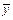 пользуются понятием выборочного среднеквадратического отклонения sy.
пользуются понятием выборочного среднеквадратического отклонения sy.
Выборочное среднеквадратическое отклонение sy определяется из выражения
 =0,154 кОм. (1.18)
=0,154 кОм. (1.18)
В предположении о нормальном законе распределения относительное предельное отклонение параметра d у под влиянием дестабилизирующих факторов рассчитывается из соотношения
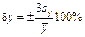 ≈ 9,9 %. (1.19)
≈ 9,9 %. (1.19)
Пример 1.7. Рассчитать относительное отклонение d L индуктивности L высокочастотной катушки индуктивности.
Решение. Воспользуемся выражением для индуктивности L однослойной катушки: L = L o DN 2×10–3, мкГ. Входными параметрами являются L o, D, N.
Рассчитываем коэффициенты влияния Bi:
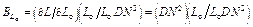 = 1,
= 1,
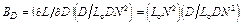 = 1,
= 1,
 = 2.
= 2.
Определяем относительные отклонения d xi входных параметров. Для этого, например, из чертежа катушки находим, что допуск D D на величину диаметра катушки D = 10 мм равен  0,1 мм, следовательно, d D = 0,01. При числе витков катушки N = 10 за технологическую погрешность намотки примем, например, 0,2 витка, следовательно, d N = 0,02.
0,1 мм, следовательно, d D = 0,01. При числе витков катушки N = 10 за технологическую погрешность намотки примем, например, 0,2 витка, следовательно, d N = 0,02.
Для расчета относительного отклонения d L o параметра L o учитываем, что L o = j(l / D), где l – длина намотки катушки. С целью упрощения полагаем, что функция j(l / D) = k (l / D), где k – коэффициент. Рассчитываем коэффициенты влияния Bi для функции k (l / D):
 = 1,
= 1,
 = –1.
= –1.
Принимаем d l = d D = 0,01. По формуле (1.6) рассчитываем d L o = | Вl |d l + | ВD |d D = 1×0,01 + |–1|×0,01 = 0,02.
Ответ: d L = | ВL o|d L o + | ВD |d D + | ВN |d N = 1×0,02 + 1×0,01 + 2×0,02 = 0,07.
Таким образом, относительная производственная погрешность индуктивности высокочастотной катушки при заданных отклонениях входных параметров составляет 0,07 (7%). Если этот результат не устраивает заказчика (допустим, по ТЗ требуется обеспечить относительную погрешность индуктивности 2%), то разработчик должен предусмотреть меры по уменьшению допусков на входные параметры, в данном случае на геометрические размеры катушки и точность технологического процесса намотки.
Пример 1.8. Рассчитать требования к производственным допускам на удельное сопротивление обмоточного провода и размеры каркаса проволочного резистора со следующими параметрами:
1) номинальное сопротивление R н = 5100  5 Ом;
5 Ом;
2) материал провода – константан (сплав МНМц40-1,5, r = 0,48×10–6 Ом×м).
3) диаметр обмоточного провода d 0=0, 12 мм;
4) диаметр каркаса D к=33,5 мм.
Решение.
1. Расчет производственной погрешности сопротивления резистора d R н. Применяем вероятностно-статистический метод анализа точности параметров радиокомпонентов.
Для расчета производственной погрешности сопротивления резистора используем формулу для сопротивления проволочного резистора:
 . (1.20)
. (1.20)
Подставляя в эту формулу значение l пр = N p D к, получим:
 . (1.21)
. (1.21)
Из выражения (1.21) следует, что относительное среднеквадратическое отклонение сопротивления резистора 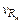 зависит от нескольких факторов: среднеквадратического отклонения удельного сопротивления провода v r, отклонений диаметра провода
зависит от нескольких факторов: среднеквадратического отклонения удельного сопротивления провода v r, отклонений диаметра провода 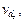 диаметра каркаса
диаметра каркаса 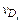 и числа витков vN. Пренебрегая последним фактором, согласно формуле (1.21) рассчитаем относительные коэффициенты влияния B r =1,
и числа витков vN. Пренебрегая последним фактором, согласно формуле (1.21) рассчитаем относительные коэффициенты влияния B r =1,  = –2,
= –2,  = 1. Таким образом, относительное среднеквадратическое отклонение сопротивления проволочного резистора равно
= 1. Таким образом, относительное среднеквадратическое отклонение сопротивления проволочного резистора равно
 . (1.22)
. (1.22)
Полагая, что погрешности входных параметров распределены по нормальному закону, для производственной погрешности сопротивления проволочного резистора получим следующее выражение:
d R н, % =  3
3 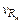 , %. (1.23)
, %. (1.23)
Поскольку в исходных данных к расчету заданы требования на предельное допускаемое отклонение сопротивления резистора d R н = 5/5100 = 0,001, то в данном случае следует решать обратную задачу расчета производственных допусков (задачу синтеза): по заданному допуску на выходной параметр d R н  3
3 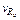 подобрать требуемые значения допусков на входные параметры, к которым относятся предельные отклонения удельного сопротивления провода dr
подобрать требуемые значения допусков на входные параметры, к которым относятся предельные отклонения удельного сопротивления провода dr  3 v r, диаметра провода d d o
3 v r, диаметра провода d d o  3
3 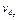 , диаметра каркаса d D к
, диаметра каркаса d D к 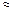 3
3 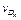 , где
, где 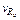 , v r,
, v r, 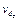 ,
,  являются среднеквадратическими отклонениями соответствующих параметров.
являются среднеквадратическими отклонениями соответствующих параметров.
2. Для приближенного решения этой задачи, полагая равными вклады каждого из отклонений входных параметров в общую погрешность, формулу (1.24) представим в виде
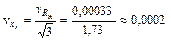 ,
,
где 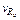 = 0,001/3
= 0,001/3  0,00033;
0,00033; 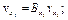 vxi– относительноесреднеквадратическое отклонение i -го входного параметра, 3 – число входных параметров.
vxi– относительноесреднеквадратическое отклонение i -го входного параметра, 3 – число входных параметров.
3. Для того, чтобы максимальное отклонение сопротивления резистора d R н находилось в заданных пределах, необходимо применять для изготовления РЭ провод с относительным отклонением удельного сопротивления dr, не превышающим 0,0002×3 = 0,0006, т.е. 0,06%; такое же относительное отклонение должен иметь диаметр каркаса d D к. Предельное отклонение диаметра провода намотки без изоляции d d o не должно превышать величины 0,0002×3/2 = 0,0003 или 0,03%.
Абсолютные значения допусков:
Dr=0,0006× 0,48×10–6=0,3×10–9 Ом×м;
D d o =0,0003× 0,145=0,4×10–4 мм=0,04 мкм;
D D к =0,0006× 33,5=0,02 мм=20 мкм.
Обеспечение указанных допусков из-за их малых величин технически сложно. Поэтому целесообразно получить заданную величину d R н методом подгонки длины провода намотки в пределах 0,001×105,2 м 
 0,105 м.
0,105 м.
Ответ:
1) относительные отклонения dr=0,06%; d d o=0,03%; D к=0,06%;
2) абсолютные отклонения Dr=0,3×10–9 Ом×м;D d o=0,04 мкм; D D к=20 мкм;
Пример 1.9. Рассчитать производственную погрешность d L c индуктивности катушки с броневым сердечником при следующих исходных данных:
1) броневой сердечник типоразмера Б11;
2) габаритные размеры сердечника (рис. 4.11):
наружный диаметр D 1 = 11 мм,
внутренний диаметр D 2 = 9,4 мм,
диаметр центрального керна D 3 = 4,7 мм,
высота сердечника H 1 = 6,4 мм,
высота окна H 2 = 4,4 мм;
3) начальная магнитная проницаемость сердечника mн = 45  18%;
18%;
4) относительная магнитная проницаемость сердечника mотн = 38,8.
5) величина зазора между чашками l з = 0,2 мм  30%.
30%.
Решение.
Для расчета производственного отклонения индуктивности катушки d L н используем вероятностно-статистический метод анализа точности параметров радиокомпонентов.
С этой целью воспользуемся формулой (4.22) для индуктивности катушки с броневым сердечником, которую представим в виде
 , мкГ, (1.24)
, мкГ, (1.24)
где mн – начальная магнитная проницаемость материала сердечника; l c – длина магнитной силовой линии, см; l з – величина зазора между половинками сердечника, см.
Если пренебречь малыми отклонениями в числе витков N катушки, в площади поперечного сечения броневого сердечника S c и длине магнитной силовой линии l c, то выражение (1.24) можно представить следующим образом:
 , (1.25)
, (1.25)
где  – постоянная величина.
– постоянная величина.
Из (1.25) находим, что относительное среднеквадратическое отклонение индуктивности vL cкатушки на броневом сердечнике рассчитывается по формуле
 . (1.26)
. (1.26)
Рассчитаем значения коэффициентов влияния B mни Bl з:
 =
= 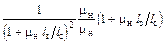 =
= 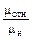 ;
;
(1.27)
 =
=  =
=  .
.
Подставляя значения B mни Bl зв формулу (1.26), получим следующее выражение для расчета относительного среднеквадратического отклонения индуктивности катушки на броневом сердечнике:
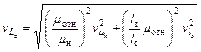 . (1.28)
. (1.28)
Из формулы (1.28) следует, что влияние отклонений начальной магнитной проницаемости mн на относительное отклонение индуктивности катушки 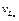 снижается при уменьшении mотн. Но при заданной проницаемости материала уменьшение mотн достигается увеличением зазора l змежду чашками, что в свою очередь ведет к росту коэффициента влияния Bl зперед vl з.
снижается при уменьшении mотн. Но при заданной проницаемости материала уменьшение mотн достигается увеличением зазора l змежду чашками, что в свою очередь ведет к росту коэффициента влияния Bl зперед vl з.
Настройка индуктивности катушки к заданному номиналу осуществляется с помощью сердечника-подстроечника.
При выполнении расчетов производственной погрешности индуктивности катушки значение среднеквадратического отклонения магнитной проницаемости v mн находят в справочниках на магнитные материалы; величина vl зрассчитывается из допусков на размеры броневого сердечника, приведенные в ТУ. Полагая, что погрешности входных параметров распределены по нормальному закону, производственное отклонение индуктивности катушки можно рассчитать по формуле
d L с, % =  3
3 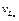 , %.
, %.
1. По формуле (4.20) рассчитываем длину магнитной силовой линии l c:
l c= (H 1 + H 2) + (D 1 – D 3)=
= (6,4 + 4,4) + (11 – 4,7)=17,1 мм.
2. Рассчитываем среднеквадратическое отклонение начальной магнитной проницаемости v mн  0,18/3=0,06 и величины зазора между чашками vl з
0,18/3=0,06 и величины зазора между чашками vl з  0,3/3=0,1.
0,3/3=0,1.
3. Расчет производственной погрешности катушки выполняем по формуле (1.28):
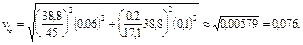
Полагая, что погрешности входных параметров распределены по нормальному закону, производственное отклонение индуктивности катушки равно
d L c = 3×7,6 %  22,8 %.
22,8 %.
Заданную величину d L получают методом подстройки индуктивности с помощью сердечника-подстроечника.
Ответ. d L c = 22,8 %.
Пример 1.10. Рассчитать температурный коэффициент сопротивления (ТКС) проволочного точного резистора, а также диапазон изменения сопротивления резистора в заданном диапазоне температур. Исходные данные для расчета:
1) номинальное сопротивление R н = 5100  5 Ом;
5 Ом;
2) температурный диапазон работы –45¼+40 °C;
3) ТКС материала провода (сплав МНМц40-1,5) ar, T = +0,2×10–4 1/К.
4) температурный коэффициент линейного расширения обмоточного провода (ТКЛР) a d,T = +0,16×10–4 1/К;
5) ТКЛР материала каркаса a D,T = +0,1×10–4 1/К.
Решение.
1. Согласно формуле (1.21) температурный коэффициент сопротивления резистора рассчитывается по формуле
a R,T = ar, T – 2  +
+ 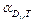 , 1/К. (1.29)
, 1/К. (1.29)
Следовательно, ТКС проволочного резистора зависит от ТКС намоточного провода и ТКЛР материалов провода и каркаса.
Подставляяя значения параметров в формулу (1.28), получим для величины ТКС:
a R,T = (0,2 – 2×0,16 + 0,1)×10–4 = –0,02×10–4 1/К.
2. Значение электросопротивления при минимальной или максимальной температурах эксплуатации рассчитывается по формуле
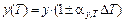 , (1.30)
, (1.30)
где y н– номинальное значение параметра y (в данном случае y – электросопротивления резистора) при комнатной температуре Т о= 20 °С; D T = Т – Т – изменение температуры, К.
В заданном диапазоне температур эксплуатации (–45¼+40 °С) значение сопротивления при минимальной температуре эксплуатации равно
R (–45 °С) = 5100(1 + 0,02×10–4×65) = 5100,6 Ом.
Значение сопротивления при максимальной температуре эксплуатации составит
R (+40 °С)=5100(1–0,02×10–4×20) =5099,7 Ом.
Следовательно, изменение сопротивления резистора в заданном диапазоне температур эксплуатации не превышает +0,6¼–0,3 Ом, и значения сопротивления не выходят за пределы установленного допуска ( 5 Ом).
5 Ом).
Ответ:
1) a R,T =–0,02×10–4 1/К;
2) 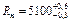 Ом.
Ом.
Пример 1.11. Рассчитать температурный коэффициент индуктивности (ТКИ) и оценить значения индуктивности катушки с броневым сердечником в заданном диапазоне температур при следующих исходных данных:
1) допускаемое отклонения величины индуктивность δ L =  %;
%;
2) материал сердечника - феррит 50ВЧ2;
3) начальная магнитная проницаемость сердечника mн = 45;
4) ТКm=am, T = (–1,3...+4,5)10–4 К–1;
6) диапазон температур эксплуатации (–40¼+40) °С.
Решение.
Согласно формуле (1.25) коэффициенты влияния B mни Bl зиндуктивности катушки с броневым сердечником равны:
 =
= 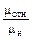 ;
;
 =
=  .
.
Подставляя эти значения в формулу для температурного коэффициента индуктивности катушки с броневым сердечником получаем, что выражение для ТКИ имеет вид
a L,T =  am, T
am, T 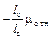
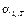 , 1/К. (1.31)
, 1/К. (1.31)
Из (1.31) следует, что величина ТКИ катушки с броневым сердечником определяется значением температурного коэффициента начальной магнитной проницаемости ТК m магнитного сердечника и ТКЛР материала сердечника. Известно, что температурные коэффициенты линейного расширения ферритов и магнитодиэлектриков в сотни раз меньше, чем температурный коэффициент магнитной проницаемости. Поэтому для расчета ТКИ справедливо следующее выражение
a L,T =  am, T =
am, T =  . (1.32)
. (1.32)
Таким образом, температурная стабильность индуктивности катушек на броневых сердечниках определяется не абсолютным температурным коэффициентом проницаемости материала, а его справочным относительным значением am, T /mн 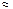 +(0,4¼1)10–6 и требуемым значением магнитной проницаемости сердечника mотн.
+(0,4¼1)10–6 и требуемым значением магнитной проницаемости сердечника mотн.
Значение температурного коэффициента магнитной проницаемости феррита 50ВЧ2 am, T cоставляет в среднем +1,6×10–4 К–1.
1. Расчет ТКИ катушки выполняем по формуле (1.32):
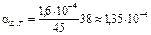 1/К.
1/К.
2. Используя полученное значение ТКИ,оценим изменение индуктивности катушки в заданном диапазоне температур эксплуатации (–40¼+40 °С). Принимаем в качестве нормальной температуру Т о = +20 °С.
Согласно формуле (1.30) значение индуктивности катушки при минимальной температуре эксплуатации составляет
L (–40 °С) = 100(1 – 1,35×10–4×60) = = 99,2 мкГ,
а значение индуктивности при максимальной температуре эксплуатации составит
L (+40 °С) = 100(1 + 1,35×10–4×20) = 100,3 мкГ.
Следовательно, изменение индуктивности катушки в заданном диапазоне температур эксплуатации не превышает (–0,8¼+0,3)%, что соответствует требованиям задачи.
Ответ. a L,T = 1,35×10–4 1/К; L (–40 °С) = 99,2 мкГ; L (+40°С)= 100,3 мкГ.
Пример 1.12. Рассчитать производственную погрешность емкости и температурную нестабильность емкости дискретного конденсатора с параллельным включением конденсаторов по схеме рис. 3.6 при следующих исходных данных:
1) количество ветвей n =4;
2) значения емкостей конденсаторов, включенных в ветви: С1 =0,56 пФ±0,25%; С2 =1,42 пФ±0,25%; С3 =3,20 пФ±0,25%; С4 =6,90 пФ±0,25%;
3) ТКЕ (a C,T) = (0  30)×10–6 К–1
30)×10–6 К–1
4) коэффициент перекрытия контура по частоте kf =1,167;
5) максимальное значение эквивалентной емкости Cэ. max=53,95 пФ;
6) диапазон температур эксплуатации (–60¼+40 °С)
Решение.
1. Относительное среднеквадратическое отклонение емкости дискретного конденсатора 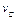 з ависит от отклонений емкости составляющих конденсаторов
з ависит от отклонений емкости составляющих конденсаторов 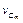 и рассчитывается согласно выражению:
и рассчитывается согласно выражению:
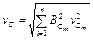 , (1.33)
, (1.33)
где BCm – относительные коэффициенты влияния.
Для расчета коэффициентов влияния BCm используем формулу для емкости параллельно соединенных конденсаторов
 . (1.34)
. (1.34)
Из (1.34) следует, что
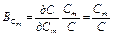 . (1.35)
. (1.35)
Подставляя значение BCm из (1.35) в выражение (1.34) и полагая относительные среднеквадратические отклонения емкостей конденсаторов vCm одинаковыми, получаем для расчета vC следующую формулу:
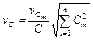 . (1.36)
. (1.36)
Относительное среднеквадратическое отклонение емкости конденсатора vCm рассчитаем по формуле
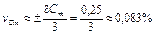 .
.
Суммарная емкость конденсаторов, входящих в контур, равна
С =0,56 +1,42 +3,20+6,90 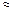 12 пФ
12 пФ
Подставляя в формулу (1.33) значения переменных получим для величины относительного среднеквадратического отклонения емкости ДКПЕ значение
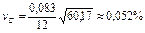 .
.
Производственную погрешность емкости ДКПЕ dС, % рассчитываем по формуле
d С =3· vC =3·0,052=0,16%.
2. Величина температурного коэффициента емкости ДКПЕ рассчитывается по формуле
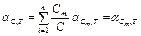 , (1.37)
, (1.37)
где значения ТКЕ a Сm,T составляющих конденсаторов приняты одинаковыми и являются справочными величинами.
Расчет ТКЕ дискретного конденсатора выполняем по формуле (1.37), откуда следует, что
a С,T = (0  30)×10–6 1/К.
30)×10–6 1/К.
Используем максимальное значение ТКЕ ( 30×10–6 К–1)для оценки изменения максимальной емкости ДКПЕ С э.max пФ в заданном диапазоне температур эксплуатации (–60¼+40 °С). Принимаем в качестве нормальной температуру Т 0= +20 °С.
30×10–6 К–1)для оценки изменения максимальной емкости ДКПЕ С э.max пФ в заданном диапазоне температур эксплуатации (–60¼+40 °С). Принимаем в качестве нормальной температуру Т 0= +20 °С.
Согласно формуле, которая следует из (1.30):
С (Т)= С (Т 0)[1±a С,T Δ Т ] (1.38)
значение емкости при минимальной температуре эксплуатации составит
С (–60 °С) = 53,95(1 + 30×10–6×80) = 54,08 пФ,
а значение емкости при максимальной температуре эксплуатации составит
С (+40 °С) = 53,95(1 – 30×10–6×20) = 53,98 пФ.
Следовательно, изменение емкости ДКПЕ в заданном диапазоне температур эксплуатации не превышает +0,13¼– 0,03 пФ.
Ответ. d С =0,16%; a С,T = (0  30)×10–6 1/К; С (–60 °С) =54,08 пФ; С (+40 °С) = = 53,98 пФ.
30)×10–6 1/К; С (–60 °С) =54,08 пФ; С (+40 °С) = = 53,98 пФ.
Пример 1.13. Рассчитать среднеквадратическое отклонение 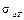 температуры перегрева трансформатора питания и максимальную температуру нагрева Т тр трансформатора при следующих исходных данных:
температуры перегрева трансформатора питания и максимальную температуру нагрева Т тр трансформатора при следующих исходных данных:
1)
| Номер обмотки | Токи в обмотках, А | Диаметры проводов обмоток d 0 i, мм | Сопротивления обмоток ri, Ом |
| 0,351 1,0 0,5 | 0,41 0,62 0,46 | 45,8 0,94 18,1 |
2) температура перегрева D Т =65о С;
3) тепловой коэффициент А = 23,22 К/Вт;
4) тепловой коэффициент Б = 12,15 К/Вт;
5) потери в меди P м=10,67 Вт;
6) потери в стали P с=0,46 Вт;
7) масса магнитопровода М с =0,42 кг;
8) максимальная индукция в магнитопроводе B м=1,6 Т.
Решение.
1. При расчете отклонений температуры перегрева трансформатора питания следует учесть, что температура перегрева D Т трансформатора является случайной величиной. Отклонения температуры перегрева связаны с большим разбросом магнитных характеристик материалов, применяемых для изготовления магнитопроводов, и отклонениями сопротивления провода намотки, возникающими в процессе изготовления трансформатора (в процессе механической и термической обработки магнитопровода и склеивания его половинок, при намотке катушки трансформатора, сопровождающейся вытягиванием провода и т.д.). Количественно разброс температуры перегрева трансформаторов (производственную погрешность) можно выразить через отклонения величин потерь в стали P c и потерь в меди P м с помощью вероятностно-статистического метода анализа точности параметров радиокомпонентов.
При определении производственной погрешности температуры перегрева D Т используем формулу
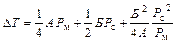 , К. (1.39)
, К. (1.39)
Для расчета среднеквадратического отклонения температуры перегрева s(D Т) воспользуемся выражением (1.11). При этом считаем тепловые коэффициенты А и Б детерминированными величинами, а значения потерь в стали P c и потерь в меди P м– случайными:
 , К, (1.40)
, К, (1.40)
где 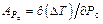 и
и  – коэффициенты влияния потерь в стали и меди на абсолютное отклонение температуры перегрева трансформатора;
– коэффициенты влияния потерь в стали и меди на абсолютное отклонение температуры перегрева трансформатора; 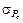 и
и 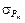 – среднеквадратические отклонения потерь в стали и меди.
– среднеквадратические отклонения потерь в стали и меди.
Коэффициенты влияния 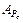 и
и 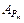 определяютcя в результате дифференцирования выражения (1.39) по соответствующим входным параметрам:
определяютcя в результате дифференцирования выражения (1.39) по соответствующим входным параметрам:
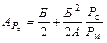 , К/Вт; (1.41а)
, К/Вт; (1.41а)
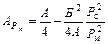 , К/Вт. (1.41б)
, К/Вт. (1.41б)
Подставляя исходные данные задачи в формулы (1.41) получаем следующие значения коэффициентов влияния 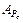 и
и 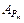 :
:
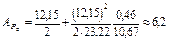 К/Вт;
К/Вт;
 К/Вт.
К/Вт.
2. На основании формулы (5.18) значение среднеквадратического отклонения потерь в стали 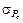 рассчитываем по формуле
рассчитываем по формуле
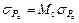 , Вт, (1.42)
, Вт, (1.42)
где М с– масса магнитопровода, кг; 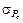 – среднеквадратическое отклонение удельных потерь в стали, Вт/кг.
– среднеквадратическое отклонение удельных потерь в стали, Вт/кг.
Величина среднеквадратического отклонения удельных потерь в стали 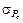 возрастает с увеличением значения максимальной индукции В м в магнитопроводе и определяется по графику зависимости
возрастает с увеличением значения максимальной индукции В м в магнитопроводе и определяется по графику зависимости 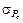 = f (В м), представленному на рис. 1.3, а. Согласно этому графику величина среднеквадратического отклонения удельных потерь в стали
= f (В м), представленному на рис. 1.3, а. Согласно этому графику величина среднеквадратического отклонения удельных потерь в стали 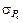 = 0,4 Вт/кг. Следовательно, значение среднеквадратического отклонения потерь в стали равно:
= 0,4 Вт/кг. Следовательно, значение среднеквадратического отклонения потерь в стали равно:
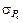 = 0,42×0,4
= 0,42×0,4 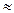 0,17 Вт.
0,17 Вт.

3. Выражение для расчета среднеквадратического отклонения потерь в меди 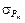 на основании формулы (5.19) имеет следующий вид:
на основании формулы (5.19) имеет следующий вид:
 , Вт, (1.43)
, Вт, (1.43)
где Ii – значение тока i -й обмотки, А; ri – сопротивление i -й обмотки, Ом; 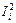 – коэффициент влияния сопротивления i -й обмотки, А2; s ri – среднеквадратическое отклонение сопротивления провода i -й обмотки, Ом.
– коэффициент влияния сопротивления i -й обмотки, А2; s ri – среднеквадратическое отклонение сопротивления провода i -й обмотки, Ом.
Величина относительного среднеквадратического отклонения сопротивления провода намотки s ri / r н i уменьшается с увеличением диаметра провода намотки d из и определяется из графика зависимости s r / r н = f (d из) на рис. 1.3, б. Искомая величина s ri для заданного диаметра провода d из i рассчитывается по формуле
s ri = ri s r / r н. (1.44)
Из графика зависимости s r / r н= f (d из) на рис. 1.3, б для диаметров проводов d из1= 0,41 мм, d из2= 0,62 мм, d из3= 0,46 мм определяем значения s r / r н = 0,035; 0,024 и 0,032, соответственно. Затем по формуле s ri = ri s r / r н, в которой сопротивление первичной обмотки r 1 = 43,93 Ом, сопротивления вторичных обмоток r 2 = 0,91 Ом и r 3 = 17,42 Ом, рассчитываем среднеквадратические отклонения сопротивлений обмоток:
s r 1= 43,93×0,035 = 1,54 Ом;
s r 2= 0,91×0,024 = 0,02 Ом;
s r 3= 17,42×0,032 = 0,56 Ом.
Подставляя рассчитанные значения s ri и значения токов обмоток Ii в формулу (1.52), рассчитываем среднеквадратические отклонения потерь в меди 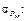
 Вт.
Вт.
5. Подставляя рассчитанные значения коэффициентов влияния и потерь в стали и меди в формулу (1.48), для величины среднеквадратического отклонения температуры перегрева трансформатора имеем
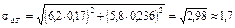 К.
К.
6. Полагая, что погрешности входных параметров распределены по нормальному закону, для расчета максимального значения температуры нагрева трансформатора используется следующее выражение:
Т тр = Т о + D Т + 3 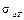 , °С, (1.45)
, °С, (1.45)
где Т о – температура окружающей среды, °С; D Т – расчетное значение температуры перегрева трансформатора.
Для максимальной величины температуры нагрева трансформатора получим следующее значение:
Т тр  35 + 65 + 3×1,7 = 105 °С.
35 + 65 + 3×1,7 = 105 °С.
По значению Т трвыбирается класс нагревостойкости изоляции проводов намотки и других изоляционных материалов, применяемых в конструкции трансформатора. Если же значение температуры перегрева превышает значение, указанное в ТЗ, то следует провести анализ конструкции трансформатора и скорректировать результаты, полученные на первом этапе расчета.
Следовательно, для изоляции проводов намотки и других изоляционных материалов, применяемых в конструкции проектируемого трансформатора, следует выбирать материалы с классом нагревостойкости не ниже А (Т max = 105 °С).
Ответ. 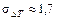 К; Т тр= 105 °С.
К; Т тр= 105 °С.