Для студентов I-го курса,
Осенний семестр 2018/2019 уч.г.
Раздел 1. Последовательности. Функции. Теория пределов. Непрерывность функций одной переменной.
1. Числовые последовательности. Бесконечно малые последовательности, их свойства. Бесконечно большие последовательности, их связь с бесконечно малыми.
1. Числовая последовательность– функция вида y = f (x), x О N,где N – множество натуральных чисел (или функция натурального аргумента), обозначается y = f (n) или y 1, y 2, …, yn. Значения y 1, y 2,…называют соответственно первым, вторым, третьим, … членами последовательности.
2. Последовательность {an} называется бесконечно малой (б.м.), если  , т.е.
, т.е.  .
.
Свойства:
1. Сумма (разность) двух б.м.п. есть б.м.п..
2. Б.м.п. ограничена.
3. Произведение ограниченной последовательности на б.м. есть б.м.п..
4. Если все элементы б.м.п. равны одному и тому же числу, то это число - ноль.
3. Последовательность {xn} называется бесконечно большой (б.б.п.), если для любого  существует номер
существует номер 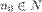 такой, что для любого
такой, что для любого  выполняется неравенство:
выполняется неравенство: 

 Свойства:
Свойства:
1. Сумма б.б.п. одного знака есть б.б.п. того же знака.
2. Сумма б.б. и ограниченной последовательностей есть б.б.п..
3. Произведение б.б.п. есть б.б.п..
4. Произведение б.б.п. на константу есть б.б.п..
Связь б.м.п. с б.б.п.:
1. Если {xn} - б.б.п., то начиная с некоторого номера определена последовательность {1/xn}, причём она является б.м..
2. Если {yn} - б.м.п., то начиная с некоторого номера определена последовательность {1/yn}, причём она является б.б..
2. Конечный предел числовой последовательности.
Точка a (конечная или бесконечно удаленнная) числовой прямой называется пределом последовательности { xn } действительных чисел, если для любого  > 0 существует такой номер
> 0 существует такой номер 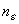 , что для всех номеров n >
, что для всех номеров n >  члены xn содержатся в окрестности U (a;
члены xn содержатся в окрестности U (a;  ): xn
): xn  U (a;
U (a;  ), n >
), n > 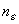 .
.
Если числовая последовательность имеет конечный предел, то она называется сходящейся.
3. Теоремы о пределах суммы, произведения и частного сходящихся последовательностей. Теоремы о пределах последовательностей, связанных неравенствами.
1. 1. Сумма сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен сумме пределов последовательностей {xn} и {yn}.
2. Произведение сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен произведению пределов последовательностей {xn} и {yn}.
3. Частное двух сходящихся последовательностей {xn} и {yn}, предел второй из которых отличен от нуля, определено, начиная с некоторого номера, и представляет собой сходящуюся последовательность, предел которой равен частному пределов последовательностей {xn} и {yn}.
2. 1. Теорема о двух милиционерах. Если  выполняются неравенства
выполняются неравенства  и если
и если 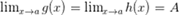 то
то 
 2. Если
2. Если  выполняется неравенство
выполняется неравенство  и если
и если 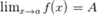 ,
,  , то
, то  .
.
4. Число е, как предел последовательности с общим членом  Последовательность с общим членом
Последовательность с общим членом  имеет конечный предел при х →
имеет конечный предел при х →
5. Конечный предел функции действительного переменного при х → а (а - число или символ ).

6. Бесконечно малые и бесконечно большие функции.
Бесконечно малая - числовая функция или последовательность, которая стремится к нулю.
Бесконечно большая - числовая функция или последовательность, которая стремится к бесконечности определённого знака.
7. Односторонние пределы.
Односторонний предел - предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Существуют левый и правый пределы.
Число b называется правым пределом функции  в точке а, если для
в точке а, если для 
 такое, что для любого
такое, что для любого  и
и  , выполняется неравенство
, выполняется неравенство  .
.
Число b называется левым пределом функции f(x) в точке а, если для 
 такое, что для любого
такое, что для любого  и
и  , выполняется неравенство
, выполняется неравенство  .
.
8. Основные теоремы о пределах функций (о пределе суммы, произведения и частного функций), о пределах функций, связанных неравенствами, о пределе сложной функции.
1. Если каждое слагаемое алгебраической суммы (произведения/частного) функций имеет предел при х → а, то и алгебраическая сумма (произведение/частное) имеет предел при х → а, причем предел алгебраической суммы (произведения/частного) равен алгебраической сумме (произведению/частному) пределов.
2. Если в окрестности некоторой точки а значения функции f(x) не превосходят соответствующих значений функции g(x), то и предел функции f(x) в этой точке не превосходит предела функции g(x) в этой же точке.
3. Если функция y=f(x) имеет в точке aa конечный предел b и не принимает значения b в некоторой проколотой окрестности U(a) этой точки, а функция g(y) имеет в точке b конечный предел c, то сложная функция g(f(x)) имеет предел в точке a, равный c.
9. Первый замечательный предел, его следствия. Примеры.
Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю. (0/0) lim(x→0) sinx/x=1.
Следствия:
1. lim(x→0) x/sinx=1.
2. lim(x→0) sin(ax)/sin(bx)=ab.
3. lim(x→0) tanx/x=1.
4. lim(x→0) arcsinx/x=1.
5. lim(x→0) arctanx/x=1.
6. lim(x→0) 1−cosx/x2=1.
Примеры:
Задание 1. Найти предел 
 Решение. Воспользуемся заменой и первым замечательным пределом.
Решение. Воспользуемся заменой и первым замечательным пределом.


 Ответ.
Ответ. 
 Задание 2. Найти предел
Задание 2. Найти предел 
 Решение. Разложим тангенс на синус и косинус и воспользуемся свойствами пределов.
Решение. Разложим тангенс на синус и косинус и воспользуемся свойствами пределов.


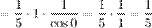
 Ответ.
Ответ. 
10. Второй замечательный предел, его следствия. Другие замечательные пределы. Примеры.
1. В случае второго замечательного предела имеем дело с неопределенностью вида единица в степени бесконечность (1∞) lim(x→∞) (1+(1/x))x=e или lim(x→0) (1+x)1/x=e.
Следствия:
1. lim(x→∞) (1+a/x)bx=eab.
2. lim(x→0) (ln(1+x))/x=1.
3. lim(x→0) (ex−1)/x=1.
4. lim(x→0) (ax−1)/xlna=1, a>0, a≠1.
5. lim(x→0) ((1+x)a−1)/ax=1.
Примеры:
Задание. Найти предел 
 Решение. Подставим
Решение. Подставим  , получим неопределенность и для решения предела воспользуемся вторым замечательным пределом.
, получим неопределенность и для решения предела воспользуемся вторым замечательным пределом.

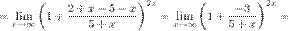

 Ответ.
Ответ. 
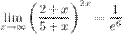 2. Другие замечательные пределы:
2. Другие замечательные пределы:
1.  2.
2.  3.
3. 
11. Бесконечно малые функции, определение и их свойства. Сравнение б.м. функций. О и о символика. Эквивалентные б.м. функции и их свойства. Эквивалентность некоторых функции в окрестности точки х=0.
1. Функция a(x) называется бесконечно малой функцией (б.м.ф.) при x→a (или в точке x=a), если  Свойства:
Свойства:
1. Сумма конечного числа б.м функций является функцией б.м.
2. Произведение б.м функции на ограниченную есть функция б.м.
3. Произведение двух б.м функций есть функция б.м.
4. Произведение б.м функции на константу является б.м функцией.
5. Частное от деления б.м функции на функцию, предел которой не равен нулю, есть функция б.м.
6. Функция  , обратная к б.м функции
, обратная к б.м функции  , есть функция бесконечно большая. Верно и обратное.
, есть функция бесконечно большая. Верно и обратное.
2. 1. Функции a(x) и b(x) называются б.м. одного порядка малости при x→a, если 
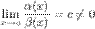 2. Если
2. Если  , то a(x) является б.м. более высокого порядка при x→a, чем b(x), а b(x) - б.м. более низкого порядка по сравнению с a(x): a(x)=a(b(x)) при x→a.
, то a(x) является б.м. более высокого порядка при x→a, чем b(x), а b(x) - б.м. более низкого порядка по сравнению с a(x): a(x)=a(b(x)) при x→a.
3. Если  , то a(x) - б.м. низшего порядка малости при x→a по сравнению с b(x).
, то a(x) - б.м. низшего порядка малости при x→a по сравнению с b(x).
4. Если  , то a(x) называется б.м. порядка k по сравнению с b(x) при x→a.
, то a(x) называется б.м. порядка k по сравнению с b(x) при x→a.
3.  4. Если
4. Если  , то б.м. функции a(x) и b(x) называются эквивалентными или равносильными б.м. одного порядка при x→a:
, то б.м. функции a(x) и b(x) называются эквивалентными или равносильными б.м. одного порядка при x→a:  при x→a.
при x→a.
Свойства:
1. 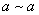 ,
, 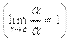 .
.
2. Если  и
и  , то
, то  ,
,  .
.
3. Если  и
и  , то
, то  .
.
4. Если  и
и  и
и  , то и
, то и  или
или  .
.
5. Для того чтобы функции f(x) и g(x) были эквивалентны при x  0, необходимо и достаточно, чтобы: f(x) = g(x) + o(g(x)), x
0, необходимо и достаточно, чтобы: f(x) = g(x) + o(g(x)), x  0.
0.
12. Функции действительного переменного, непрерывность в точке, их свойства. Непрерывность элементарных функций.
1. Функция  называется непрерывной в точке
называется непрерывной в точке  , если:
, если:
1. функция  определена в точке
определена в точке  и ее окрестности;
и ее окрестности;
2. существует конечный предел функции  в точке
в точке  ;
;
3. это предел равен значению функции в точке  , т.е.
, т.е. 
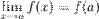 Свойства:
Свойства:
1. Если функции f (x) и g (x) непрерывны в точке х0, то в этой точке непрерывны.
2. Если функция u(x) непрерывна в точке х0, а функция f(u) непрерывна в соответствующей точке u0 = f(x0), то сложная функция f(u(x)) непрерывна в точке х0.
3. (ограниченность непрерывной функции). Если функция f(x) непрерывна в точке x0, то существует окрестность O(x0), в которой f(x)ограничена.
4. (устойчивость знака непрерывной функции). Если функция f(x) непрерывна в точке x0 и f(x0) ≠ 0, то существует окрестность точки x0, в которой f(x) ≠ 0, причем знак f(x) в этой окрестности совпадает со знаком f(x0).
2. Все элементарные функции являются непрерывными в любой точке свой области определения.
Функция называется элементарной, если она построена из конечного числа композиций и комбинаций (с использованием 4 действий - сложение, вычитание, умножение и деление) основных элементарных функции.
1. f(x) = C, (где С – постоянная) непрерывна на R, т.к.  при любом x.
при любом x.
2. f(x) = x, непрерывна на R, т.к.  при
при  .
.
3. f(x) =  , непрерывна на R как произведение непрерывных функций.
, непрерывна на R как произведение непрерывных функций.
4. f(x) = 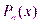 , непрерывна на R, т.к. многочлен
, непрерывна на R, т.к. многочлен  есть сумма непрерывных функций.
есть сумма непрерывных функций.
5. f(x) =  , где P и Q – многочлены степени n и m соответственно, непрерывна на R кроме тех x, при которых Q обращается в нуль, как частное непрерывных функций.
, где P и Q – многочлены степени n и m соответственно, непрерывна на R кроме тех x, при которых Q обращается в нуль, как частное непрерывных функций.
6. f(x) = sin(x), f(x) = cos(x)
7. f(x) = arcsin(x), f(x) = arccos(x), f(x) = arctg(x), f(x) = arcctg(x), непрерывны на своей области определения.
8.  , где r – рациональное. Представим r = m / n,
, где r – рациональное. Представим r = m / n,  . Тогда
. Тогда  . Функция
. Функция 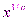 непрерывна и строго возрастает на R. По п. 2
непрерывна и строго возрастает на R. По п. 2  также непрерывна.
также непрерывна.
9. 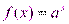 , a > 1, непрерывна на R. Пусть
, a > 1, непрерывна на R. Пусть  – произвольная точка множества R,
– произвольная точка множества R,  =
= 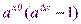 . Докажем, что
. Докажем, что  .
.
10. Логарифмическая функция непрерывна, что следует из непрерывности показательной функции по теореме об обратной функции.
13. Точки разрыва функции, их классификация.
Точка  , в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:
, в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:
1. функция  определена в точке и ее окрестности;
определена в точке и ее окрестности;
2. существует конечный предел функции  в точке
в точке  ;
;
3. это предел равен значению функции в точке  , т.е.
, т.е. 
 называется точкой разрыва функции.
называется точкой разрыва функции.
Классификация:
1. Точка разрыва первого рода: если в точке  существуют конечные пределы
существуют конечные пределы  и
и  , такие, что
, такие, что  .
.
2. Точка разрыва второго рода: если хотя бы один из пределов  или
или  не существует или равен бесконечности.
не существует или равен бесконечности.
3. Точка устранимого разрыва: если существуют левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением функции  в точке
в точке  :
:  или функция
или функция  не определена в точке
не определена в точке  .
.
14. Непрерывность функции на интервале, на отрезке. Формулировка свойств функций, непрерывных на отрезке.
1. Функция  называется непрерывной на интервале
называется непрерывной на интервале  , если она непрерывна в каждой точке этого интервала.
, если она непрерывна в каждой точке этого интервала.
Функция  называется непрерывной на отрезке
называется непрерывной на отрезке 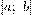 , если она непрерывна на интервале
, если она непрерывна на интервале  , непрерывна справа в точке а и непрерывна слева в точке b.
, непрерывна справа в точке а и непрерывна слева в точке b.
2. 1. (Об ограниченности непрерывной на отрезке функции). Если функция  непрерывна на отрезке
непрерывна на отрезке 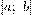 , то она и ограничена на этом отрезке, то есть существует такое число
, то она и ограничена на этом отрезке, то есть существует такое число  , что для любого
, что для любого 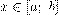 выполняется неравенство
выполняется неравенство  .
.
2. (Теорема Вейерштрасса). Если функция  непрерывна на отрезке
непрерывна на отрезке 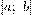 , то она достигает на этом отрезке своего наибольшего M и наименьшего m значений.
, то она достигает на этом отрезке своего наибольшего M и наименьшего m значений.
3. (О существовании нуля на отрезке непрерывности). Если функция  непрерывна на отрезке
непрерывна на отрезке 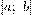 и на концах отрезка принимает ненулевые значения разных знаков, то на интервале
и на концах отрезка принимает ненулевые значения разных знаков, то на интервале  найдется по крайней мере одна точка c, в которой
найдется по крайней мере одна точка c, в которой 
 4. (Теорема Больцано-Коши). Если функция
4. (Теорема Больцано-Коши). Если функция  непрерывна на отрезке
непрерывна на отрезке 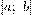 , то она принимает на интервале
, то она принимает на интервале  все промежуточные значения между
все промежуточные значения между 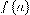 и
и  .
.
5. (О существовании непрерывной обратной функции). Пусть функция  определена, строго монотонна и непрерывна на отрезке
определена, строго монотонна и непрерывна на отрезке 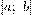 . Тогда на отрезке
. Тогда на отрезке  , где
, где  , существует обратная функция
, существует обратная функция  также строго монотонная и непрерывная на отрезке
также строго монотонная и непрерывная на отрезке  .
.
Раздел II. Дифференциальное исчисление функции одной переменной.
15. Производная функции действительного переменного, её геометрический и механический смысл. Касательная и нормаль к кривой.
1. Механический: пусть задан путь  движения материальной точки. Скорость данной материальной точки в момент времени
движения материальной точки. Скорость данной материальной точки в момент времени  есть производная от пути
есть производная от пути  по времени
по времени  :
: 

 Геометрический: Производная функции
Геометрический: Производная функции 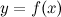 , вычисленная при заданном значении
, вычисленная при заданном значении  , равна тангенсу угла, образованного положительным направлением оси
, равна тангенсу угла, образованного положительным направлением оси  и положительным направлением касательной, проведенной к графику этой функции в точке с абсциссой
и положительным направлением касательной, проведенной к графику этой функции в точке с абсциссой  :
: 


 Геометрически производная представляет собой угловой коэффициент касательной к графику функции
Геометрически производная представляет собой угловой коэффициент касательной к графику функции 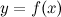 в точке
в точке  .
.
2. Касательная прямая - прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.
Прямая, проходящая через точку касания, перпендикулярно касательной, называется нормалью к кривой.
Если кривая определена уравнением  , то уравнение касательной к ней в точке
, то уравнение касательной к ней в точке  имеет вид:
имеет вид:  , а уравнение нормали:
, а уравнение нормали: 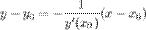
16. Односторонние производные. Необходимые условия существования производной.
1. Если существует  =
=  =f+’(x0), то его называют правосторонней производной функции f(x) в т. x0. Аналогично
=f+’(x0), то его называют правосторонней производной функции f(x) в т. x0. Аналогично  =
=  =f-’(x0) называют левосторонней производной.
=f-’(x0) называют левосторонней производной.
2. 1. Если функции имеют угловые точки (функции, содержащие знак модуля), то в этих точках производная не существует.
2. Если  = ∞, то такую производную называют бесконечной производной.
= ∞, то такую производную называют бесконечной производной.
3. Если функция в точке x0 имеет производную, то она дифференцируема в точке x0.
4. Теорема (необходимое условие существования производной функции в точке). Если функция y = f(x) имеет производную в точке x0, то функция f(x) в этой точке непрерывна.
17. Таблица производных. Общие правила дифференцирования.
1. 
 2.
2.  - производная сложной функции.
- производная сложной функции.
 - производная на константу.
- производная на константу.
18. Дифференцирование сложной функции, обратной функции.
1. (о производной сложной функции). Если функция u(x) дифференцируема в точке x0, а функция y = f(u) дифференцируема в соответствующей точке u0 = u(x0), тогда сложная функция F(x) = f(u(x)) дифференцируема в точке x0, причем: F '(x 0) = f '(u 0) · u '(x 0).
2. (о производной обратной функции). Пусть функция y = f (x) взаимно однозначна в интервале (a, b), содержащем точку x 0. Пусть в точке x 0 она имеет конечную и отличную от нуля производную f '(x 0). Тогда обратная функция x = g (y) также имеет производную в соответствующей точке y 0 = f (x 0), причем: g '(y 0) = 1/f '(х0)
19. Логарифмическое дифференцирование. Дифференцирование неявных функции.
1. Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него.
Суть такого дифференцирования заключается в следующем: вначале находится логарифм заданной функции, а уже затем вычисляется от него производная. Пусть задана некоторая функция 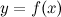 . Прологарифмируем левую и правую части данного выражения:
. Прологарифмируем левую и правую части данного выражения: 
 Далее продифференцируем полученное равенство при условии, что
Далее продифференцируем полученное равенство при условии, что  является функцией от
является функцией от  , то есть найдемпроизводную сложной функции:
, то есть найдемпроизводную сложной функции: 
 А тогда, выражая искомую производную
А тогда, выражая искомую производную  , в результате имеем:
, в результате имеем: 


 2.
2. 
20. Дифференциал функции, его геометрический смысл, свойства, инвариантная форма записи. Формула для приближенных вычислений.
1. Дифференциал функции y = f(x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x; y), при изменении x (аргумента) на величину 

 Свойства:
Свойства:
Дифференциал обладает свойствами, аналогичными свойствам производной:
1. 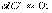 (С – постоянная величина) 2.
(С – постоянная величина) 2. 
3.  4.
4.  5.
5. 
 Дифференциал функции в точке x и обозначают
Дифференциал функции в точке x и обозначают  или
или 
 2.
2. 
21. Производные высших порядков. n-ая производная для некоторых функции.


22. Функции, заданные параметрически, их дифференцирование.
1. Формулы  задают параметрическое представление функции одной переменной.
задают параметрическое представление функции одной переменной.
2. Пусть функция  задана в параметрической форме, то есть в виде:
задана в параметрической форме, то есть в виде: 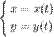 , где функции
, где функции  и
и  определены и непрерывны на некотором интервале изменения параметра
определены и непрерывны на некотором интервале изменения параметра  . Найдем дифференциалы от правых и левых частей каждого из равенств:
. Найдем дифференциалы от правых и левых частей каждого из равенств:  Далее, разделив второе уравнение на первое, и с учетом того, что
Далее, разделив второе уравнение на первое, и с учетом того, что  , получим выражение для первой производной функции, заданной параметрически:
, получим выражение для первой производной функции, заданной параметрически:  Для нахождения второй производной
Для нахождения второй производной  выполним следующие преобразования:
выполним следующие преобразования: 
23. Убывание и возрастание функции в точке. Теоремы Ферма, Ролля, их геометрический смысл.
1. 1. Будем говорить, что функция y=f(x) возрастает в точке с, если найдется такая окрестность точки с, в пределах которой  и
и 
 2. Будем говорить, что функция y=f(x) убывает в точке с, если найдется такая -окрестность точки с, в пределах которой
2. Будем говорить, что функция y=f(x) убывает в точке с, если найдется такая -окрестность точки с, в пределах которой  и
и 
 3. Будем говорить, что функция y=f(x) имеет в точке с локальный максимум [локальный минимум], если найдется такая окрестность точки с, в пределах которой значение f(c) является наибольшим [наименьшим] среди всех значений f(x) этой функции.
3. Будем говорить, что функция y=f(x) имеет в точке с локальный максимум [локальный минимум], если найдется такая окрестность точки с, в пределах которой значение f(c) является наибольшим [наименьшим] среди всех значений f(x) этой функции.
4. Будем говорить, что функция y=f(x) имеет в точке с локальный экстремум, если эта функция имеет, в указанной точке либо локальный максимум, либо локальный минимум.
2. 1. Теорема Ферма. (О равенстве нулю производной): Пусть функция 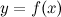 удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
1) она дифференцируема на интервале 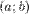 ;
;
2) достигает наибольшего или наименьшего значения в точке  .
.
Тогда производная в этой точке равна нулю, то есть  .
.
Следствие. (Геометрический смысл теоремы Ферма): В точке наибольшего и наименьшего значения, достигаемого внутри промежутка, касательная к графику функции параллельна оси абсцисс.
2. Теорема Ролля. (О нуле производной функции, принимающей на концах отрезка равные значения): Пусть функция 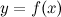
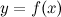 1) непрерывна на отрезке
1) непрерывна на отрезке  ;
;
2) дифференцируема на интервале 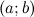 ;
;
3) на концах отрезка  принимает равные значения
принимает равные значения  .
.
Тогда на интервале  найдется, по крайней мере, одна точка
найдется, по крайней мере, одна точка  , в которой
, в которой 
 Следствие. (Геометрический смысл теоремы Ролля)
Следствие. (Геометрический смысл теоремы Ролля)
Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс.
24. Теорема Лагранжа, её геометрический смысл. Следствия теоремы Лагранжа.
1. Теорема Лагранжа. (О конечных приращениях): Пусть функция 
 1) непрерывна на отрезке
1) непрерывна на отрезке  ;
;
2) дифференцируема на интервале  .
.
Тогда на интервале 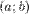 найдется по крайней мере одна точка
найдется по крайней мере одна точка  , такая, что
, такая, что 
 Теорема Ролля есть частный случай теоремы Лагранжа, когда
Теорема Ролля есть частный случай теоремы Лагранжа, когда  .
.
2. Следствие. (Геометрический смысл теоремы Лагранжа): На кривой  между точками
между точками  и
и  найдется точка
найдется точка  , такая, что через эту точку можно провести касательную, параллельную хорде АВ.
, такая, что через эту точку можно провести касательную, параллельную хорде АВ.
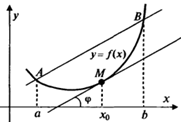
 Доказанная формула называется формулой Лагранжа или формулой конечных приращений. Она может быть переписана в виде:
Доказанная формула называется формулой Лагранжа или формулой конечных приращений. Она может быть переписана в виде: 
 1. В частном случае, когда f(b)=f(a), из теоремы Лагранжа вытекает, что существует точка c принадлежит (a,b), в которой производная функции f(x) равна нулю: f’(c)=0. Это означает, что теорема Лагранжа является обобщением теоремы Ролля.
1. В частном случае, когда f(b)=f(a), из теоремы Лагранжа вытекает, что существует точка c принадлежит (a,b), в которой производная функции f(x) равна нулю: f’(c)=0. Это означает, что теорема Лагранжа является обобщением теоремы Ролля.
2. Если f’(x)=0 во всех точках некоторого промежутка [a,b], то f(x)=const в этом промежутке.
Действительно, пусть x1 и x2 – произвольные точки промежутка [a,b] и x1<x2. Применяя теорему Лагранжа к промежутку [x1,x2], получим 
 Однако f’(x)=0 во всех точках промежутка [a,b]. Тогда
Однако f’(x)=0 во всех точках промежутка [a,b]. Тогда 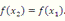
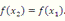 Учитывая произвольность точек x1 и x2, получаем требуемое утверждение.
Учитывая произвольность точек x1 и x2, получаем требуемое утверждение.
25. Правила Лопиталя-Бернулли.
1. Рассмотрим функции  , которые бесконечно малЫв некоторой точке
, которые бесконечно малЫв некоторой точке  . Если существует предел их отношений
. Если существует предел их отношений  , то в целях устранения неопределённости
, то в целях устранения неопределённости  можно взять две производные – от числителя и от знаменателя. При этом:
можно взять две производные – от числителя и от знаменателя. При этом:  , то есть при дифференцировании числителя и знаменателя значение предела не меняется.
, то есть при дифференцировании числителя и знаменателя значение предела не меняется.
2. Если существует предел отношения бесконечно больших в точке  функций:
функций:  , то в целях устранения неопределённости
, то в целях устранения неопределённости  можно взять две производные – ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. При этом:
можно взять две производные – ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. При этом:  , то есть при дифференцировании числителя и знаменателя значение предела не меняется.
, то есть при дифференцировании числителя и знаменателя значение предела не меняется.
26. Формула Тейлора с остаточным членом в форме Пеано и Лагранжа. Формула Маклорена.
1. 1. 
 Последнее слагаемое
Последнее слагаемое  называется остаточным членом в форме Пеано.
называется остаточным членом в форме Пеано.
2. Rn(x) = 
 2.
2.  Полученное выражение называется формулой Маклорена для многочлена P(x) степени n.
Полученное выражение называется формулой Маклорена для многочлена P(x) степени n.
27. Разложение по формуле Маклорена функций ex, sin x, cos x, ln (1+x), (1+х) n.

28. Необходимые и достаточные условия монотонности функции. Экстремум функции, его необходимое условие, достаточные условия экстремума.
1. Необходимое: Если дифференцируемая в интервале (а, b) функция у = f (х) возрастает (убывает) на этом интервале, то ее производная в каждой точке (а, b) 
 .
.
Достаточные: Если непрерывная на отрезке [ а, b ] функция у = f (х) в каждой точке интервала (а, b) имеет положительную (отрицательную) производную, то эта функция возрастает (убывает) на отрезке [ а, b ].
2. 1. Точка  называется точкой локального максимума функции
называется точкой локального максимума функции  , если существует такая окрестность этой точки, что для всех
, если существует такая окрестность этой точки, что для всех  из этой окрестности вы
из этой окрестности вы