Краткая теория
· Второй закон Ньютона (уравнение движения материальной точки):
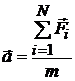 , или
, или 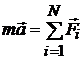 ,
,
где 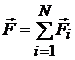 – векторная сумма сил, действующих на материальную точку (равнодействующая всех сил); т – масса;
– векторная сумма сил, действующих на материальную точку (равнодействующая всех сил); т – масса; 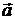 – ускорение; N – число сил, действующих на точку.
– ускорение; N – число сил, действующих на точку.
В проекциях на координатные оси:
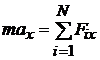 ;
; 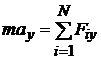 ,
, 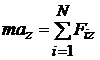 ,
,
или
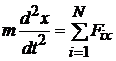 ;
; 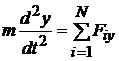 ,
, 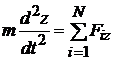 ,
,
где под знаком суммы стоят проекции сил 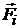 , на соответствующие оси.
, на соответствующие оси.
· Импульс тела массой 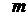 , движущегося со скоростью
, движущегося со скоростью  :
:
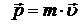 .
.
При скоростях 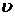 , сравнимых со скоростью света в вакууме (
, сравнимых со скоростью света в вакууме (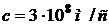 ), необходимо использовать формулы для релятивистского импульса:
), необходимо использовать формулы для релятивистского импульса:
 или
или 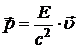 ,
,
где Е – полная энергия частицы, равная сумме энергии покоя 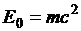 и кинетической энергии:
и кинетической энергии: 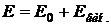 . Полная энергия частицы и её импульс связаны следующей релятивистской формулой:
. Полная энергия частицы и её импульс связаны следующей релятивистской формулой:
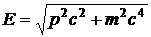 .
.
· Импульс силы:
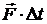 ,
,
где  – промежуток времени, в течение которого действовала сила
– промежуток времени, в течение которого действовала сила 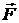 .
.
· Второй закон Ньютона в импульсной форме:
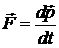 , или
, или 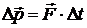
где 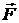 – равнодействующая,
– равнодействующая, 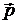 – импульс тела,
– импульс тела, 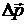 – изменение импульса за промежуток времени
– изменение импульса за промежуток времени  действия силы.
действия силы.
· Третий закон Ньютона. Тела действуют друг на друга с силами, равными по величине и направленными противоположно вдоль одной прямой:
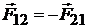 ,
,
где 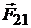 – сила, с которой первое тело действует на второе, а
– сила, с которой первое тело действует на второе, а 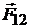 – второе на первое.
– второе на первое.
· Центр масс. Радиус-вектор 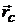 центра масс равен
центра масс равен
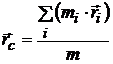 ,
,
где 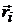 – радиус-вектор точечной массы
– радиус-вектор точечной массы  ,
,  – масса всей системы (тела).
– масса всей системы (тела).
 Координаты центра масс системы материальных точек:
Координаты центра масс системы материальных точек:
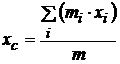 ,
, 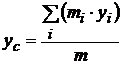 ,
, 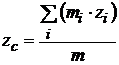 ,
,
где xi, yi;, zi – координаты i -й материальной точки.
 Закон всемирного тяготения
Закон всемирного тяготения
 ,
,
где γ – гравитационная постоянная; m 1 и m 2 – массы взаимодействующих тел, рассматриваемые как материальные точки; r – расстояние между ними.
 Сила притяжения тела массой m к Земле (или другому небесному телу) массой M радиусом R на высоте h над поверхностью (сила тяжести):
Сила притяжения тела массой m к Земле (или другому небесному телу) массой M радиусом R на высоте h над поверхностью (сила тяжести):
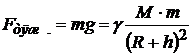 .
.
Здесь γ – гравитационная постоянная, g – ускорение свободного падения на высоте h:  .
.
 Сила тяжести на поверхности Земли:
Сила тяжести на поверхности Земли:
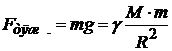 ,
,
где 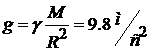 – ускорение свободного падения
– ускорение свободного падения
 Вес тела, движущегося с ускорением
Вес тела, движущегося с ускорением 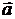 :
:
 ,
,
где m – масса тела. Если ускорение тела направлено вертикально вверх, то вес 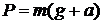 ; а если вертикально вниз, то
; а если вертикально вниз, то 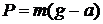 .
.
 Сила трения скольжения:
Сила трения скольжения:
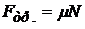 ,
,
где 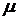 – коэффициент трения скольжения; N – сила нормального давления.
– коэффициент трения скольжения; N – сила нормального давления.
 Сила упругости (закон Гука):
Сила упругости (закон Гука):
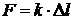 ,
,
где k – коэффициент упругости (коэффициент жесткости); 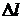 – абсолютная деформация.
– абсолютная деформация.
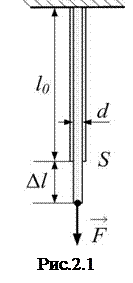
 Относительная продольная деформация
Относительная продольная деформация 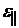 (или просто
(или просто  ) – это изменение длины тела
) – это изменение длины тела 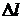 по отношению к первоначальной длине
по отношению к первоначальной длине 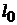 (рис.2.1):
(рис.2.1):
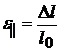 .
.
 Механическое напряжение (нормальное механическое напряжение) σ – это сила, приходящаяся на единицу площади сечения тела (сила приложена перпендикулярно сечению
Механическое напряжение (нормальное механическое напряжение) σ – это сила, приходящаяся на единицу площади сечения тела (сила приложена перпендикулярно сечению 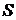 ):
):
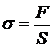 .
.
 Закон Гука в локальной (дифференциальной) форме:
Закон Гука в локальной (дифференциальной) форме:
 ,
,
где 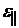 – относительная деформация; σ – механическое напряжение;
– относительная деформация; σ – механическое напряжение; 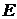 – модуль Юнга материала.
– модуль Юнга материала.
 Давление – это сила F, приходящаяся на единицу площади S:
Давление – это сила F, приходящаяся на единицу площади S:
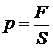 .
.
 Плотность тела
Плотность тела
 ,
,
где m – масса тела; V – его объём.
 Гидростатическое давление:
Гидростатическое давление:
 ,
,
где ρ – плотность; g – ускорение свободного падения; h – глубина под свободной поверхностью жидкости.
 Выталкивающая (Архимедова) сила:
Выталкивающая (Архимедова) сила:
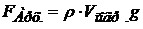 ,
,
где ρ – плотность жидкости (газа); Vпогр. – объём погружённой части тела.
 Момент силы:
Момент силы:
 ,
,
где l – плечо силы (кратчайшее расстояние от линии силы до оси вращения).
 Условие равновесия твёрдого тела
Условие равновесия твёрдого тела
равнодействующая всех сил равна нулю:
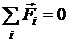 ;
;
сумма моментов всех сил относительно любой оси тоже равна нулю:
 .
.
Примеры решения задач
Пример 2.1. На автомобиль массой 1 тонна во время движения действует сила трения, равная 0.1 силы тяжести. Чему должна быть равна сила тяги автомобиля, чтобы автомобиль двигался: а) равномерно; б) равноускоренно с ускорением 2 м/с2?
| Дано: m =1 т=1000 кг F тр.=0.1. mg а) а =0 б) а =2 м/с2 |
| Найти: F тяги=? |
Решение
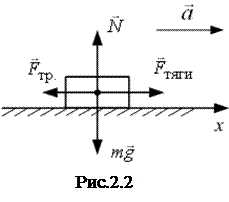
На рисунке 2.2 показаны силы, действующие на автомобиль: сила тяжести 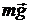 , сила реакции опоры
, сила реакции опоры 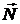 , сила тяги
, сила тяги  и сила трения
и сила трения 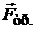 . Запишем второй закон Ньютона в векторной форме:
. Запишем второй закон Ньютона в векторной форме:
 .
.
В проекциях на ось OX:
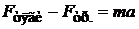
а) В случае а =0 получим:
F тяги= F тр.= 0.1. mg;
F тяги=0.1.1000 кг.10 м/с2=1000 Н=1 кН.
б) В случае а =2 м/с2 получим:
F тяги= F тр.+ ma .=0.1. mg .+ ma .= m .(0.1. g .+ a);
F тяги=1000 кг.(0.1.10 м/с2 +2 м/с2)=3000 Н=3 кН.
Ответ: а) F тяги=1 кН; б) F тяги=3 кН.
Законы сохранения
Краткая теория
 Закон сохранения импульса: в замкнутой системе полный импульс сохраняется.
Закон сохранения импульса: в замкнутой системе полный импульс сохраняется.
Закон сохранения импульса справедлив и в случае, если внешние силы действуют на систему, но компенсируют друг друга:
если 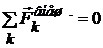 , то
, то 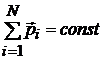 (или
(или 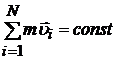 ).
).
где N — число материальных точек (или тел), входящих в систему.
Даже если равнодействующая внешних сил не равна нулю, но равна нулю её проекция на какую-либо ось, то проекция полного импульса системы на ту же ось сохраняется:
если 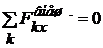 , то
, то  .
.
 Работа, совершаемая постоянной силой:
Работа, совершаемая постоянной силой:
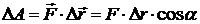 ,
,
где 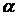 – угол между направлениями векторов силы
– угол между направлениями векторов силы 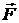 и перемещения
и перемещения 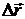 .
.
 Работа, совершаемая переменной силой:
Работа, совершаемая переменной силой:
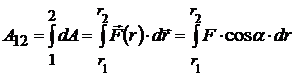 ,
,
где интегрирование ведется вдоль траектории от точки 1 с радиус-вектором  до точки 2 с радиус-вектором
до точки 2 с радиус-вектором 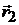 .
.
 Средняя мощность – работа за единицу времени:
Средняя мощность – работа за единицу времени:
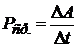 ,
,
где Δ А – работа, совершённая за время Δ t.
 Мгновенная мощность – быстрота совершения работы:
Мгновенная мощность – быстрота совершения работы:
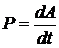 , или
, или 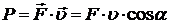 .
.
 Коэффициент полезного действия (КПД):
Коэффициент полезного действия (КПД):
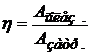 .
.
 Кинетическая энергия материальной точки (или тела), движущейся поступательно:
Кинетическая энергия материальной точки (или тела), движущейся поступательно:
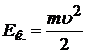 , или
, или 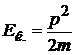 .
.
 Потенциальная энергия тела в однородном поле силы тяжести:
Потенциальная энергия тела в однородном поле силы тяжести:
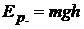 ,
,
где h – высота тела над уровнем, принятым за начало отсчета. Эта формула справедлива при условии 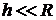 , где R – радиус Земли. Если это условие не соблюдается, то
, где R – радиус Земли. Если это условие не соблюдается, то
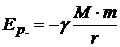 .
.
Здесь 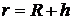 – расстояние до центра планеты.
– расстояние до центра планеты.
 Потенциальная энергия упруго деформированного тела:
Потенциальная энергия упруго деформированного тела:
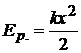 ,
,
где k – жёсткость (коэффициент упругости), x =Δ l – абсолютная деформация (удлинение) тела.
 Закон сохранения энергии. Полная энергия замкнутой системы сохраняется:
Закон сохранения энергии. Полная энергия замкнутой системы сохраняется:
если 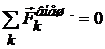 , то
, то  , или
, или 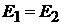 ,
,
где Е 1 – начальная полная энергия системы (сумма всех видов энергии: механической, внутренней, электромагнитной и т.д.); Е 2 – конечная полная энергия системы.
 Закон сохранения механической энергии. Полная механическая энергия замкнутой системы, в которой действуют только консервативные силы, остаётся постоянной:
Закон сохранения механической энергии. Полная механическая энергия замкнутой системы, в которой действуют только консервативные силы, остаётся постоянной:
если 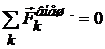 , то
, то 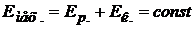 , или
, или  .
.
При наличии диссипативных сил (силы трения, вязкости, силы неупругой деформации) закон сохранения (изменения) механической энергии при переходе системы из состояния 1 в состояние 2:
 ,
,
Если есть любые внешние силы:
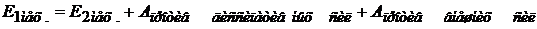 .
.
Примеры решения задач
Дано:
m 1=9.10-3 кг
m 2=16.10-3 кг
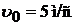 α1=α2=α
α1=α2=α
|
| Найти: υ 1=? υ 2=? β =? |
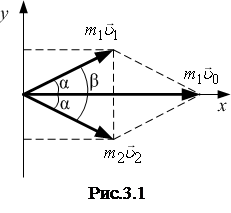
Пример 3.1. Шарик массой m 1=9 г, движущийся со скоростью 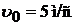 , сталкивается с покоящимся шариком массой m 2=16 г. После абсолютно упругого удара шарики разлетаются таким образом, что направления их скоростей составляют одинаковые углы с направлением скорости
, сталкивается с покоящимся шариком массой m 2=16 г. После абсолютно упругого удара шарики разлетаются таким образом, что направления их скоростей составляют одинаковые углы с направлением скорости 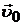 . Определить скорости
. Определить скорости  и
и  шариков после удара и угол β между векторами скоростей
шариков после удара и угол β между векторами скоростей  и
и  .
.
Решение
По закону сохранения импульса (рис.3.1):
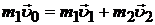 .
.
В проекциях на координатные оси:
 OX:
OX: 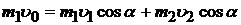 (1)
(1)
OY: 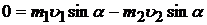 (2)
(2)
Из (2) следует:
 , (3)
, (3)
тогда (1) можно записать:
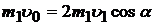 (4)
(4)
Удар абсолютно упругий, поэтому сохраняется полная механическая энергия:
 (5)
(5)
Решая уравнение (5) совместно с (3), найдём скорости υ 1 и υ 2: 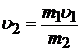 ;
;
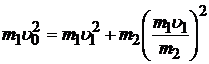
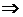

 ;
;
 .
.
Расчёты:
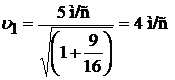 ;
;  .
.
Из (4) выразим cosα:
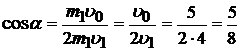 ;
; 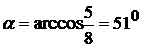 .
.
Тогда β =2α=1020.
Ответ: υ 1=4 м/с; υ 2=2.25 м/с; β =1020.