ДИДАКТИЧЕСКИЕ МАТЕРИАЛЫ ПО ГЕОМЕТРИИ

Зив Б. Г., Мейлер В. М.

Дидактические материалы по геометрии для 8 класса.— М.: Просвещение, 2000.

Охраняется Законом РФ «Об авторском праве и смежных правах». Воспроизведение всей книги или ее части на любых видах носителей запрещается без письменного разрешения издательства.

Переводное издание учебника выпущено в свет по Лицензионному договору 3/7 от 01.04.2002 г. Экземпляры переводного издания подлежат распространению исключительно на территории Республики Татарстан, а также среди татарской диаспоры на территориях других субъектов Россий­ской Федерации.

Зив Б. Г., Мейлер В. М..

3-47 Геометриядән дидактик материаллар: Татар урта гомуми белем бирү мәкт. 8 нче с-фы өчен /Русчадан Э. Р. Гыйльма- нова тәрҗ.— Казан: Мәгариф, 2003.— 143 б.: рәс. б-н.

ISBN 5-7761-1028-9

Әлеге ярдәмлектә мөстәкьГЙльЪәм контроль эш күнегүләре, шулай ук 8 нче сыйныф геометрия курсы, буенча математик диктантлар бирелә. Бу китап Л. С. Атанасян редакциясендәге «Геометрия, 7—9» дәреслегенә кулланма буларак тәкъдим ителә.

БЗ—10(69)-52-2003/2004

©Издательство «Просвещение», 1996 © Художественное оформление.

Издательство «Просвещение», 2000 Все права защищены © Татарчага тәрҗемә, «Мәгариф» нәшрияты, 2003

КЕРЕШ

Ярдәмлектә 39 мөстәкыйль эш, 7 контроль эш, 5 математик диктант һәм аеруча катлаулы мәсьәләләр бирелгән.

Мөстәкыйль эшләр тиңдәшле номеры һәм М хәрефе белән билгеләнгән. Мәсәлән, М—2 — икенче мөстәкыйль эш. Тәкъдим ителгән мөстәкыйль эшләрнең максаты — укучыларның индивидуаль үзенчәлекләрен һәм хәзерлек дәрәҗәләрен исәпкә алып, ал арның эшчәнлекләрен мәсьәләләр чишүгә юнәлтүдә ярдәм итү. Моннан тыш мөстәкыйль эшләрне көндәлек тикшерү өчен файдаланырга мөмкин.

Мөстәкыйль эшләр сигез вариантта бирелгән.

һәр эшнең беренче һәм икенче вариант мәсьәләләрен чишү өчен, укучылар минималь программа таләпләре дәрәҗәсендәге белемне кулланырга тиеш.

Өченче һәм дүртенче вариантлар уртача катлаулылыктагы мәсьәләләрдән тора. Бу мәсьәләләрне чишү өчен, стандарт ситуа­цияләрдәге төшенчәләрне танып белергә, стандарт яки аннан беразга гына аерылган шартларда белемнәрне куллана белергә кирәк. Өченче һәм дүртенче вариант мәсьәләләре катлаулылыгы буенча дәреслектәге күпчелек мәсьәләләргә охшаш.

Бишенче һәм алтынчы вариантлар яхшырак әзерлекле уку­чылар өчен бирелә. Бу варианттагы мәсьәләләрне чишү катлаулы ситуацияләрдә белемнәрне куллана белү, җитәрлек югары дәрә­җәдә хисаплау күнекмәләре һәм бердәй рәвеш үзгәртү күнекмә­ләре булдыруны таләп итә.

Бу мәсьәләләр катлаулылыгы буенча дәреслекнең авыррак типтагы һәм өстәмә мәсьәләләренә якынча туры килә.

Җиденче һәм сигезенче вариант мәсьәләләрен чишкәндә белемне иҗади куллана белү таләп ителә. Монда стандарт булма­ган катлаулы геометрик ситуацияләрне анализларга, мөстәкыйль рәвештә яңа фактлар ачарга, алар арасындагы нисбәтләрне ачыкларга туры килә. Катлаулылыклары буенча бу мәсьәләләр дәреслекнең «аеруча катлаулы мәсьәләләр» бүлегенә туры килә.

Җиденче һәм сигезенче вариант мәсьәләләрен укучыларга, сыйныфның барлык укучылары белән төп эшләрен башкарганнан соң, калган вакытта бирергә, мәҗбүри булмаган өй эше өчен, шулай ук факультатив яки математик түгәрәк утырышларында файдаланырга мөмкин.

Ярдәмлектә * тамгасы белән билгеләнгән ике мөстәкыйль эш бирелгән. Бу эшләрнең беренче һәм икенче вариантлары катлау­лылык дәрәҗәсе минималь программа таләпләренә караганда бераз авыррак. Аларны яхшырак әзерлекле сыйныфларда үткәрергә тәкъдим ителә.

Ярдәмлектә мөстәкыйль эшләр бик күп. Укытучы укучылар һәр эштәге барлык биремнәрне дә эшләп бетерергә тиеш дигән

максат куярга тиеш түгел. Ярдәмлектәге эшләр җыелмасы укытучыга һәр дәрестә дәреснең максатына, вакытына, укучылар­ның хәзерлек дәрәҗәсенә карап кирәкле биремнәрне сайлап алыр­га мөмкинлек бирә.

Ярдәмлектәге эшләр вариантлап төзелгән.

Биремнәрнең сигез вариантта булуы, бер китапны һәр укучыга аерым бирерлек итеп, сигез кечкенә китапка бүләргә мөмкинлек бирә.

Контроль эшләр ярдәмлектә тиңдәшле номеры һәм К хәрефе белән билгеләнгән. Алар дәреслекнең һәр биш бүлеге һәм бөтен 8 нче сыйныф геометрия курсы буенча белемнәрне йомгаклап тикшерү эшләре үткәрү өчен бирелгән.

Контроль эшләр дүрт вариантта төзелгән. Барлык вариантлар­ның эшләре якынча бер үк катлаулылыкта. Ьәр вариантта⁰ тамгасы белән билгеләнгән ике бирем бар. Бу — минималь программа таләпләре дәрәҗәсендәге мәсьәләләр. Алар эшнең мәҗбүри өлешен тәшкил итәләр.

Киләсе өч бирем укучыларның математик белем үсешен тик­шерә. Шул ук вакытта соңгы бирем белемнәрне иҗади куллану, стандарт булмаган геометрик конфигурацияләрне анализлау, җитәрлек дәрәҗәдә катлаулы дедуктив фикер йөртүне таләп итә. Бу бирем * тамгасы белән билгеләнгән.

Ьәр эшне үткәргәндә укытучы, укучыларның хәзерлек дәрә­җәсенә һәм эшкә бирелгән вакытка бәйле рәвештә,⁰ тамгасы белән билгеләнмәгән мәсьәләләрнең кайсын бу эшкә кертүне үзе хәл итә. Мәсәлән, К—1 контроль эше өчен (45 минутка каралган) биремнәрне түбәндәгечә төзеп була:

— 1°, 2°, За яисә 1°, 2°, 36 биремнәре хәзерлек дәрәҗәсе йомшак сыйныфлар өчен;

— 1,2,36, яисә 1°, 2°, 36, 4*, яисә 1°, 2°, За, 36, 4* биремнәре әзерлек дәрәҗәсе көчле сыйныфлар өчен.

Бу вакытта «3» ле билгесен алу өчен, 1° һәм 2° биремнәрен дөрес эшләү җитә.⁰ тамгасы белән билгеләнмәгән мәсьәләләрне чишү исә, «4» һәм «5» билгеләрен алу өчен яки ике — төп һәм өстәмә билге алу өчен, кирәкле шарт булып тора.

Контроль эшләрне банткача да кулланырга мөмкин.

Математик диктантлар укучыларның теоретик белемнәрен системага салу максаты белән бирелә һәм контроль эш алдыннан үткәрелергә мөмкин. Диктант үткәргәндә укытучы сорау яки мәсьәлә тәкъдим итә, ә укучы берничә минут эчендә аларга җавап бирергә тиеш. Җавап өчен кирәкле вакытны, сорауның катлау­лыгына һәм сыйныфның хәзерлегенә карап, укытучы үзе билгели. Мондый эш өчен якынча 35 минут вакыт бирелергә мөмкин, калган вакытта укытучы сыйныф белән укучыларның җавапла­рын тикшерә, хаталарны күрсәтә.

Ярдәмлек ахырында барлык мөстәкыйль эшләргә, контроль эшләргә җаваплар, шулай ук катлаулырак биремнәргә күрсәтмә­ләр һәм аларның чишелешләре бирелгән. Күп мәсьәләләрнең ярдәмлектә тәкъдим ителмәгән башка чишелешләре дә бар.

Дәреслек пунктлары буенча мөстәкыйль һәм
контроль эшләрнең бүленеше

Мөстә­кыйль эш	Тема	Дәреслек пункты
М—1	Күппочмак, дүртпочмак	39—41
М—2	Параллелограмм һәм аның үзлекләре
М—3	Параллелограммның билгеләре
М—4	Трапеция
М—5	Параллелограмм һәм трапеция төзүгә мәсьәләләр	42—44
М—6	Турыпочмаклык
М—7	Ромб һәм квадрат
М—8	Турыпочмаклык, ромб, квадрат төзүгә мәсьәләләр	45, 46
М—9	Күппочмаклар, квадрат һәм турыпочмаклык мәйданнарының
	үзлекләре	48, 50
М—10	Параллелограмм мәйданы
М—11	Өчпочмак мәйданы
М—12	Трапеция мәйданы
М—13	Пифагор теоремасы	54, 55
М—14	Күппочмаклар мәйданы	48—55
М—15	Пропорциональ кисемтәләр
М—16	Охшаш өчпочмаклар билгеләмәсе
	Охшаш өчпочмаклар мәйданнарының чагыштырмасы	57, 58
М—17	Өчпочмаклар охшашлыгының беренче билгесе
М—18	Өчпочмаклар охшашлыгының икенче һәм өченче билгеләре	60,61
М—19	Өчпочмакның урта сызыгы. Өчпочмакның медианалары үзлеге
М—20	Турыпочмаклы өчпочмакта пропорциональ кисемтәләр
М—21	Охшашлык методы белән чишелә торган төзүгә мәсьәләләр
М—22	Турыпочмаклы өчпочмакта кысынкы почмакның синусы,
	косинусы, тангенсы һәм аларның 30', 45, 60 лы почмаклар
	өчен кыйммәтләре	66, 67
М—23	Турыпочмаклы өчпочмакларны чишү	66, 67
М—24*	Өчпочмаклар охшашлыгы	56—67
М—25	Туры һәм әйләнәнең үзара урнашуы
	Әйләнәгә орынма	68, 69
М—26	Камалган почмак турында теорема
М—27	Хорда кисемтәләренең тапкырчыгышы турында теорема
М —28*	Әйләнә	68—71
М—29	Өчпочмакның дүрт әһәмиятле ноктасы	72, 73
М—30	Камаулы әйләнә
М—31	Камаучы әйләнә
М—32	Вектор төшенчәсе	76—78
М—33	Векторларны кушу	77—81
М—34	Векторларны алу
М—35	Векторны санга тапкырлау
М—36	Векторларны мәсьәлә чишкәндә куллану
М—37	Трапециянең урта сызыгы
М—38	Йомгаклап кабатлау (дүртпочмаклар, мәйданнар, охшаш
	өчпочмаклар)
М—39	Йомгаклап кабатлау (әйләнә)
К—1	Дүртпочмаклар	39—47
К—2	Мәйдан	48—55
К—3	Охшаш өчпочмаклар	56—61
К—4	Охшашлыкны куллану, турыпочмаклы өчпочмакларны чишү	62—67
К—5	Әйләнә	68—75
К—6	Векторлар	76—84
К—7	Йомгаклап кабатлау

МӨСТӘКЫЙЛЬ ЭШЛӘР

1 нче вариант

М—1

1. Кабарынкы ABCDE бишпочмагының В түбәсе калган ике түбәсе белән тигез диагональләр ярдәмендә тоташтырылган. ZABE = ZCBD, ZBEA — ZBDC икәне билгеле булса, ABDE һәм BEDC дүртпочмакларының периметрлары тигез булу­ын исбатлагыз.

2. Почмаклары тигез булган кабарынкы тугызпочмаклык би­релгән. Бу почмакларны табыгыз.

М—2

1. ABCD дүртпочмагында АВ II CD, ВС II AD, AC = 20 см, BD = = 10 см, AB = 13 cm. Дүртпочмакның диагональләре О нокта­сында кисешәләр. COD өчпочмагының периметрын табыгыз.

2. Кысынкы почмагы А булган ABCD параллелограммының В түбәсеннән AD турысына ВК перпендикуляры төшерелгән; ВК = ^АВ булса, С һәм D почмакларын табыгыз.

М—3

1. Кабарынкы ABCD дүртпочмагында AB = CD, ZB = 70°, ZBCA = 60°, ZACD = 50°. ВС = AD булуын исбатлагыз.

2. Диаметры АС булган әйләнәдә BD кисемтәсенең уртасы шул әйләнәнең үзәге булып тора. Шул ук вакытта A, В, С, D нокталары бер туры өстендә ятмыйлар. ZABC = ZADC бу­луын исбатлагыз.

М—4

1. ABCD трапециясендә ВС — кечерәк нигез. AD кисемтәсендә, BE II CD булырлык итеп, Е ноктасы алынган; ZABE = 70°, ZBEA = 50°. Трапециянең почмакларын табыгыз.

2. Турыпочмаклы трапециянең кысынкы почмагы 45° ка тигез. Кечерәк ягы һәм кечерәк нигезе 10 ар см га тигез. Зуррак нигезне табыгыз.

1. Зур ягы, кечкенә диагонале һәм алар арасындагы почмак буенча параллелограмм төзегез.

2. Кечерәк нигезе һәм ян яклары буенча турыпочмаклы трапе­ция төзегез.

М—6

1. ABCD турыпочмаклыгында диагональләр О ноктасында кисешәләр. Е —АВ ягының уртасы, ABAC = 50°. EOD поч­магын табыгыз.

2. 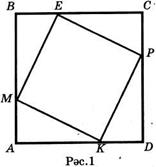АВ һәм CD диаметрлы әйләнә бирелгән. ACBD дүртпочма­гының турыпочмаклык икәнен исбатлагыз.

М—7

1. ABCD ромбында ZA = 31°. Диаго­нальләре О ноктасында кисешәләр. ВОС өчпочмагының почмакла­рын табыгыз.

2. 1 нче рәсемдә ABCD дүртпочма­гы — квадрат, АК = PD =ЕС = ВМ. Кабарынкы МЕРК дүртпочмагы­ның да квадрат булуын исбатлагыз.

М—8

1. Ягы һәм периметры буенча турыпочмаклык төзегез.

2. Ниндидер бер квадратның түбәсеннән диагоналенә төшерел­гән перпендикулярга тигез булган кисемтә бирелгән. Бу квадратны төзегез.

М—9

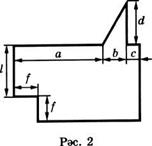
1. 2 нче рәсемдә сурәтләнгән фигу­раның мәйданын исәпләү өчен формула төзегез.

2. Турыпочмаклыкның периметры 26 см га, ә якларының берсе 9 см га тигез. Мәйданы шул турыпоч­маклыкныкы кадәр булган квад­ратның ягын табыгыз.

1. ABCD турыпочмаклыгында В почмагы җәенке. AD ягы­ның D түбәсе ягындагы дәвамында Z.ECD = 60°, Z.CED = 90°, AB = 4 cm, AD = 10 см булырлык итеп Е ноктасы билгелән­гән. Параллелограммның мәйданын табыгыз.

2. ABCD параллелограммында М һәм К нокталары тиңдәшле рәвештә ВС һәм AD ягының урталары. АВМК дүртпочма­гының мәйданы ACD өчпочмагының мәйданына тигез булуын исбатлагыз.

М—11

1. ABCD турыпочмаклыгында BD = 12 см. В түбәсе АС туры­сыннан 4 см ераклыкта ята. ABC өчпочмагының мәйданын табыгыз.

2. ABC өчпочмагында ZC = 135°, АС = 6 дм, BD биеклеге 2 дм га тигез. ABD өчпочмагының мәйданын табыгыз.

М—12

1. Тигезьянлы трапециянең периметры 32 см, ян ягы 5 см, мәйданы 44 см^{[1] [2] [3]}. Трапециянең биеклеген табыгыз.

2. ABCD трапециясенең AD һәм ВС нигезләре тиңдәшле рәвеш­тә 10 см һәм 8 см. ACD өчпочмагының мәйданы 30 см² булса, трапециянең мәйданын табыгыз.

М—13

1. Турыпочмаклы трапециянең зур диагонале 13 см га, ә зур­рак нигезе 12 см га тигез. Кечерәк нигезе 8 см га тигез булса, трапециянең мәйданын табыгыз.

2. Яклары 1, 73,2 булган өчпочмакның почмакларын табы­гыз.

1. AB, CD һәм EF, MN кисемтәләре бер-берсенә пропорциональ.

Әгәр АВ — 5 cm, CD = 80 мм, MN = 1 дм булса, EF ны табыгыз.

2. Турыпочмаклы АСВ өчпочмагында (ZC = 90°) АС = 6 см, ВС = 8 см, CD — биссектриса. АВ, AD, DB ны табыгыз.

М—16

1. ABC һәм DEF өчпочмаклары охшаш. ZA =AD, АС = AF, EF = = 14, DF = 2(J, ВС = 21. АС ягын табыгыз.

2. Охшаш ике өчпочмакның мәйданнары 16 см^{[4] [5]} һәм 25 см². Беренче өчпочмакның якларының берсе 2 см. Икенче өч­почмакта аңа охшаш якны табыгыз.

М—17

1. ABCD параллелограммында А түбәсе, аша ВС ягын Е нокта­сында, ә DC ягының дәвамын F ноктасында кисеп үтүче туры бирелгән. ААВЕсо AEFC булуын исбатлагыз.

2. ABC һәм AjBjCj өчпочмакларында АВ_Х = АС, АВ = АА_Х, АС = 2, В£_х = 4, А^ АВ дан 2,2 гә зуррак, AjBj = 2,8. Өчпоч­макның билгесез якларын табыгыз.

М—18

1. АВ һәм CD турылары О ноктасында кисешәләр,.

АСВО = ADAO булуын исбатлагыз.

2. 4 нче рәсемдә сурәтләнгән өчпочмакларның охшаш булуын исбатлагыз һәм АВ, DE турыларының үзара торышын ачык­лагыз.

В

М—19

1. Турыпочмаклы АСВ өчпочмагында (ZC = 90°) CD LAB,

= т,. ACD һәм CDB өчпочмаклары мәйданнарының ча­гыштырмасын табыгыз.

2. ABCD параллелограммында BD 1 AB, BE LAD, BE = 6 см, АЕ = 3 см. Параллелограммның мәйданын табыгыз.

М—21

1. Бирелгән А һәм С почмаклары һәм AM медианасы буенча ABC өчпочмагын төзегез.

2. Бирелгән кисемтәне 2:3:5 чагыштырмасында бүлегез.

М—22

1. Тигезьянлы трапециянең нигезләре 2 һәм 20 гә, ә ян ягы 15 кә тигез. Трапециянең кысынкы почмагының синусын, косинусын һәм тангенсын табыгыз.

2. АВ һәм CD — әйләнәнең үзара перпендикуляр булмаган ике диаметры, DE LAB, CD = 4, DE=>/3. Диаметрлар арасындагы кысынкы почмакны табыгыз.

М—23

1. Параллелограммның яклары а һәм b га, кысынкы почмагы а га тигез. Параллелограммның мәйданын табыгыз, а = 2,3, b — 3,7 а = 40°37' булганда, бу мәйданны исәпләгез.

2. Турыпочмаклы АСВ өчпочмагында (ZC = 90°) ZBAC = 45°, АВ = 10, D 6 ВС (В — D — С), ZDAC = 30°. DC ны табыгыз.

М—24*

1. Турыпочмаклы АСВ өчпочмагында (ZC = 90°) АС = 4, ВС = = 6, Е е АВ (А — Е —В), EFLBC, EDLAC; EF: ED = 1: 2. DEFC турыпочмаклыгының мәйданын табыгыз.

Зл/з

2. ABCD ромбында ZA = 60°, ә биеклеге —. АВ ягының В ноктасы ягындагы дәвамында, ВМ = 4 булырлык итеп, М ноктасы алынган. MD кисемтәсе ВС ны К ноктасында кисеп үтә. К ноктасы ВС кисемтәсен нинди чагыштырмада бүлә?

1. Турыпочмаклы АСВ өчпочмагында (ZC = 90°), АВ = 10, ААВС = 30°. Үзәге А ноктасында булган әйләнә үткәрелгән.

а) Әйләнә ВС турысына орынсын;

б) туры белән уртак нокталары булмасын;

в) ике уртак ноктасы булсын өчен әйләнәнең радиусы нинди булырга тиеш?

2. Әйләнәгә орынмада, орыну ноктасыннан ике якта, әйләнә үзәгеннән 20 см ераклыкта М һәм Т нокталары билгелән- гән. ТМ = 32 см. Әйләнәнең радиусын табыгыз.

М—26

1. Үзәге О ноктасында булган әйләнәнең АВ дугасы 60° ка ти­гез. Әйләнәнең радиусы 6 см га тигез булса, А ноктасыннан ОВ радиусына кадәр ераклыкны табыгыз.

2. АВ һәм АС — әйләнәнең хордалары. Z.BAC = 70°, оАВ = = 120°. АС дугасының градуслы үлчәмен табыгыз.

М—27

1. Түгәрәк эчендә урнашкан М ноктасы аша АВ һәм CD хор­далары үткәрелгән, AM = MB, CM = 16 см, DM: МС = 1: 4. АВ ны табыгыз.

2. АВ — әйләнәнең диаметры. С ноктасы әйләнә өстендә ята. CD ± АВ, AD = 3, DB = 5. CD ны табыгыз.

М—28*

1. Ике әйләнәнең үзәкләре уртак. Зуррак әйләнәнең радиусы R га, ә кечерәгенеке г га тигез. Кечерәк әйләнәгә орынучы зуррак әйләнә хордасының озынлыгын табыгыз.

2. Ике әйләнәнең радиуслары тигез, һәм алар А һәм В ноктала­рында кисешә. А ноктасы аша әйләнәләрнең берсен — С, ә икенчесен D ноктасында кисеп үтүче туры үткәрелгән. ВС = BD икәнен исбатлагыз.

М—29

1. Кысынкы почмаклы ABC өчпочмагында AD ± ВС, CF ± АВ, CF ны AD М ноктасында кисеп үтә. Z.ABM = Z.MCA икәнен исбатлагыз.

2. Турыпочмаклы АСВ өчпочмагында (ZC = 90°), АЕ — биссек­триса, СЕ = 5, АВ = 14. АВЕ өчпочмагының мәйданын табыгыз.

1. Әгәр өчпочмакның ягы 2л/3 см булса, тигезьяклы өчпоч­макка камаулы әйләнәнең радиусын табыгыз.

2. Әйләнәне камаучы тигезьянлы трапециянең периметры

10 см. Трапеция ягының озынлыгын табыгыз.

М—31

1. Тигезьянлы өчпочмакны камаучы әйләнә радиусы Зл/З кә тигез. Өчпочмакның периметрын табыгыз.

2. Радиусы 10 га тигез булган әйләнәгә катетларының берсе 16 га тигез булган турыпочмаклы өчпочмак камалган. Бу өчпочмакның мәйданын табыгыз.

М—32

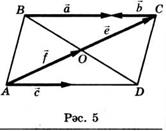
ABCD — параллелограмм. 5 нче рә­семдә сурәтләнгән:

а) коллинеар;

б) бердәй юнәлешле;

в) капма-каршы юнәлешле;

г) тигез векторлар парын күрсәтегез.

АС турысында, А ноктасыннан башлап, а га тигез булган вектор салып буламы?

М—33

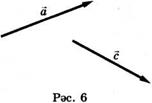
1. 6 нчы рәсемдә а һәм с векторлары сурәтләнгән, а+с векторын 2 ысул белән төзегез.

2. М, Н, Р, О, S — ирекле алынган нокталар. МН + РО + SM + HP + OS суммасын табыгыз.

М—34

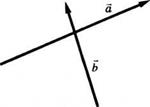
1.7 нче рәсемдә а һәм b векторлары сурәтләнгән, a — b векторын төзегез.

2. ABC өчпочмагы бирелгән. СВ век­торын АС һәм АВ векторлары аша күрсәтегез.

3.

Рәс. 7

Тигезьянлы ABC өчпочмагында М ноктасы — АС нигезенең уртасы. Әгәр АВ = 5 см, ВМ = 4 см булса, \МВ - МС+ВА\ ны табыгыз.

1. Коллинеар булмаган а һәм b векторлары бирелгән. 2а+ векторын төзегез.

2. ABCD параллелограммында О — диагональләр кисешү нок­тасы, К — CD ягының уртасы. ОА һәм АК векторларын АВ = а һәм AD-b векторлары аша күрсәтегез.

М—36

1. ABC өчпочмагында АА_г — медиана, М — АА₁ ягының урта­сы. ВМ векторын а = ВА һәм b = ВС векторлары аша күрсәтегез.

2. ABCD дүртпочмагында BC=^AD. Бу дүртпочмакның диа­гональләре кисешү ноктасында нинди чагыштырмада бүле­нәләр?

М—37

1. Трапеция нигезләренең аермасы 4 см га, ә урта сызыгы 10 см га тигез. Трапециянең нигезен табыгыз.

2. Тигезьянлы ABCD трапециясендә зуррак AD нигезенә В түбә­сеннән төшерелгән перпендикуляр аны 4 см га һәм 10 см га тигез булган 2 кисемтәгә бүлә. Трапециянең нигезләрен һәм урта сызыгын табыгыз.

М—38

ABCD — ягы 4 см га тигез булган квадрат. АВ һәм CD якла­рында AM = КС = 3 булырлык итеп, AM һәм КС кисемтәләре бирелгән.

а) MBKD — параллелограмм икәнлеген исбатлагыз.

б) Аның периметрын һәм мәйданын табыгыз.

М—39

1. Үзәге О ноктасында булган 10 см радиуслы әйләнәнең А ноктасы аша AM орынмасы үткәрелгән. ОМ кисемтәсе әйлә­нәне В ноктасында кисеп үтә. AM = 10л/3 см га тигез булса, иң кечкенә АВ дугасының градуслы үлчәмен табыгыз.

2. Бер ягы әйләнәнең үзәге аша үтәрлек, ә калган ике ягы аннан 3 см һәм ЗуЗ см га читтә ятарлык итеп, өчпочмакка әйләнә камалган. Әйләнәнең радиусын табыгыз.

2 иче вариант

М—1

1. ABCDEF кабарынкы алтыпочмагында AB = AF. А түбәсеннән ике үзара күрше булмаган түбәгә тигез диагональләр үткә­релгән, ABAC = AEAF. АВСЕ һәм ACEF дүртпочмаклары­ның периметрлары тигез икәнен исбатлагыз.

2. Почмаклары суммасы 540° ка тигез булган кабарынкы күп­почмакның ничә ягы бар?

М—2

1. ABCD дүртпочмагында AB II CD, ВС II AD, О — диагональләре кисешү ноктасы. AOD өчпочмагының периметры 25 см га тигез, АС — 16 см, BD = 14 см. ВС ны табыгыз.

2. А почмагы кысыныкы булган ABCD параллелограммы би­релгән. В түбәсеннән AD турысына ВК перпендикуляры төшерелгән, АК = ВК. АС һәм AD ны табыгыз.

М—3

1. ABCDEP кабарынкы алтыпочмагының барлык яклары да тигез һәм АА — AD. BP II СЕ икәнен исбатлагыз.

2. ABCD параллелограммы бирелгән. АС диагоналенең дәва­мында А һәм С түбәләре ягында, AA_t = СС_Г булырлык итеп, Aj һәм С) нокталары билгеләнгән. ABA_XD = ABC_rD икәнен исбатлагыз.

М—4

1. МНРК трапециясендә МК — зур нигез. МН һәм РК турыла­ры Е ноктасында кисешәләр, АМЕК = 80°, АЕНР= 40°. Трапециянең почмакларын табыгыз.

2. Турыпочмаклы трапециянең кысынкы почмагы 60° ка тигез. Зур ягы һәм зур нигезе 20 шәр см га тигез. Трапециянең кечкенә нигезен табыгыз.

М—5

1. Кечкенә ягы, кысынкы почмагы һәм бу ягы белән кечкенә диагонале арасындагы почмагы буенча параллелограмм төзегез.

2. Кечкенә диагонале, зур нигезе һәм зур ягы буенча турыпоч­маклы трапеция төзегез.

 

1. МРКН турыпочмаклыгының диагональләре О ноктасында кисешәләр. ОА кисемтәсе МОР өчпочмагының биеклеге, ZAOP = 15°. ОНК почмагын табыгыз.

2. А почмагы кысынкы булган ABCD параллелограммының диагональләре О ноктасында кисешәләр. АО һәм ОС кисем­тәләрендә тиңдәшле рәвештә Р һәм К нокталары алынган, OP = OD, OK = OB. PBKD дүртпочмагының турыпочмаклык булуын исбатлагыз.

М—7

1. К почмагы җәенке булган МРКН ромбының диагональләре Е нокта­сында кисешәләр. РКЕ өчпочма­гының бер почмагы 16°30'ка ти­гез. Бу өчпочмакның калган поч­макларын һәм РМН почмагын табыгыз.

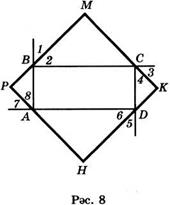
2. 8 нче рәсемдә бирелгән ABCD дүрт­почмагы — турыпочмаклык, би­редә Z1 = Z2, Z3 = Z4, Z5 = Z 6, Z7 =Z8. МКНР кабарынкы дүрт­почмагының квадрат булуын ис­батлагыз.

М—8

1. Җәенке почмагы һәм кечкенә диагонале буенча ромб төзегез.

2. Ниндидер бер квадратның диагональләре кисешү ноктасын­нан аның бер ягына төшерелгән перпендикулярга тигез кисемтә бирелгән. Бу квадратны төзегез.

М—9

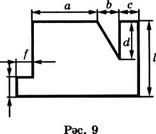*1. 9 нчы рәсемдә сурәтләнгән фигу­раның мәйданын исәпләү өчен формула төзегез.

2. Квадратның периметры 32 см га, ә турыпочмаклыкның бер ягы 4 см га тигез. Әгәр турыпочмак­лыкның мәйданы квадратныкы кадәр булса, турыпочмаклыкның икенче ягын табыгыз.

1. МРКТ параллелограммының МТ ягында Е ноктасы билге­ләнгән, АРЕМ = 90°, АЕРТ = 45°, ME = 4 см, ЕТ = 7 см. Параллелограммның мәйданын табыгыз.

2. ABCD параллелограммында М, Р, К, Т нокталары — тиңдәшле рәвештә AB, ВС, CD, AD якларының урталары. АВРТ һәм AMKD дүртпочмакларының мәйданнары тигез икәнен исбатлагыз.

М—11

1. Гипотенузасы 10 см га тигез булган тигезьянлы турыпоч­маклы өчпочмакның мәйданын табыгыз.

2. Мәйданы 36 см^{[6] [7] [8] [9]} булган ABC өчпочмагының АС ягында, AD: DC = 1:5 булырлык итеп, D ноктасы алынган. ABD өчпочмагының мәйданын табыгыз.

М—12

1. Турыпочмаклы трапециянең мәйданы 30 см², периметры 28 см, ә кечерәк ягы 3 см. Трапециянең зуррак ягын табыгыз.

2. МРКТ трапециясенең кечкенә нигезе РК = 6 см, ә биек­леге 8 см. Әгәр МКТ өчпочмагының мәйданы 48 см² булса, трапециянең мәйданын табыгыз.

М—13

1. Турыпочмаклы трапециянең нигезләре 9 см һәм 18 см, ә зуррак ягы 15 см га тигез. Трапециянең мәйданын табыгыз.

2. Яклары 1, 1, 72 булган өчпочмакның почмакларын табыгыз.

М—14

1. 10 нчы рәсемдә сурәтләнгән фигураны җ—i————г-д

дәфтәрегезгә күчереп сызыгыз. Кирәкле ____ ——L

үлчәүләрне башкарып, фигураның мәйда- \ __ /

нын исәпләгез. Г^- Т

2. МРКН турыпочмаклыгының РК ягында — - V--------------- г~

Е ноктасы билгеләнгән, ME =15 см, ________ I М I I I—

РМ = 12 см, ЕК = 6 см. МЕКН дүртпоч­

магының мәйданын табыгыз. ^Рәс' ¹⁰

1. KPF һәм EMT өчпочмаклары охшаш, биредә,

ZF = 20°, АЕ= 40°. Бу өчпочмакларның калган почмакла­рын табыгыз.

2. Охшаш өчпочмакларның ике охшаш ягы 2 см һәм 5 см га тигез. Беренче өчпочмакның мәйданы 8 см². Икенче өчпоч­макның мәйданын табыгыз.

М—17

1. Параллелограммның С түбәсе аша AD ягын Е ноктасында, ә ВА ягының дәвамын F ноктасында кисеп үтүче туры үткә­релгән. AECD co &FBC икәнен исбатлагыз.

2. ДВС һәм DEF өчпочмакларында ZA = АЕ, AC = AF, АС = 6, EF = 2, АВ = 3,3 һәм DF ягының ВС ягыннан 3,2 гә кечерәк икәне билгеле. Өчпочмакның билгесез якларын табыгыз.

М—18

1. ABCD параллелограммы бирелгән. Е, F, М, N нокталары тиң­дәшле рәвештә параллелограммның АВ, ВС, CD, AD якларын­да яталар, ⁼ 7^. ABEF = ANMD _в

булуын исбатлагыз. 2, 5^^4 д ________ 20 _____ Е

2. 11 нче рәсемдә сурәтләнгән өчпоч- A 5 с ~7

макларның охшаш булуын исбат- /ю

лагыз һәм ВС һәм DF турылары-

ның үзара торышын ачыклагыз. _Рәс ц ^F

М—19

1.0 — ABCD ромбы диагональләренең кисешү ноктасы, ә Е һәм F — ВС, DC якларының урталары. EF = ВО һәм EF LAC булуын исбатлагыз.

2. МРК өчпочмагының медианалары кисешү ноктасы аша МК ягына параллель CD кисемтәсе үткәрелгән (С е MP, D g РК), CD = 18 см. МК ягын табыгыз.

М—20

1. Турыпочмаклы АСВ өчпочмагында (АС = 90°) CD.LAB,

AD _2 икәне билгеле. ADC һәм АСВ өчпочмакларының АС 3 мәйданнары чагыштырмасын табыгыз.

2. ABCD — турыпочмаклы трапеция (AD = АС = 90°), ВС = 3, CD — 6, BD ± АВ. Трапецияңнң мәйданын табыгыз.

1. Бирелгән С почмагы, ике ягының чагыштырмасы АС: СВ = 2:3 һәм CD биссектрисасы буенча ABC өчпочмагын төзегез.

2. Бирелгән кисемтәне 1:4:7 чагыштырмасында бүлегез.

М—22

1. Турыпочмаклы АСВ өчпочмагында (ZC = 90°) CD ± АВ, AD = 2, DB = 3, А почмагының синусын, косинусын һәм тангенсын табыгыз.

2. ABCD турыпочмаклы трапеция (ZD = ZC = 90°), ВС = 2, AD - 4,

CD = 2л/3. А почмагын табыгыз.

М—23

1. Ромбның биеклеге һ, ә кысынкы почмагы а. Ромбның мәй­данын табыгыз. Әгәр һ = 17,3, а = 52°43' булса, бу мәйдан­ны исәпләгез.

2. ABC өчпочмагында ZA = 60°, Z.C = 45°, BD ± AC, AD = 3. ВС ягын табыгыз.

М—24*

1. Турыпочмаклы АСВ өчпочмагында (ZC = 90°) D е АВ

(A — D — B),DE 1 ВС, DE = 3, DC = 5, AC = 2ВС. ABC өч­почмагының мәйданын табыгыз. _г

2. ABCD турыпочмаклыгының АС диагонале кә тигез һәм AD ягы белән 30° лы почмак төзи. AD ягы D ноктасы ягына 3 кә тигез булган DE кисемтәсенә дәвам ителгән. BE кисемтәсе CD ягын К ноктасында кисеп үтә. BE кисемтәсе CD ягын нинди чагыштырмада бүлә?

М—25

1. ABCD квадратында АС = 10л/2, ә О — AD ягының уртасы. Үзәге О ноктасында булган әйләнә үткәрелгән.

а) Әйләнә АВ һәм CD турыларына орынсын;

б) турылар белән әйләнәнең уртак ноктасы булмасын;

в) һәрбер туры белән икешәр уртак ноктасы булсын өчен, әйләнәнең радиусы нинди булырга тиеш?

2. Әйләнәгә үткәрелгән орынманың орыну ноктасы С дан аның ике ягына СА һәм СВ кисемтәләре салынган, биредә ZAOC = = ZBOC (О — әйләнә үзәге). Әйләнә үзәге 8 гә тигез, АВ = 30. Әйләнә үзәгеннән А һәм В нокталарына кадәр булган ераклыкны табыгыз.

1. Үзәге О ноктасында булган әйләнәдә, А ноктасыннан О В радиусына кадәр ераклык радиус озынлыгыннан 2 тапкырга кечерәк булырлык итеп, ОА һәм ОВ радиуслары үткәрелгән. АВ дугасының градуслы үлчәмен табыгыз.

2. Әйләнәдә АВ диаметры һәм АС хордасы үткәрелгән. Әгәр АС һәм СВ дугаларының градуслы үлчәмнәренең чагыш­тырмасы 7: 2 булса, ВАС почмагын табыгыз.

М—27

1. Әйләнәнең АВ һәм CD хордалары Е ноктасында кисешәләр. АЕ: ЕВ = 1:3, CD = 20, DE = 5. АВ хордасын табыгыз.

2. АВ — әйләнәнең диаметры. Е ноктасы әйләнә өстендә ята. EF ± АВ, ЕВ = 4, EF = 6. Әйләнәнең радиусын табыгыз.

М—28*

1. АВ — үзәге О ноктасында булган әйләнә диаметры. ОВ ки­семтәсен диаметр итеп алып, г радиуслы әйләнә үткәрелгән. А ноктасы аша кечкенә әйләнәгә АК орынмасы үткәрелгән. (К — орыну ноктасы.) АК ны табыгыз.

2. Әйләнәдә А, В, С, D нокталары билгеләнгән. иВС = uAD. АВ II CD икәнен исбатлагыз.

М—29

1. Турыпочмаклы ABC өчпочмагында (ZC = 90°) р — АВ ягына төшерелгән урта перпе<