А.В. Шевкин, ФМШ 2007
Рассмотрим несколько задач на нахождение наибольшего значения некоторой величины. Вот первая задача из сборника тренировочных заданий к ЕГЭ-2016.
1. У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель или свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 300 ц/га, а на втором — 200 ц/га. Урожайность свёклы на первом поле составляет 200 ц/га, а на втором — 300 ц/га за центнер. Фермер может продавать картофель по 10000 руб. за центнер, а свёклу — по цене 13000 руб. Какой наибольший доход может получить фермер?
Решение. Пусть на первом поле занято x га картофелем и (10 – x)га свёклой, на втором поле y га занято картофелем и (10 – y)га свёклой. Тогда доход вычисляется по формуле:
 =
= 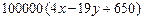 .
.
Очевидно, что доход будет наибольшим при наибольшем возможном x = 10 и наименьшем возможном y = 0. Наибольший доход равен 69000000 руб.
Эту задачу можно решить "по-нашему, по-неучёному", как говаривал Удодов-старший из рассказа А.П.Чехова "Репетитор".
На первом поле 1 га, занятый картофелем, приносит 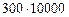 руб. дохода, а 1 га, занятый свёклой, приносит
руб. дохода, а 1 га, занятый свёклой, приносит  руб., что меньше На первом поле выгоднее сажать картофель. На втором поле 1 га, занятый картофелем, приносит
руб., что меньше На первом поле выгоднее сажать картофель. На втором поле 1 га, занятый картофелем, приносит  руб. дохода, а 1 га, занятый свёклой, приносит
руб. дохода, а 1 га, занятый свёклой, приносит 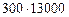 руб., что больше. На втором поле выгоднее сажать свёклу. Наибольший доход составляет
руб., что больше. На втором поле выгоднее сажать свёклу. Наибольший доход составляет  = 69000000 руб.
= 69000000 руб.
Теперь рассмотрим две задачи из того же сборника с другим сюжетом.
2. В двух шахтах добывают алюминий и никель. В первой шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1 кг алюминия или 3 кг никеля. Во второй шахте имеется 300 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 3 кг алюминия или 1 кг никеля. Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
Решение. Пусть на первой шахте x рабочих добывают алюминий и (100 – x) рабочих добывают никель. В день они добывают 5 x кг алюминия и 15(100 – x) кг никеля.
Пусть на второй шахте y рабочих добывают алюминий и (300 – y) рабочих добывают никель. В день они добывают 15 y кг алюминия и 5(300 – y) кг никеля.
Пусть весь добытый металл сплавили и получилось отношение масс 2: 1, тогда верно равенство:
5 x + 15 y = 2(15(100 – x) + 5(300 – y)),
откуда получим, что
y = 240 – 1,4 x. (1)
Теперь вычислим массу m полученного сплава:
m = 5 x + 15 y + 15(100 – x) + 5(300 – y) = 10(300 + y – x),
откуда получим, что
y = x + 0,1 m – 300. (2)
Итак, пара целых чисел x и y удовлетворяет уравнениям (1) и (2). Точка (x; y) принадлежит точечным графикам функций — убывающей (1) и возрастающей (2). При этом наибольшее значение m достигается при x = 0. Тогда y = 240, m = 5400.
Ответ. 5400 кг.
В следующей задаче отношения между известными и неизвестными величинами более сложные.
3. В двух областях есть по 50 рабочих, каждый из которых готов трудиться 10 часов в сутки на добыче алюминия и никеля. В первой области один рабочий за час добывает 0,2 кг алюминия или 0,1 кг никеля. Во второй области для добычи x кг алюминия в день требуется x 2 человеко-часов труда, а для добычи y кг никеля в день требуется y 2 человеко-часов труда. Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 1 кг алюминия приходится 2 кг никеля. При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
Решение. Пусть в первой области y рабочих добывают алюминий и (50 – y) рабочих добывают никель. В день они добывают 2 y кг алюминия и (50 – y) кг никеля.
Пусть во второй области за сутки добывают x кг алюминия, затрачивая x 2 человеко-часов труда. Тогда алюминий добывают 0,1 x 2 рабочих, а никель добывают (50 – 0,1 x 2) рабочих, затрачивая (500 – x 2) человеко-часов труда и добывая  кг никеля.
кг никеля.
Пусть весь добытый металл сплавили и получилось отношение масс 2: 1, тогда верно равенство:
(50 – y) +  = 2(2 y + x),
= 2(2 y + x),
откуда получим, что
y = 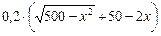 . (3)
. (3)
Теперь вычислим массу m полученного сплава:
m = (50 – y) +  + 2 y + x = 50 +
+ 2 y + x = 50 +  + y + x,
+ y + x,
откуда, подставив выражение 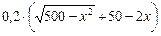 вместо y получим, что
вместо y получим, что
m = 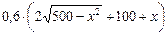 .
.
Рассмотрим непрерывную функцию m (x) = 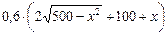 , определённую на отрезке [0; 10
, определённую на отрезке [0; 10  ] и дающую значения величины m из нашей задачи для целых значений x из указанного отрезка.
] и дающую значения величины m из нашей задачи для целых значений x из указанного отрезка.
Производная функции m (x) равна m' (x) = 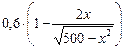 . На указанном отрезке функция m (x) имеет единственную критическую точку x 0 = 10. Эта точка является точкой максимума, так как m' (5) > 0, а m' (20) < 0. Так как m (10) = 90, то наибольшая масса сплава равна 90 кг.
. На указанном отрезке функция m (x) имеет единственную критическую точку x 0 = 10. Эта точка является точкой максимума, так как m' (5) > 0, а m' (20) < 0. Так как m (10) = 90, то наибольшая масса сплава равна 90 кг.
Ответ. 90 кг.
Надо признать, что решение получилось уж очень "взрослое", поэтому я обратился к коллеге Ю.А. Пукасу, и он нашёл возможность его упростить.
Если массу добытого алюминия обозначить 2 y + x = a (a = 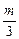 ), то, подставив в равенство
), то, подставив в равенство
(50 – y) +  = 2(2 y + x)
= 2(2 y + x)
a вместо 2 y + x и  вместо y, перепишем его в виде:
вместо y, перепишем его в виде:
2  = 5 a – x – 100.
= 5 a – x – 100.
Возведя это равенство в квадрат, после упрощения получим квадратное уравнение относительно x:
 .
.
Чтобы наша задача имела решение, это уравнение должно иметь неотрицательный дискриминант:

что даёт нам границы для a:

При наибольшем значении a = 30 из этого промежутка квадратное уравнение имеет единственный корень x = 10. При этом получается наибольшее значение m = 90.
Таким образом, нашлось решение задачи 3 без производной.
Конечно же хочется найти решение попроще, совсем "детское". Оно существует, но годится больше для перепроверки полученного результата, так как существенно опирается на условие "число x целое", а этого условия в задаче нет. Рассмотрим и это "решение".
Как мы видели выше, во второй области алюминий и никель добывают 0,1 x 2 и
(50 – 0,1 x 2) рабочих соответственно. Так как эти величины целые и неотрицательные, то если число x целое, то из делимости x 2 на 10 следует, что x делится на 10 (это надо доказать). Чтобы число (50 – 0,1 x 2) оставалось неотрицательным, x может быть равен только 0, 10, 20.
Проверкой убеждаемся, что из этих трёх значений лишь x = 10 удовлетворяет условиям задачи и приводит к тому же ответу.
Приведённое выше "детское решение" задачи не является настоящим решением задачи, так как условие "число x целое" не дано в её условии. Чтобы числа 0,1 x 2 и
(50 – 0,1 x 2) оставались неотрицательными целыми числами в качестве x 2 нужно брать числа 0, 10, 20, …, 500, тогда в качестве x можно брать числа 0, 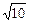 ,
, 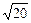 , …,
, …,  . При этом число y в формуле (3) должно быть целым, что возможно лишь при тех же значениях x: 0,
. При этом число y в формуле (3) должно быть целым, что возможно лишь при тех же значениях x: 0,  ,
,  , для которых ответ уже получен выше.
, для которых ответ уже получен выше.
Так как есть риск пройти мимо этого тонкого места и выбор трёх значений x из 51 могут посчитать необоснованным, то "детское решение" на экзамене лучше не использовать.
Для разнообразия рассмотрим задачу 19 из ЕГЭ-2015, в ней требовалось найти наименьшее значение величины.
4. Владимир является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t 2 часов в неделю, то за эту неделю они производят 2 t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t 2 часов в неделю, то за эту неделю они производят 5 t единиц товара. За каждый час работы (на каждом из заводов) Владимир платит рабочему 500 рублей. Владимиру нужно каждую неделю производить 580 единиц товара. Какую наименьшую сумму придётся тратить еженедельно на оплату труда рабочих?
Решение. Пусть на заводе в первом городе рабочие трудятся суммарно t 2 часов в неделю и производят 2 t единиц товара, а на заводе во втором городе рабочие трудятся суммарно x 2 часов в неделю и производят 5 x единиц товара. Тогда верно равенство
2 t + 5 x = 580,
откуда 2 t = 580 – 5 x.
Сумма, расходуемая на оплату труда равна

 .
.
Эта сумма будет наименьшей, если квадратичная функция 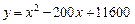 принимает наименьшее значение, то есть в точке x = 100 (абсцисса вершины параболы).
принимает наименьшее значение, то есть в точке x = 100 (абсцисса вершины параболы).
Итак, наименьшая сумма равна 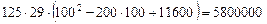 руб.
руб.
Ответ. 5800000.
Рассмотрим ещё две задачи на нахождение наибольшего значения величины с применением совсем другой идеи. Возможно, эта идея будет использована в будущих экзаменах, когда решат, что надо не упрощать, а усложнять их. Первую из задач можно разобрать на уроке, а за самостоятельное решение второй задачи вполне можно поставить "пятёрку".
5. Цех кондитерской фабрики производит шоколадные батончики двух сортов массой 50 г в коробках по 24 батончика: «Шоколадный» (50 % шоколада и 25 % орехов) и «Ореховый» (40 % шоколада и 50 % орехов). Цех получает прибыль от реализации коробки батончиков сортов «Шоколадный» и «Ореховый» в сумме 240 р. и 300 р. соответственно. Какую наибольшую прибыль (в рублях) может получить цех, если за смену он может израсходовать не более 108 кг шоколада и 90 кг орехов?
Решение. Масса батончиков в одной коробке составляет  (г). Коробка сорта «Шоколадный» содержит 600 г шоколада и 300 г орехов, а коробка сорта «Ореховый» содержит 480 г шоколада и 600 г орехов.
(г). Коробка сорта «Шоколадный» содержит 600 г шоколада и 300 г орехов, а коробка сорта «Ореховый» содержит 480 г шоколада и 600 г орехов.
Пусть цех произвел x коробок батончиков сорта «Шоколадный» и y коробок батончиков сорта «Ореховый», тогда цех израсходовал 600 x + 480 y г шоколада и
300 x + 600 y г орехов, а прибыль от реализации произведённой продукции составит
p = 240 x + 300 y р.
Наибольшая прибыль получится в том случае, если будет произведено целое количество коробок каждого сорта и будет израсходован весь запас шоколада и орехов, который можно израсходовать.
Решим систему уравнений 600 x + 480 y = 108000 и 300 x + 600 y = 90000.
Эта система имеет единственное решение: x = 100 и y = 100. Увеличить количество коробок нельзя, так как весь шоколад и все орехи уже израсходованы. Наибольшая прибыль от реализации произведённой продукции составит p = 240 x + 300 y = 54000 (р.).
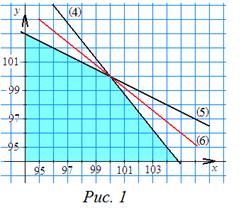
Замечание. Рассмотрим графическую иллюстрацию приведённого выше решения.
По условию задачи должны выполняться неравенства
600 x + 480 y  108000 и 300 x + 600 y
108000 и 300 x + 600 y  90000,
90000,
которые перепишем в виде: y  225 –
225 –  x и y
x и y  150 –
150 – 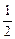 x.
x.
Любая пара натуральных чисел (x; y), удовлетворяющая этим неравенствам изображается точкой, лежащей не выше каждой из прямых
 y = 225 –
y = 225 –  x, (4)
x, (4)
y = 150 – 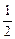 x, (5)
x, (5)
то есть точкой, принадлежащей области, закрашенной на рисунке 1.
Из равенства p = 240 x + 300 y выразим y через p и x:
y = 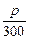 –
–  x. (6)
x. (6)
Меняя значения p, получим семейство параллельных прямых. Одна из этих прямых — прямая (6) на рисунке (p = 54000) — проходит через точку пересечения прямых (4) и (5). Прямые рассматриваемого семейства параллельных прямых, проходящие через точки (x; y), закрашенной области, проходят ниже прямой (6), так как все эти точки расположены ниже прямой (6). Этим прямым соответствуют значения p < 54000.
Ответ. 54000.
6. Другой раз тот же цех кондитерской фабрики должен был произвести шоколадные батончики двух сортов при тех же условиях. Какую наибольшую прибыль (в рублях) может получить цех, если на смену он получает не более 120 кг шоколада и 99 кг орехов?
Решение. Рассуждая как при решении предыдущей задачи, получим неравенства
600 x + 480 y  120000 и 300 x + 600 y
120000 и 300 x + 600 y  99000,
99000,
которые перепишем в виде: y  250 –
250 –  x и y
x и y  165 –
165 – 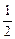 x.
x.
 Любая пара натуральных чисел (x; y), удовлетворяющая этим неравенствам изображается точкой, лежащей не выше каждой из прямых
Любая пара натуральных чисел (x; y), удовлетворяющая этим неравенствам изображается точкой, лежащей не выше каждой из прямых
y = 250 –  x, (7)
x, (7)
y = 165 – 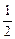 x, (8)
x, (8)
Эти точки с целыми координатами принадлежат области, закрашенной на рисунке 2.
Из равенства p = 240 x + 300 y выразим y через p и x, получим равенство (6). Рис. 2
Меняя значения p, получим семейство параллельных прямых. Одна из этих прямых — прямая (6) — на рисунке 2 проходит через точку пересечения прямых (7) и (8), но координаты этой точки пересечения — дробные числа.
Найдём наибольшее значение p, при котором прямая, задаваемая уравнением
y = 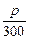 –
–  x, проходит через точку с целыми координатами (на рисунке 2 эти точки выделены). Эта точка имеет координаты (112; 109). Найдём значение p, соответствующее значениям x = 112 и y = 109:
x, проходит через точку с целыми координатами (на рисунке 2 эти точки выделены). Эта точка имеет координаты (112; 109). Найдём значение p, соответствующее значениям x = 112 и y = 109:
p = 240 x + 300 y = 240 × 112 + 300 × 109 = 59580 (р.).
Значение p = 59580 является наибольшим, так как точки с целыми координатами из закрашенной области лежат ниже прямой y =  –
–  x.
x.
Ответ. 59580.