Сервис, Поиск решения...

Методы решения задач

3.1.1. Постановка задачи

Задача линейного программирования, которая является частным случаем задачи оптимизации (1.1.9), записывается следующим образом:

(3.1.1)

Задача линейного программирования является достаточно распространенной задачей принятия оптимальных решений, особенно в экономике. Решение этой задачи рассмотрим на примере задачи распределения ресурсов. Но сначала маленькое отступление.

Чтобы смотреть телевизор, совсем не обязательно иметь представление о принципах его работы. Большинство авиапассажиров не знает, что такое подъемная сила и почему самолеты летают на больших высотах. Точно так же, чтобы принимать оптимальное решение на основе математической модели, совершенно не обязательно знать достаточно сложные алгоритмы, по которым это решение находится.

С другой стороны, когда известно, каким путем получен результат, больше уверенности в его правильности и на душе спокойнее. Поэтому любознательному читателю мы предоставляем возможность познакомиться с алгоритмами решения задач линейного программирования.

Задачу линейного программирования можно решать аналитическими и графическими методами. Аналитические методы, которые представляют собой последовательность вычислений по некоторым правилам, являются основой для решения задачи на компьютере. Их единственный недостаток заключается в том, что в отличие от графических методов, они совершенно не наглядны. Графические же методы достаточно наглядны, но они пригодны лишь для решения таких задач, в которых число переменных n = 2, что дает возможность представлять задачу на плоскости. Однако, учитывая наглядность графических методов, идею решения задачи линейного программирования мы рассмотрим с их помощью.

Начнем с простых примеров.

Как известно, уравнение прямой имеет вид

a₁x₁+a₂x₂=b. (3.1.2)

Построим прямую

2х₁+х₂=2.

Для этого запишем уравнение в виде

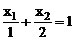. (3.1.3)

При такой форме записи в знаменателе показаны отрезки, которые отсекает прямая (3.1.3) на осях координат, что показано на рис. 3.1.1.

Если от уравнения (3.1.2) перейти к неравенству

2х₁+х₂ £ 2, (3.1.4)

то его можно представить графически, как это показано на рис. 3.1.2.

Из приведенных рисунков видно, что если линейное уравнение с двумя неизвестными представляет собой прямую линию, то линейное неравенство — полуплоскость.

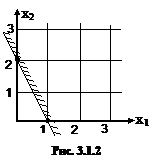На рис. 3.1.2 часть плоскости, которая не удовлетворяет неравенству и расположена выше прямой, заштрихована. Координаты всех точек, принадлежащихне заштрихованной части плоскости, имеют такие значения x₁ и x_2, которые удовлетворяют заданному неравенству. Эта полуплоскость является областью допустимых решений (ОДР).

Построим теперь систему неравенств:

(3.1.5)

х₁ ³ 0; х₂ ³ 0

Для удобства построения запишем ее в форме уравнения в отрезках:

(3.1.6)

Эта система построена на рис. 3.1.3, из которого следует, что решением этой системы являются координаты всех точек, принадлежащих ОДР, т. е. многоугольнику АВCDO.

Поскольку в ОДР бесчисленное множество точек, значит, рассматриваемая система имеет бесчисленное множество допустимых решений.

Если мы хотим найти оптимальное решение, то должны принять целевую функцию. Допустим, мы хотим, чтобы решение было оптимальным в смысле максимизации целевой функции

(3.1.7)

Эта зависимость на рис 3.1.4 представлена в форме уравнения прямой с угловым коэффициентом

х₂ = F - x_1,

из которого видно, что tga = -1. При этом угол a = 135°, а величина F равна отрезку, отсекаемому прямой на оси координат. Если прямую перемещать параллельно самой себе в направлении, указанном стрелками, то величина F будет возрастать. Совместим теперь ОДР, изображенную на рис. 3.1.3, с линией целевой функции (3.1.7), построенной на рис. 3.1.4, как это показано на рис. 3.1.5.

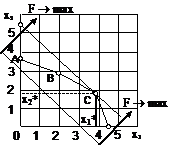
Рис. 3.1.5

Поскольку требуется найти оптимальное решение, при котором целевая функция

,

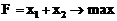т. е. стремится к максимуму, будем перемещать график целевой функции в направлении увеличения F. Очевидно, что оптимальным решением будут координаты точки С, равные х₁* и х₂*. При этом F = F*.

На основании рассмотренного можно сделать исключительно важный вывод: оптимальным решением являются координаты вершины ОДР.

На этом выводе базируется аналитический метод решения задач линейного программирования, который заключается в следующем:

rНайти вершины ОДР, как точки пересечения ограничений.

rОпределить последовательно значения целевой функции
в вершинах.

rВершина, в которой целевая функция приобретает оптимальное (максимальное или минимальное) значение, является оптимальной вершиной.

rКоординаты этой вершины и являются искомыми оптимальными значениями переменных.

Эти правила, сформулированные на основании графического решения задачи на плоскости, т. е. в двухмерном пространстве, справедливы и для трехмерного. В этом случае ОДР представляет собой многогранник. Координаты каждой его вершины — это допустимые решения. Координаты той вершины, в которой целевая функция имеет максимальное (или минимальное) значение, являются оптимальным решением задачи. Для трехмерного пространства, где число переменных равно трем, это нетрудно себе представить. В практических же задачах число переменных может исчисляться десятками и даже сотнями. В этом случае никакое пространственное воображение не поможет. Что же делать? А выход один — решать задачу аналитически.

Но чтобы читатель не думал, что мы занимаемся чистой теорией, прервем ненадолго теоретические рассуждения и рассмотрим содержательную сторону типовой задачи линейного программирования.

3.1.2. Задача распределения ресурсов

Если финансы, оборудование, сырье и даже людей полагать ресурсами, то значительное число задач в экономике можно рассматривать как задачи распределения ресурсов. Достаточно часто математической моделью таких задач является задача линейного программирования.

Рассмотрим следующий пример.

Требуется определить, в каком количестве надо выпускать продукцию четырех типов Прод1, Прод2, Прод3, Прод4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье, финансы. Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены на рис. 3.1.6. Там же приведено наличие располагаемого ресурса.

Рис. 3.1.6

Составим математическую модель, для чего введем следующие обозначения:

х_j — количество выпускаемой продукции j-го типа, ;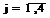

b_i — количество располагаемого ресурса i-го вида, ;

a_ij — норма расхода i-го ресурса для выпуска единицы продукции j-го типа;

c_j — прибыль, получаемая от реализации единицы продукции j-го типа.

Теперь приступим к составлению модели.

Как видно из рис. 3.1.6, для выпуска единицы Прод1 требуется 6 единиц сырья, значит, для выпуска всей продукции Прод1 требуется 6х₁ единиц сырья, где х₁ — количество выпускаемой продукции Прод1. С учетом того, что для других видов продукции зависимости аналогичны, ограничение по сырью будет иметь вид:

6х₁+5х₂+4х₃+3х₄ £ 110.

В этом ограничении левая часть равна величине потребного ресурса, а правая показывает количество имеющегося ресурса.

Аналогично можно составить ограничения для остальных ресурсов и написать зависимость для целевой функции. Тогда математическая модель задачи будет иметь вид:

(3.1.8)

Задачу, имеющую 4 переменных, представить на плоскости, как мы уже знаем, невозможно, поэтому познакомимся с аналитическим методом решения таких задач.

3.1.3. Основные положения симплекс-метода

Для решения рассматриваемой задачи вернемся к теории.

Идея аналитического решения таких задач заключается, как мы уже говорили, в последовательном переборе вершин, в одной из которых и находится оптимальное решение.

Для аналитического решения задач линейного программирования разработан специальный алгоритм направленного перебора вершин. Этот алгоритм обеспечивает переход от одной вершины к другой в таком направлении, при котором значение целевой функции от вершины к вершине улучшается.

В геометрии есть такое понятие "симплекс". Симплексом тела в k-мерном пространстве называют совокупность k+1 его вершин. Так, для плоскости при к = 2 симплексом будут три вершины треугольника, при к = 3 — четыре вершины четырехгранника и т. д. С учетом этого понятия аналитический метод решения задачи линейного программирования называют симплекс-методом. Вычисления, обеспечивающие определение значения целевой функции и переменных в одной вершине, называются итерацией.

Аналитическое решение задачи линейного программирования — дело весьма сложное, поэтому подробно описывать его не будем, а изложим лишь те его основные идеи, которые реализованы в Excel.

Решение задачи с помощью симплекс-метода будем рассматривать на примере задачи, математическая модель которой имеет вид (3.1.8).

По сравнению с системой (3.1.8) в системе (3.1.9) введены дополнительные переменные у_i и выполнен переход от системы неравенств к системе уравнений. Следует подчеркнуть, что с точки зрения содержания величина у_i равна величине неиспользованного ресурса.

(3.1.9)

Систему (3.1.9) перепишем в следующем виде:

(3.1.10)

Систему (3.1.10) можно представить в виде таблицы, приведенной на рис. 3.1.7.

Рис. 3.1.7

Таблица (рис. 3.1.7) называется симплекс-таблицей и является основной формой решения задачи линейного программирования. В этой таблице все переменные делятся на свободные и базисные. Свободные переменные находятся в ячейках С3:F3, базисные — в ячейках А5:А7. Если переменная свободная, то ее значение равно нулю. На рис. 3.1.7 все основные переменные свободные, следовательно,

х₁ = х₂ = х₃ = х₄ = 0.

Значения базисных переменных приведены в ячейках В5:В7, следовательно,

у₁ = 16; у₂ = 110; у₃ = 100.

Действительно, если х₁ = х₂ = х₃ = х₄ = 0, т. е. продукция не выпускается, то величина y неиспользованного ресурса будет равна всему имеющемуся ресурсу, и прибыль при этом, естественно, будет равна 0 (В4 = 0).

Как мы знаем, решения бывают допустимыми и оптимальными. Каждое решение имеет свой признак. Приведем (без доказательства, достаточно сложного) эти очень важные признаки, которые нам потребуются в дальнейшем.

Признак 1

Признак 1 определяет,является ли полученное решение допустимым. Согласно этому признаку решение является допустимым, если в столбце свободных членов В5:В7 (целевая функция не рассматривается) все величины неотрицательные.

Признак 2

Признак 2 определяет наличие оптимального решения, при этом возможны 2 варианта:

r Признак 2а

Целевая функция имеет минимальное значение в том случае, когда все элементы в строке целевой функции С4:F4 (свободный член не рассматривается) будут отрицательными. Следовательно, на рис. 3.1.7 приведено решение при минимизации целевой функции. Действительно, если ничего не выпускать, то

х₁ = х₂ = х₃ = х₄ = 0,

и при этом прибыль будет F = В4 = 0.

r Признак 2б

Целевая функция имеет максимальное значение в том случае, когда все элементы в строке целевой функции С4:F4 будут положительными.

Поскольку таблица на рис. 3.1.7 не удовлетворяет признаку максимизации целевой функции, что нам требуется найти в решаемой задаче, то приступим к ее решению с помощью симплекс-метода.

Как мы говорили, поиск оптимального решения заключается в переборе вершин ОДР. При этом переход от одной вершины к другой производится по достаточно сложному алгоритму симплекс-метода, который заключается в обмене переменных. Каждый переход от одной вершины к другой, который, как мы знаем, называется итерацией, состоит в том, что одна базисная переменная приравнивается к нулю, т. е. переходит в свободную, а одна свободная переменная переводится в базисную. На каждой итерации проверяют удовлетворение признаков допустимого и оптимального решений. Такая процедура продолжается до тех пор, пока не будут удовлетворены оба признака. Применительно к нашей задаче последняя симплекс-таблица, полученная после второй итерации, будет иметь вид, приведенный на рис. 3.1.8.

Рис. 3.1.8

Из этой таблицы видно, что в столбце свободных членов все элементы положительные, тогда по признаку 1 решение является допустимым. В строке целевой функции все элементы также положительные. Следовательно, согласно признаку 2б решение является оптимальным в смысле максимизации целевой функции. В этом случае оптимальным решением будут величины:

х₁*= 10, х₃*= 6 (которые являются базисными);

х₂*= х₄*= 0 (так как они свободные);

целевая функция F=1320.

Таков результат решения задачи. Но это еще не все. Симплекс-таблица является мощным средством для выполнения анализа.

Посмотрим, что еще можно узнать из симплекс-таблицы. На рис. 3.1.8 видно, что свободные переменные у₁ = у₃ = 0, а базисная переменная у₂ = 26. Это значит, что в оптимальном плане величины неиспользованных трудовых и финансовых ресурсов равны нулю. Следовательно, эти ресурсы используются полностью. Вместе с тем, величина неиспользованных ресурсов для сырья у₂ = 26, значит, имеются излишки сырья. Вот какие выводы можно сделать с помощью симплекс-таблицы.

И это тоже, оказывается, еще не все. Но об этом чуть позже.

Методы анализа задач

3.2.1. Если решения нет

При решении задачи линейного программирования достаточно часто оптимального решения получить не удается. Это происходит по двум следующим причинам.

Причину 1 проиллюстрируем на следующем примере. Систему

(3.2.1)

представим графически (рис. 3.2.1). На рисунке видно, что нет таких значений х₁ и х₂, которые удовлетворяли бы системе (3.2.1). Значит, в данном примере ОДР отсутствует.

Про такую систему говорят, что ограничения несовместны. К сожалению, это очень часто встречается на практике, а не только теоретически возможный вариант. В таких случаях Excel будет выдавать сообщение Поиск не может найти подходящего решения.В общем случае несовместность может быть следствием двух причин:

rнеправильная математическая модель;

rнеправильные исходные данные.

Способы преодоления несовместности мы рассмотрим после того, когда научимся решать задачи линейного программирования в Excel.

Причину 2 рассмотрим на следующем примере. Построим систему

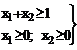(3.2.2)

Эта система показана на рис. 3.2.2, из которого видно — ОДР не ограничена сверху.

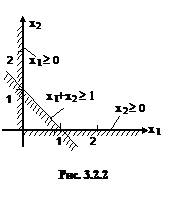
В таком случае при максимизации целевой функции

F = x₁ ® mах

решение получено быть не может, т. к. целевая функция, как и ОДР, не ограничена сверху. Если в задаче ОДР не ограничена, то Excel будет выдавать сообщение Значения целевой ячейки не сходятся.

 

Неограниченность целевой функции — это следствие ошибки в математической модели. Чтобы избежать таких ошибок, надо выполнять следующие правила:

1. При максимизации целевой функции она должна быть ограничена сверху либо с помощью ограничений, либо с помощью граничных условий, при этом модель с точки зрения содержания должна иметь вид:

(3.2.3)

2. При минимизации целевой функции она, соответственно, должна быть ограничена снизу, как это показано в (3.2.4).

(3.2.4)

3.2.2. Двойственность в задачах
линейного программирования

Еще немного теории. Рассмотрим теперь понятие о двойственности.

Каждой задаче линейного программирования, которую будем называть исходной, соответствует двойственная задача. Правила записи двойственной задачи рассмотрим на таком примере. Пусть имеется исходная задача

(3.2.5)

Двойственная задача формулируется по следующим правилам:

1. Каждому i-му ограничению исходной задачи соответствует переменная двойственной задачи, которую будем называть двойственной переменной и обозначать z_i. В системе (3.2.5) ограничению (а) соответствует переменная z₁, ограничению (б) — переменная z₂.

2. Каждой переменной исходной задачи соответствует ограничение двойственной задачи. В системе (3.2.5) три переменных х₁, х₂, х₃. Значит, двойственная задача должна иметь три ограничения.

3. Матрица коэффициентов при двойственных переменных в ограничениях двойственной задачи является транспонированной матрицей коэффициентов при переменных в ограничениях исходной задачи (3.2.5).

Матрица коэффициентов исходной задачи

.

Следовательно, транспонированная матрица

.

4. Если в исходной задаче ограничения имеют знаки неравенств Ј, то в двойственной они будут і.

5. Правые части ограничений в двойственной задаче равны коэффициентам при переменных в целевой функции исходной задачи.

6. Коэффициенты при двойственных переменных в целевой функции двойственной задачи равны правым частям ограничений исходной задачи.

7. Максимизация целевой функции исходной задачи заменяется минимизацией целевой функции двойственной задачи.

Таким образом, для исходной задачи (3.2.5) можно записать двойственную задачу

(3.2.6)

В общем виде исходной задаче

(3.2.7)

соответствует двойственная

(3.2.8)

Важное свойство двойственной задачи заключается в том, что

махF = minF_д.

При этом .

Если последнюю формулу записать для наглядности в форме

,

то видно, что двойственная переменная z _i является коэффициентом при b_i и, следовательно, показывает, как изменится целевая функция при изменении ресурса b_i на единицу. В литературе по оптимизации двойственные переменные принято называть двойственными оценками. В отчетах Excel двойственная оценка называется теневой ценой.

Очень существенно, что для нахождения двойственных оценок двойственную задачу решать не требуется. Их значения уже находятся в симплекс-таблице оптимального решения исходной задачи, приведенной для рассматриваемого примера на рис. 3.1.8.

Определить значение двойственных оценок можно следующим образом. Если некоторый i-ый ресурс используется не полностью, т. е. имеется резерв, значит, дополнительная переменная в ограничении для данного ресурса будет больше нуля. В нашем примере таким ресурсом является сырье, поскольку b₂ = 110 и его резерв y₂ = 26. Совершенно очевидно, что если бы сырья было не 110 единиц, а 111, то резерв стал бы равен не 26, а 27. При этом не произошло бы увеличения целевой функции. Следовательно, для второго ограничения двойственная переменная z₂ = 0. Таким образом, если по данному ресурсу есть резерв, то дополнительная переменная будет больше нуля, а двойственная оценка этого ограничения равна нулю.

В рассматриваемом примере трудовые ресурсы и финансы использовались полностью, поэтому их дополнительные переменные равны нулю. В таблице на рис. 3.1.8 переменные у₁ и у₃ являются свободными, значит у₁ = у₃ = 0. Если ресурс используется полностью, то его увеличение или уменьшение повлияет на объем выпускаемой продукции и, следовательно, на величину целевой функции.

Значение двойственной оценки при этом находится в симплекс-таблице (рис. 3.1.8) на пересечении строки целевой функции со столбцом данной дополнительной переменной. Для трудовых ресурсов при у₁ = 0 двойственная оценка z_i = 20, а для финансов при у₃ = 0 двойственная оценка z₃ = 10.

Результаты решения задачи, приведенные на рис. 3.1.8, сведены в таблицу, показанную на рис. 3.2.3.

Из этой таблицы видно, что при увеличении (уменьшении) трудовых ресурсов на единицу, целевая функция увеличится (уменьшится) на 20 единиц и будет равна

 

при увеличении F = 1320 + 20 ´ 1 = 1340,

при уменьшении F = 1320 - 20 ´ 1 = 1300.

Аналогично обстоит дело и с финансами. При увеличении (уменьшении) финансов на единицу целевая функция будет равна

при увеличении F = 1320 + 10 ´ 1 = 1330,

при уменьшении F = 1320 - 10 ´ 1 = 1310.

У внимательного читателя может возникнуть вопрос: а если ресурсы увеличить (уменьшить) на 5, 10, 15,...,100... Иными словами, в каких пределах справедливы эти зависимости?

Запомните вопрос и ждите ответа.

А мы пойдем дальше и для рассмотренной задачи распределения ресурсов (3.1.8) по приведенным выше правилам составим двойственную задачу

(3.2.9)

По аналогии с вводом дополнительных переменных у_i (3.1.9) введем дополнительные двойственные переменные v_j.

(3.2.10)

Значения дополнительных двойственных переменных специально вычислять не надо. Их значения уже определены в симплекс-таблице, приведенной на рис. 3.1.8. Фрагмент этой таблицы с обозначениями основных и дополнительных двойственных переменных показан на рис. 3.2.4, а их значения — на рис. 3.2.5.

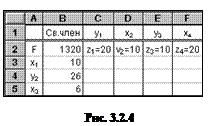
Рис. 3.2.5

Каков же смысл дополнительных двойственных переменных?

Если основные переменные (в нашем примере х₁ = 10, х₃ = 6) вошли в оптимальное решение, то их дополнительные переменные равны нулю (v₁ = 0, v₃ = 0). Если основные переменные не вошли в оптимальное решение, т. е. равны нулю (в примере
х₂ = х₄ = 0), то соответствующие им дополнительные переменные имеют положительное значение (v₂ = 10, v₄ = 20). Эти величины показывают, насколько уменьшится целевая функция при принудительном выпуске единицы данной продукции. Следовательно, если мы захотим принудительно выпустить единицу продукции Прод3, то целевая функция F уменьшится на 10 единиц и будет равна 1320 -10 ´ 1 = 1310.

И тот же вопрос: в каких пределах это справедливо? И тот же ответ: ждите ответа.

В заключение отметим, что в отчетах Excel дополнительная двойственная переменная называется редуцированная стоимость.

Из приведенного очевидно, что двойственные и дополнительные двойственные переменные являются мощным средством анализа полученного оптимального решения.

3.2.3. Анализ оптимального решения

Жизнь, как правило, не стоит на месте. Как говорится, все течет, все изменяется. В том числе и исходные данные, для которых находилось оптимальное решение. Изменится ли при этом полученное оптимальное решение? Чтобы ответить на этот вопрос, обратимся к нашей модели (3.1.8). Посмотрим, как влияет на оптимальное решение изменение двух элементов математической модели:

с_j — прибыли, получаемой при продаже единицы продукции x_j;

b_i — количества располагаемого ресурса.

Анализ влияния изменения c_j

В математической модели (3.1.8) целевая функция равна

F = 60x₁+70x₂+120x₃+130x₄®max.

Допустим, прибыль от продажи Прод1 с₁ = 60 изменится на величину Dс₁ и станет

с₁ = 60 + Dс_1. (3.2.11)

При этом строка целевой функции в исходной симплекс-таблице (рис. 3.1.7) примет такой вид, как на рис. 3.2.6.

В результате поиска оптимального решения фраг­мент последней симплекс-таблицы будет иметь вид, представленный на рис. 3.2.7. Отсюда можно сделать вывод, что к величинам, находящимся в таблице рис. 3.1.8, добавляются величины в строке x_j (ячейки B3:F3), умноженные на Dс₁.

Рис. 3.2.7

Согласно признаку 2а, сформулированному в 3.1.3, при максимизации целевой функции решение будет оптимальным в том случае, когда в строке целевой функции все элементы, кроме свободного члена, будут неотрицательны.

Значит, решение будет оптимальным при условии

(3.2.12)

Преобразуя (3.2.12), запишем:

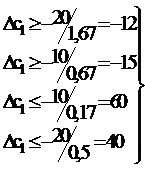
и окончательно

-12 £ Dс₁ £ 40.

Условие (3.2.12) определяет пределы изменения Dс₁ при которых сохраняется структура оптимального плана, т. е. будет выгодно по-прежнему выпускать продукцию х₁.

В отчетах Excel нижний предел (в примере равный 12) называется допустимое уменьшение; верхний предел, равный 40, — допустимое увеличение.

Если от пределов приращений Dc₁ перейти к пределам значения величины с₁, то можно записать

(3.2.13)

Таким образом, при изменении с₁ в пределах

minc₁ £ c₁ £ maxc₁ (3.2.14)

48 £ с₁ £ 100

будет по-прежнему выгодно выпускать продукцию х₁. При этом значение целевой функции будет

F = 1320 +10Dc_1.

Если выполнить аналогичные преобразования с с₂, с₃, с₄, то
получим

(3.2.15)

И далее по зависимостям, аналогичным (3.2.13), не трудно перейти к пределам значений с₂, с₃, с₄.

Анализ влияния изменения b_i

Рассмотрим влияние изменения ресурсов на примере изменения имеющегося количества сырья. При изменении трудовых ресурсов на Db₁ ограничение для них будет иметь вид:

x₁+x₂+x₃+x₄ £ 16Db₁,

что запишем в виде

y₁ = (16+Db₁) - (x₁+x₂+x₃+x₄).

При этом столбец свободных членов в симплекс-таблице будет иметь вид, показанный на рис. 3.2.8, а фрагмент симплекс-таблицы с оптимальным решением ¾ на рис. 3.2.9, из которого видно правило формирования свободных членов, аналогичное правилу формирования строки целевой функции.

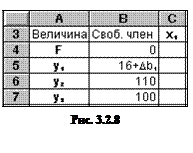
Рис. 3.2.9

В соответствии с признаком 1 решение будет допустимым в том случае, если все элементы в столбце свободных членов будут неотрицательными. Значит, из рис. 3.2.9 следует

откуда

Тогда для сохранения структуры оптимального плана изменение трудовых ресурсов должно быть в пределах

- 6 £ Db₁ £ 3,55.

Аналогично можно получить значения для Db₂, Db₃ и записать

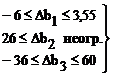(3.2.16)

Переход от Db_i к пределам b_i производится по зависимостям

(3.2.17)

и в результате получим

minb₁ = 16 - 6 = 10

maxb₁ = 16 +3,55 = 19,55

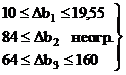(3.2.18)

Найденные пределы показывают границы, в которых могут изменяться ресурсы, чтобы структура оптимального решения, т. е. номенклатура выпускаемой продукции, остались без изменений. А это означает, что при изменении трудовых ресурсов в найденных пределах оптимальным, т. е. обеспечивающим наибольшую прибыль, является выпуск той же продукции х₁ и х_3, но в других количествах. При этом необходимо будет выпускать

х₁ = 10 + 1,67Db_1,

x₃ = 6 - 0,67Db_1.

При этом целевая функция будет

F = 1320 + 20Db_1.

Аналогично полученные зависимости для финансов будут иметь вид:

Поясним эти зависимости на следующем примере. Пусть увеличение финансов составляет

Db₃ = 10.

При этом получим

х₁ = 10 - 0,17 ´ 10 = 8,3,

х₃ = 6 + 0,17 ´ 10 = 7,7.

В данном случае целевая функция будет

F = 1320 +10 ´ 10 = 1420.

Видимо, было трудно представить, что при увеличении финансов для обеспечения максимизации прибыли выпуск продукции х₁ целесообразно уменьшить, а выпуск продукции х₃ — увеличить. Такое решение объясняется следующим. Как видно из условий задачи (рис. 3.1.6), прибыль с единицы продукции с₃ = 120, т. е. единица продукции Прод3 в 120/60 = 2 раза дает большую прибыль по сравнению с единицей продукции вида Прод1. В связи с этим оказалось целесообразным такое перераспределение выпуска продукции.

Мы полагаем, что приведенных примеров достаточно, чтобы показать, на какие важные вопросы можно получить ответы с помощью математической модели. Следует подчеркнуть, что все эти ответы могут быть получены без дополнительного решения задачи, а только используя симплекс-таблицу основной задачи (рис. 3.1.8).

И еще один важный вопрос. Говоря о двойственных и дополнительных двойственных переменных, мы оставили без ответа поставленные вопросы о пределах, в которых справедливы полученные значения этих переменных. Пришла пора дать ответ на эти вопросы. Оказывается, что пределы изменения Db_i — это и есть пределы справедливости двойственных оценок z_i. А пределы изменения Dc_j — это пределы справедливости дополнительных двойственных оценок v_j.

На этом мы заканчиваем рассмотрение тех некоторых теоретических положений, без знания которых было бы не ясно, откуда в отчетах Excel появляются соответствующие представляемые величины.

Читатель, который не поленился внимательно разобраться в симплекс-методе и анализе оптимальных решений, надеемся, согласится с известным положением, что нет ничего практичнее хорошей теории.

3.2.4. Вариантный анализ

Для задач распределения ресурсов наибольший интерес представляет решение двух задач вариантного анализа:

rпараметрического анализа, в ходе которого решаются задачи при различных значениях одного из параметров;

rпоиска решений по нескольким целевым функциям.

При решении задач распределения ресурсов по нескольким целевым функциям возможна одна из двух постановок задачи: при заданных ресурсах максимизировать получаемый результат; либо при заданном результате минимизировать используемые ресурсы.

Если обозначить Q — ресурсы, R — результат их применения, то при заданных зависимостях результата R = f₁(x_j) и требуемых ресурсов Q = f₂(x_j) от количества выпускаемой продукции эти постановки могут быть записаны так:

Первая постановка

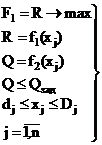(3.2.19)

Вторая постановка

(3.2.20)

Решение задачи распределения ресурсов в этих двух постановках рассмотрим на примере задачи, приведенной на рис. 3.2.10.

Рис. 3.2.10

Этот пример отличается от рассмотренного ранее (рис. 3.1.6) введением граничных условий на переменные и изменением некоторых норм расхода. Для отличия от предыдущей задачи здесь присвоены имена Вид1, Вид2, Вид3, Вид4 типам выпускаемой продукции. В решаемой задаче ограничения и граничные условия имеют вид:

(3.2.21)

Будем решать эту задачу в двух приведенных выше постановках.

В первой постановке — максимизация результата — целевая функция будет иметь вид:

F₁ = 60x₁+70x₂+120x₃+130x₄ ® max (3.2.22)

Для решения задачи во второй постановке — минимизация используемых ресурсов — введем в (3.2.21) дополнительные переменные у₁, у₂, у_3.

(3.2.23)

Переменные у₁, у₂, у₃ показывают величину неиспользованного ресурса. Значит, если мы хотим минимизировать используемый ресурс, то нужно максимизировать неиспользованный ресурс, тогда во второй постановке целевая функция будет

F₂ = y₁+ y₂ + y₃ ®max. (3.2.24)

В этой постановке, как и при любой минимизации, должен быть задан минимально допустимый результат. В качестве такого заданного результата принимаем нижние значения граничных условий для переменных, приведенные на рис. 3.2.10 и в (3.2.21).

Решение этих задач проведем в разделе 3.4.3 после ознакомления с поиском оптимальных решений в Excel.

3.3. Решение задач линейного
программирования с помощью Excel

3.3.1. Блок-схема решения задачи

Последовательность необходимых работ, выполняемых при решении задач линейного программирования с помощью Excel, приведена на блок-схеме (рис. 3.3.1).

Рис. 3.3.1

Подробное описание этих работ и составляет содержание данной главы.

3.3.2. Ввод условий задачи

Ввод условий задачи состоит из следующих основных шагов:

1. Создание формы для ввода условий задачи.

2. Ввод исходных данных.

3. Ввод зависимостей из математической модели.

4. Назначение целевой функции.

5. Ввод ограничений и граничных условий.

Последовательность работ рассмотрим на примере задачи распределения ресурсов, исходные данные которой приведены на рис. 3.1.6, а математическая модель имеет вид (3.1.8).

Алгоритм 3.3.1. Ввод данных для решения задачи
линейного программирования

1. Для задачи, приведенной на рис. 3.1.6, сделать форму для ввода условий задачи (рис. 3.3.2).

Рис. 3.3.2

Весь текст на рис. 3.3.2 (и в дальнейшем) является комментарием и на решение задачи не влияет.

2. Ввести исходные данные в форму (рис. 3.3.2).

 

Необходимые исходные данные приведены на рис. 3.1.6.

Переход от рис. 3.1.6 к рис. 3.3.2 показан на рис. 3.3.3.

3. Ввести зависимости из математической модели (3.1.8).

Для наглядности (но не обязательно!) можно перейти к режиму представления формул (алг. 2.1.12). При этом ввод данных приводится на рис. 3.3.4, а режим представления формул ¾ на рис 3.3.5.

Рис. 3.3.4

Рис. 3.3.5

3.1. Ввести зависимость для целевой функции:

Ø Курсор в F6.

Ø Курсор на кнопку Мастер функций.

Ø М1.

На экране: диалоговое окно Мастер функций шаг 1 из 2.

Ø Курсор в окно Категорияна категорию Математические.

Ø М1 .

Ø Курсор в окноФункции на СУММПРОИЗВ.

Ø M1.

Ø Далее .

На экране: диалоговое окно (рис. 3.3.6).

Рис. 3.3.6

Ø В массив 1 вв