Географические координаты.
Так же, как и каждый дом имеет свой адрес (с названием улицы, города), также и каждое место на поверхности Земли можно записать в виде адреса, используя линию широты (параллель) и линию долготы (меридиан), проходящие через это место. Чтобы найти некоторый объект в городе, в большинстве случаев достаточно знать его адрес. Трудности возникают, если нужно объяснить, где находится, например, дачный участок, место в лесу. Универсальным средством указания местоположения служат географические координаты.
При попадании в аварийную ситуацию, человек первым делом должен уметь ориентироваться на местности. Иногда необходимо определить географические координаты своего местоположения, например, чтобы передать спасательной службе или для других целей.
В современной навигации стандартно используется всемирная система координат WGS-84. В этой системе координат работают все GPS навигаторы и основные картографические проекты в Интернете. Координаты в системе WGS-84 столь же общеупотребимы и понятны всем, как всемирное время.
Местоположение любого объекта на поверхности Земли, его «адрес», определяется географической широтой («адрес» по горизонтали) и географической долготой («адрес» по вертикали). Широта и долгота — это географические координаты точки земной поверхности
Географическая широта. Параллели — это линии широты. Для всех точек одной и той же параллели широта одинакова. Начало отсчета широт — экватор, все точки которого имеют нулевую широту. От экватора широта отсчитывается в градусах вдоль меридиана до заданной точки. Все точки земной поверхности, находящиеся к северу от экватора, имеют северную широту (с. ш.); широта точек к югу от экватора — южная (ю. ш.). Следовательно, широта показывает, насколько далеко к северу или к югу от экватора расположен заданный пункт. Как северная, так и южная широта отсчитываются от 0 до 90° (см.приложение 1,рис.7)
|
|
Географическая широта заданной точки определяется величиной в градусах дуги меридиана от экватора до параллели, проходящей у точку.
Географическая долгота. Долгота отсчитывается в градусах вдоль параллели. Началом отсчета долгот условно выбран Гринвичский (нулевой, начальный) меридиан, который проходит через старую Гринвичскую обсерваторию в Лондоне. Начальный меридиан и меридиан 180° разделяют Землю на Восточное и Западное полушария. Все точки Восточного полушария имеют восточную долготу (в. д.), а Западного — западную долготу (з. д.). Как восточная, так и западная долгота отсчитываются от 0 до 180°. Цифры, обозначающие градусы долготы, написаны на глобусе и на карте полушарий у точек пересечения меридианов с экватором. Географическая долгота заданной точки определяется величиной в градусах дуги параллели от начального меридиана до меридиана, проходящего через эту точку. (см.приложение 1,рис.8)
Построение изображений созвездий на координатной плоскости.
У древних греков существовала легенда о созвездиях Большой Медведицы и Малой Медведицы:«Всемогущий бог Зевс решил взять себе в жены прекрасную нимфу Калисто, одну из служанок богини Афродиты, вопреки желанию последней. Чтобы избавить Калисто от преследований богини, Зевс обратил Калисто в Большую Медведицу, а ее любимую собаку – в Малую Медведицу и взял их на небо». Существует множество легенд и мифов о созвездиях. Фантазия древних греков поместила их на небо. Так появились созвездия Цефея, Андромеды, Персея и т.д. Знакомство с координатной плоскостью и вид звездного неба натолкнули на мысль, о переносе некоторых созвездий на координатную плоскость.
|
|
Созвездие Лев. В этом созвездии запечатлен Немейский Лев, над которым одержал победу Геракл.
Созвездие Близнецы. Созвездие названо в честь двух неразлучных братьев, сыновей Елены Прекрасной – Кастора и Полидевка..
Большая Медведица. Согласно греческому мифу это созвездие олицетворяет прекрасную нимфу Каллисто, превращенную Зевсом в Медведицу, чтобы спасти её от мести Геры.
Малая Медведица. Созвездие известно как Малый Ковш, последняя звезда в "ручке" которого – Полярная.
Орион. В греческой мифологии Орион – сын Посейдона и Эвриалы, великий охотник.
Телец. Созвездие названо в честь быка, на котором Европа переплыла море и попала к Зевсу на Крит. (см.приложение 2,рис.1)
Создание «рисунков» в прямоугольной системе координат.
На координатной плоскости интересно строить рисунки, используя построение графов по координатам. Нужно сначала нарисовать рисунок, а затем его перенести на координатную плоскость, но при этом плавные соединения должны быть в виде отрезков.
(см.приложение 2,рис.2)
Приложение 1
Рис.1 Рене Декарт
Рис.2 Координатная плоскость
Рис.3
Рис.4
Рис.5
Рис.6
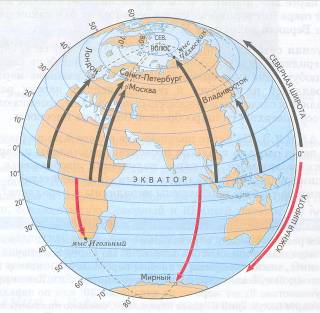Рис.7
|
|
Рис.8
Приложение 2
Рис.1
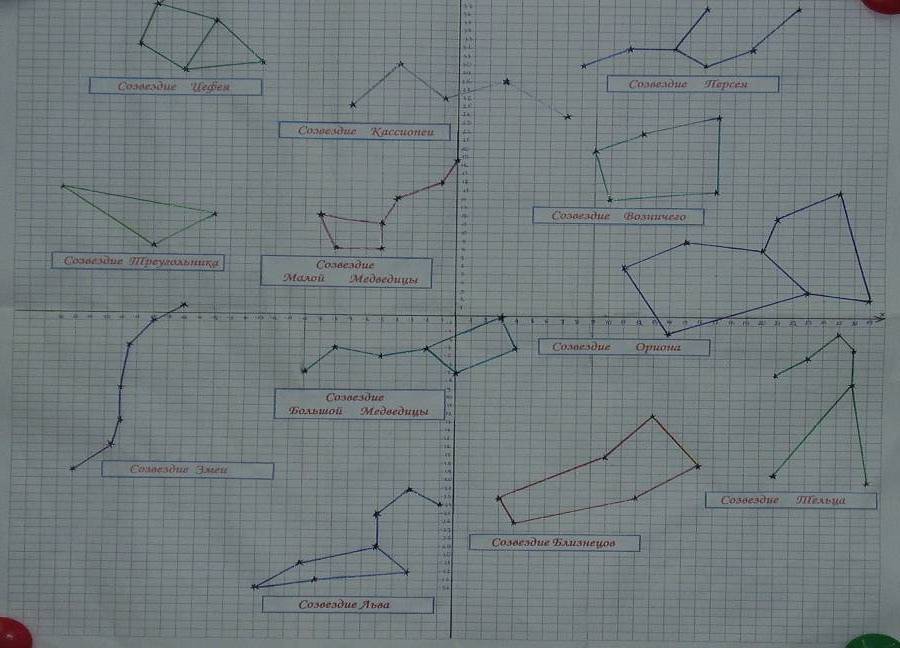
Рис.2
«Жираф»
(1;11) (9;-12) (-6;1)
(3;12) (10;-13) (-8;-5)
(8;13) (10;-14) (-9;-10)
(13;11) (9;-14) (-9;-12)
(16;-8) (9;-15) (-10;-13)
(17;6) (8;-15) (-9;-14)
(17;4) (7;-14) (-10;-15)
(15;2) (7;-13) (-11;-14)
(18;0) (6;-13) (-12;-15)
(15;0) (3;-7) (-13;-14)
(16;-3) (3;-5) (-12;-12)
(15;-5) (1;-1) (-11;-12)
(15;-7) (-2;-1) (-11;-10)
(14;-9) (-3;-4) (-10;-7)
(12;-11) (0;-13) (-10;-4)
(12;-12) (0;-14) (-9;0)
(10;-12) (-1;-13) (-10;6)
(8;-10) (-2;-14) (-8;9)
(7;-8) (-3;-14) (-6;11)
(9;-5) (-4;-13) (-7;12)
(10;-2) (-3;-12) (-12;10)
(10;-1) (-3;-10) (-8;14)
(7;-1) (-4;-7) (-5;13)
(12;2) (-6;-15) (-3;13)
(14;5) (-5;-16) (1;11)
(12;8) (-6;-17)
(9;9) (-7;-16) Глаза:
(4;6) (-7;-17) (11;-2)
(4;3) (-8;-16) (13;-2)
(3;0) (-8;-15)
(4;-1) (-7;-14) Нос:
(5;-5) (-8;-13) (10;-10)
(8;-12) (-5;-3) (11;-10)
«Слонёнок»
(2;4) (10;-5) (7;1) (11,5;-1)
(2;1) (10;-9) (5;1) (10,5;-3,5)
(3;0) (12;-9) (4;0) (9;-4)
(4;1) (12;-3) (3;1) (7;-3)
(3;-1) (13;-7) (3;4) (7;-1)
(5;-3) (13;-3) (2;4) Глаза:
(6;-3) (12;1,5) Ухо: (5;0)
(6;-9) (10;-1) (7;1) (6;0,5)
(8;-9) (8;-1) (9;1,5) (7;0)
(8;-5) (8;0) (11;0,5) (6;-0,5)
«Кит»
(0;9) (-2;-8) (7;-10) (12;-9)
(-1;-11) (0;-7) (-1;-10) (10;-10)
(-3;13) (1;-6) (-3;-8) (9;-9)
(-4;12) (3;-5) (-1;-9,5) (10;-7)
(-2;8) (5;-6) (0;-8) (9;-3)
(-2;5) (7;-7) (1;-10) (4;2)
(-4;3) (9;-9) (2;-7) (4;2)
(-5;1) (3;-6) (3;-10) (1;7)
(-5;-5) (1;-7) (4;-7) (4;12)
(-4;-7) (-1;-7) (5;-10) (3;13)
(-3;-8) (-3;-8) (6;-8) (1;11)
(-5;-8) (-2;-10) (7;-10) (0;9)
(-6;-10) (0;-11) (7;-9) Точка:
(-4;-9) (6;-11) (9;-9) (-2;-7)
(-3;-8) (9;-9) (10;-8) (8;-7)
«Лось»
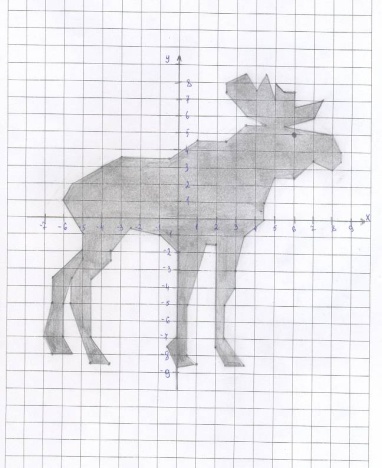(-5,5;2) (-4;3) (-3;3,5) (-0,5;3,5)
(1;4,5) (2,5;4,5) (3,5;5,5) (4,5;5,5)
(3,5;6) (2,5;7,5) (2,5;8) (3,5;8,5)
(4;7,5) (4,5;8,5) (5;7) (5;8)
(5,5;7,5) (6;7,5) (6;6,5) (7,5;7)
(7;6) (5,5;5,5) (8;5) (8,5;4)
(8,5;3,5) (8;3) (7;3,5) (6;2,5)
(5;2,5) (4,5;1) (4,5;0) (3,5;-1)
(3;-3) (3;-4) (2,5;-5) (2,5;-7)
(3,5;-8,5) (2,5;-8,5) (2;-7,5) (2;-1,5)
(1,5;-1,5) (0,5;-5) (0,5;-8)
(1;-8,5) (0;-8,5) (-0,5;-7,5) (0;-7)
(0;-2) (-1;-1) (-2,5;--0,5) (-3,5;-2)
(-3,5;-2,5) (-4,5;-3,5) (-4,5;-7) (-3,5;-8,5)
(-4,5;-8,5) (-5,5;-5) (-5,5;-3,5)
(-5;--2,5) (-5;--1) (-6;1)
(-5,5;2) и
(-5;-2) (-6,5;-3,5) (-6,5;-5) (-7;-7)
(-6,5;-8) (-5,5;-8) (-6;-7) (-6;-5)
(-5,5;-3,5) и
(6;5)
«Крокодил»
(15;2) (-5;-3) (7;-4)
(15;3) (-6;-4) (6;-3)
(10;1) (-3;-4) (8;-4)
(9;2) (-2;-3) (10;-4)
(8;2) (-1;-4) (8;-3)
(7;1) (1;-4) (15;0)
(3;1) (0;-3) (10;0)
(-4;0) (4;-3) Глаз:
(-16;-2) (4;-4) (9;1)
Карточка № 1
Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
(3;3); (0;3); (-3;2); (-5;2); (-7;4); (-8;3); (-7;1); (-8;-1);
(-7;-2); (-5;0); (-1;-2); (0;-4); (2;-4); (3;-2); (5;-2); (7;0); (5;2);
(3;3); (2;4); (-3;4); (-4;2); глаз (5;0).
Карточка № 2
Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
(3;0); (1;2); (-1;2); (3;5); (1;7); (-3;6); (-5;7); (-3;4);
(-6;3); (-3;3); (-5;2); (-5;-2); (-2;-3); (-4;-4); (1;-4); (3;-3);
(6;1); (3;0); глаз (-1;5).
Карточка № 3
Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
(1;7); (0;10); (-1;11); (-2;10); (0;7); (-2;5); (-7;3); (-8;0);
(-9;1); (-9;0); (-7;-2); (-2;-2); (-3;-1); (-4;-1); (-1;3); (0;-2);
(1;-2); (0;0); (0;3); (1;4); (2;4); (3;5); (2;6); (1;9); (0;10); глаз (1;6).
Карточка № 4
Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
(1;-4); (1;-6); (-4;-6); (-3;-5); (-1;-5); (-3;-4); (-3;-3);
(-1;-1); (-1;0); (-3;0); (-3;-1); (-4;-1); (-4;0); (-3;1); (-1;1);
(-1;2); (-3;3); (-1;4); (0;6); (1;4); (1;2); (3;4); (6;5); (9;2); (9;0);
(9;-4); (6;-4); (5;-1); (4;-1); (1;-4); глаз (-1;3).
Ответы: 2 – утенок; 3 – заяц; 4 – белка; 5 – кошка.
