В нашей задаче имеется только 4уровня в иерархической модели сети связи. Для решения задачи используем следующий графический метод. Оптимизация проводится дважды: сначала минимизируется линия связи по координате X, а затем таким же образом по координате Y.
Введем понятие удельной стоимости сети связи:
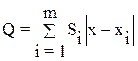
Здесь x - искомая оптимальная координата объекта X, который соединен с объектами Xi координаты xi которых известны. Si - удельная стоимость линии связи от объекта X к объекту Xi. m - число объектов связанных с объектом X.
Удельная стоимость сети связи не является стоимостью как таковой, она только характеризует стоимость сети связи в зависимости от положения объектов.
Удельная стоимость записывается для каждой координаты, уровня и фрагмента отдельно. При этом верхний индекс при Q указывает на координату, первый нижний индекс на уровень, а второй нижний индекс на фрагмент (или объект).
Вначале, составляется выражение Q для 0-го уровня, что в общем виде можно записать как:
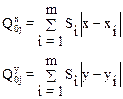
Здесь j - номер фрагмента.
В этом случае Q будет характеризовать стоимость сети связи между объектами 0-го уровня и объектами 1-го уровня. j - номер объекта на первом уровне, который связан с объектами уровня 0.
Рассмотрим координату Х:
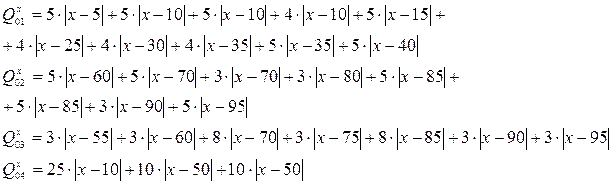
Для минимизации стоимости сети связи необходимо решить задачу:
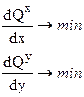
Так как в выражении для Q разность (x-xi) стоит под знаком модуля, то при определении производной необходимо следить чтобы эта разница всегда была больше 0, т.е. если значение производной определяется на промежутке где x>xi, то эта разность запишется как (x-xi), а если значение производной определяется на промежутке где x<xi, то эта разность запишется как (xi-x).
Разность (x-xi) назовем узловой точкой с координатой xi. Для каждой Q координатная ось X разбивается узловыми точками на ряд отрезков в каждом из которых производная имеет постоянное значение. Такая координатная ось изображается для всех Q 0-го уровня. На эту ось наносятся значения координат узловых точек и значения производной в образуемых отрезках.
Определим диапазон изменения производной. Примем, что x>"xi, тогда
 Пусть теперь x<"xi, тогда
Пусть теперь x<"xi, тогда
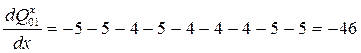
Т.е. диапазон изменения производной [-46; +46].
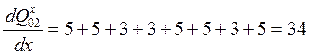
Пусть теперь x<"xi, тогда
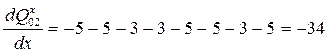
Т.е. диапазон изменения производной [-34; +34].
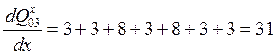
Пусть теперь x<"xi, тогда

Т.е. диапазон изменения производной [-31; +31].
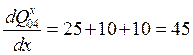
Пусть теперь x<"xi, тогда
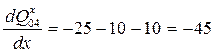
Т.е. диапазон изменения производной [-45; +45].
Удельная стоимость линии связи от УСД к ЭВМ (магистраль связи) накладывает ограничение на область поиска оптимальных координат. Эта удельная стоимость приводится в П1 таблица 4. Она зависит от типа выбранного интерфейса. В нашем случае она равна 10. Поэтому область поиска оптимальных координат уменьшается до диапазона изменения производной [-10; +10].
Построим график производной. Для этого нужно найти всего по одному значению производной в каждом из отрезков, образуемых узловыми точками
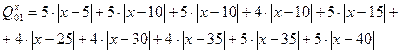

Область поиска координаты X для УСД1 равна (10; 30).
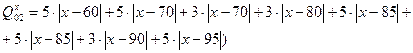

Область поиска координаты X для УСД2 равна (70;85).
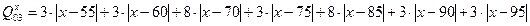
 Область поиска координаты X для УСД3 равна (70; 85).
Область поиска координаты X для УСД3 равна (70; 85).
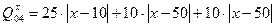

Область поиска координаты X для ЭВМ равна (10; 50).
Приведем диаграмму координатных осей для Q01x, Q02x, Q03x,Q04x.

рис.17
В первую очередь определяется координата единственного объекта на самом нижнем уровне иерархии. В качестве значения координаты выбирается любое значение из отрезка, где производная ближе всего к 0 (чаще это концевые точки такого отрезка): x21=50.
Остальные координаты (всех объектов уровня 1) определяются по правилу:
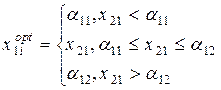
Где a11 и a12 - оконечные точки области поиска оптимальных координат для соответствующих Q1i.
Определим оптимальные координаты для УСД1, УСД2, УСД3,УСД4 и ЭВМ:
УСД1
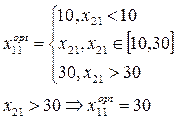
УСД2

УСД3

ЭВМ

Рассмотрим координату У:
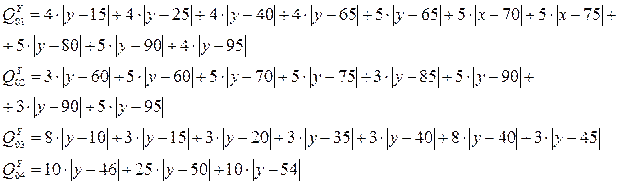
Определим диапазон изменения производной. Примем, что у>"уi, тогда
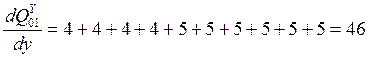 Пусть теперь x<"xi, тогда
Пусть теперь x<"xi, тогда
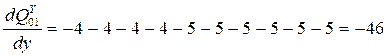
Т.е. диапазон изменения производной [-46; +46].
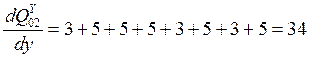
Пусть теперь x<"xi, тогда
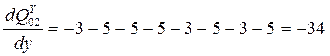
Т.е. диапазон изменения производной [-34; +34].
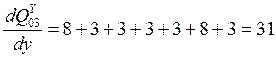
Пусть теперь x<"xi, тогда
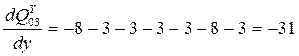
Т.е. диапазон изменения производной [-31; +31].

Пусть теперь x<"xi, тогда
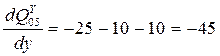
Т.е. диапазон изменения производной [-45; +45].
Построим графики производных.
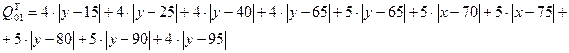

Область поиска координаты Y для УСД1 равна (65; 75).


Область поиска координаты Y для УСД2 равна (70; 90).
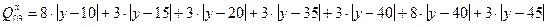

Область поиска координаты Y для УСД3 равна (15; 40).
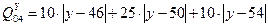

Область поиска координаты Y для ЭВМ равна (46; 54).
Приведем диаграмму координатных осей для Q01y, Q02y, Q03y,Q04y.

В первую очередь определяется координата единственного объекта на самом нижнем уровне иерархии. В качестве значения координаты выбирается любое значение из отрезка, где производная ближе всего к 0 (чаще это концевые точки такого отрезка). В нашем случае это будет координата разъема, примем ее равной: y21=55.
Остальные координаты (всех объектов уровня 1) определяются по правилу:
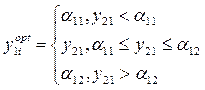
Где a11 и a12 - оконечные точки области поиска оптимальных координат для соответствующих Q1i.
Определим оптимальные координаты УСД1, УСД2, УСД3,УСД4 и ЭВМ:
УСД1

УСД2

УСД3
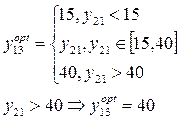
ЭВМ
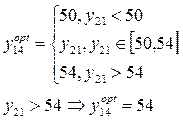
После того как найдены оптимальные координаты и по оси X и по оси Y для всех объектов АСНИ, данные о них сводятся в таблицу 11:
Таблица 11
| X | Y | |
| УСД1 | ||
| УСД2 | ||
| УСД3 | ||
| ЭВМ |
ЭТАП 4