В условиях современной технологии обогащения магнетитовых кварцитов естественный, ненамагниченный магнетит, содержащийся в сливе мельниц I стадии измельчения, попадает непосредственно в рабочие поля магнитных сепараторов напряженностью 80¸112 кА/м и флокуляция происходит лавинообразно (практически мгновенно), поэтому захват немагнитных зерен (кварца и др.) неизбежен [20].
Для того чтобы избежать этого в 1-ой условно принятой четверти было принято решение установить подающий лоток, расположенный в соответствии со следующими теоретическими соображениями. Величина напряженности магнитного поля в зависимости от расстояния находится в соответствие с формулой Сочнева [75]:
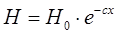, (4.4)
где Н, Н0 - величина напряженности магнитного поля,
с - коэффициент,
х - расстояние.
А захват частиц кварца напрямую зависит от скорости образования флокул, которая, в свою очередь, зависит от их размера, прямопропорционально зависящего от напряженности поля.
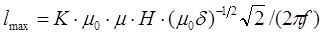, (4. 5)
где lmax - длина флокулы,
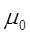- магнитная проницаемость вакуума,
- магнитная проницаемость среды,
Н - напряженность магнитного поля,
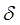- плотность пряди,- частота бегущего магнитного поля,
К - эмпирический коэффициент, зависящий от свойств пульпы, определяемый опытным путем.
При этом учитывалась как методика разработки и конструирования сепараторов, разработанная до этого и принятая на данный момент, так и методика, разработанная специалистами НТЦ МГГУ «Горнообогатительные модульные установки» для высокоселективных сепараторов типа ВСПБМ.
Механические силы, разрушающие флокулы, обеспечиваются турбулентным режимом и вибрацией. Кроме того, очень важно не допустить перепада напряженности поля в сторону снижения ее при подаче материала в рабочую зону сепаратора, так как при этом часть селективных флокул может разрушаться, а влияние агрегирования снижается.
Тогда равнодействующую силу для данного участка можно записать как:
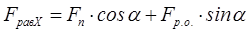, (4.6)
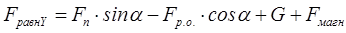, (4.7)
где FравнX и FравнY - соответственно равнодействующая сила относительно оси X и Y; α - угол наклона питателя, Fп - гидромеханическая сила, действующая на частицу, находящуюся на питающем лотке, Fр.о. - сила реакции опоры лотка, G - сила тяжести, Fмагн - магнитная сила
Рассматривая данные уравнения, заметим, что время нахождения частицы в зоне удерживания зависит от скорости подачи пульпы в питающее устройство, расстояния до магнитов, а также напряженности магнитного поля, создаваемого магнитной системой. Остальными взаимодействиями, такими как: вязкость среды, трение м/у различными частицами и т.п. можно пренебречь, т.к. их влияние значительно меньше, а также это значительно усложняет расчет. Также следует учесть, что рассматривая описанные уравнения, определяющим условием воздействия на частицу становится магнитная сила, т.к. скорость движения пульпы определяет лишь начало флокулообразования, а степень флокуляции суспензии, а значит и количество захваченных в объем флокулы частиц породы, зависит от расстояния до поверхности магнитов - поверхности барабана, соответственно. Таким образом, обеспечивая ламинарный заход исходного питания на поверхность барабана под углом, уменьшающим резкое возрастание размера флокулы, можно обеспечить невысокий захват частиц породы и сростков в объем флокулы, что в дальнейшем обеспечивает минимальное количество пустой породы, попадающей на барабан.
С использованием различных методик экспериментально изучалась зависимость степени флокуляции суспензии ψ от напряженности намагничивающего поля Не.
На участке I, который соответствует равновесной части процесса, степень флокуляции пропорциональна Rмех - равнодействующей магнитных и гидромеханических сил, действующих на флокулу.
В этой зоне FМ ≤ Rмех, что обусловливает равновесный характер процесса. Так как FМ пропорциональна H2, то Ψ1=kH2. При этом именно этот участок определяет захват частиц пустой породы, т.е. зависит от значения напряженности, находящейся в экспоненциальной зависимости от расстояния частицы до поверхности барабана, т.е.
Ψ1=k*(H0*ecx)2 (4.8)
Исходя из данного условия, а также из того, что на относительно малом расстоянии турбулентность, а значит и число Re, резко не изменяется, а угол, при котором происходит наиболее плавное изменение величины напряженности поля, соответствует углу, находимому из уравнения касательной к окружности [74], получаем:
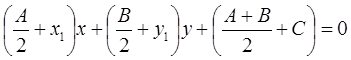, (4.9)
где А, В, С - коэффициенты окружности; x, y - координаты центра окружности; x1, y1 - координаты точки касания к окружности
Решая данное уравнение относительно окружности с центром в точке (0,0) и радиусом равным 450, а также, учитывая конструктивное расположение питающей камеры, можно определить искомый угол между касательной и горизонталью. Данный угол будет равняться 280,48´.
Таким образом, исходя из изложенного ранее, оптимальным углом подачи питания на барабан можно считать угол, равный 280,48´. Для проверки данного теоретического утверждения было принято решение о создании лабораторной модели, а также ее испытаний при режимах близких, либо соответствующих режимам работы промышленного сепаратора.