Логика высказываний. Нечёткие множества.

Отрицание высказывания A означает, что A не произойдёт и обозначается . Конъюнкция высказываний A и B означает, что произойдёт A и B и обозначается A B. Дизъюнкция высказываний A и B означает, что произойдёт A или B и обозначается A B. Строгая дизъюнкция высказываний A и B означает, что произойдёт или A,или B и обозначается A ∆ B.

Двухместная логическая операция, соответствующая обороту “ если…, то… ”, посредством которого образуются условные предложения, называется импликацией. Высказывание “ если A, то B ” записывается в виде .

Логический оператор □ выражает необходимость, а ◊ - возможность.

Для любого чёткого множества A и любого элемента x можно определить характеристическую функцию:

(3.1)

Например, если А – множество букв в слове “ глагол ” (А: ), то для любой буквы кириллицы легко найти характеристическую функцию. Так, 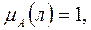так как буква “ л” входит в слово, а , так как буква “в” в него не входит.

Множество называется нечётким, если нельзя точно определить, принадлежат ли ему элементы. Нечёткость множества тесно связана с понятием лингвистической переменной (далее – ЛП), значениями которой являются слова или предложения. Например, во фразе “Миша вернётся около десяти часов вечера” ЛП “около десяти часов вечера” принимает значения из множества [21-30; 22-30]: неясно, когда именно вернётся Миша. Во фразе “Её жених – молод” ЛП “молод” принимает значения на огромном интервале [16; 40].

В случае нечёткого множества характеристическая функция, называемая функцией принадлежности, может принимать несколько значений, принадлежащих интервалу [0,1]. Носителем нечёткого множества Supp A называется множество элементов, для которых μ _A (x) > 0. Если при каком-то значении x μ _A (x) = 1, то множество называют нормальным, а если это – неверно, то – субнормальным.

Если максимальное значение μ _A (x) достигается в одной точке, то функция μ _A (x) называется унимодальной.

Операции конъюнкции и дизъюнкции для нечётких множеств определяется совсем иначе, чем для чётких множеств:

, (3.2) Операция отрицания нечёткого множества вводится аналогично вероятности отрицания высказывания (2.2):

(3.3)

Индексы референции, которыми могут быть снабжены личные, возвратные местоимения и одушевлённые подлежащие, маркируют актанта – участника ситуации. В случае нечёткого высказывания актант может быть определён несколькими способами, при этом индексы разделяются знаком /. Для отрицания используется знак *.

Пример 1.Даны следующие простые высказывания:

A₁ – “ Существительное относится к женскому роду ”,

A₂ – “ Существительное стоит в родительном падеже ”,

A₃ – “ Существительное стоит во множественном числе ”.

Описать события с помощью высказываний A_i, i =1,2,3:

a) B₁ – “ Существительное женского рода стоит в родительном падеже и во множественном числе ”.

b) B₂ – “ Существительное женского рода стоит в родительном падеже или во множественном числе ”.

c) B₃ – “ Существительное или относится к женскому роду, или стоит в родительном падеже, но не во множественном числе ”.

d) B₄ – “ Существительное не относится к женскому роду или стоит не в родительном падеже, но во множественном числе ”.

a) Все высказывания верны, поэтому: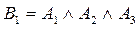

b) Верно первое высказывание, а также второе или третье:

c) Либо верно первое высказывание, либо второе и не третье, здесь строгая дизъюнкция:

d) Первое высказывание неверно либо второе неверно, а верно третье:

Пример 2.Дано сложное высказывание: “ Если пойдёт дождь, то останусь дома, а уж если останусь дома, дочитаю книгу, но телевизор не включу ”. Введём простые высказывания: A₁ – “ Пойдёт дождь”, A₂ – “ Останусь дома ”, A₃ – “ Дочитаю книгу ”, A₄ – “ Включу телевизор ”. Построить логическую схему предложения.

Из события A₁ вытекает высказывание A₂, а из него A₃ и не A₄. Поэтому логическая схема: .

Пример 3.Дано сложное высказывание: “ Если нужно написать отчёт, то займусь этим на выходных или, возможно, отложу на следующую неделю ”. Введём простые высказывания: A₁ - “ Написать отчёт”, A₂ - “ Займусь этим на выходных ”, A₃ - “ Отложу на следующую неделю”. Построить логическую схему предложения.

Из необходимости высказывания A₁ следует или высказывание A₂ или возможность высказывания A₃. Логическая схема: □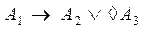

Пример 4. Слово содержит несколько букв. Найти функцию принадлежности числа букв слова. Построить дополнение множества. Проверить нормальность и унимодальность множеств, найти их носители.

В слове никак не может быть одна буква, а также более пяти букв. В остальных случаях функции принадлежности вычисляется как вероятность, вычисляемая каждым решающим задание субъективно. Определим универсальное множество как U = {1,2,…,8}. Запишем решение в виде таблицы:

x
		0,8	0,7	0,5	0,1

Supp A = {2, 3, 4, 5}. Множество является субнормальным, так как не содержит 1, и унимодальным, так как максимальное значение 0,8 соответствует одному значению x.

Теперь найдём функцию принадлежности для дополнения множества :

x
		0,2	0,3	0,5	0,9

Supp = U. Множество является нормальным, так как содержит 1, но не унимодальным, так как максимальное значение 1 соответствует нескольким x.

Пример 5. В шестисложной русской фразе есть несколько французских (множество A) и английских (множество B) заимствований, причём первых – больше. Найти функции принадлежности числа слов множеств A, B, .

Число английских заимствований не превосходит 3, иначе оно может оказаться больше числа французских заимствований. Поэтому для множеств A и B можно определить функции принадлежности так:

x
		0,8	0,7	0,6	0,3	0,1

x
		0,6	0,8

Некоторые слова могут быть заимствованиями из одного из двух языков – английского или французского, это приводит к дизъюнкции множеств (конъюнкция в данном случае невозможна). По формуле (3.2) вычисляем значение функции принадлежности для каждого из значений x:

Max (0; 0) = 0, max (0,8; 0,6) = 0,8, max (0,7; 0,8) = 0,8,

max (0,6; 0) = 0,6, max (0,3; 0) = 0,3, max (0,1; 0) = 0,1.

Теперь запишем эти результаты в виде таблицы:

x
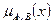
		0,8	0,8	0,6	0,3	0,1

Пример 6. Найти носитель нечёткого высказывания: “Она вряд ли успеет прочесть книгу”.

Носителем события является интервал, для которого функция принадлежности положительна – то есть, когда существует хоть малейшая вероятность события. В данном случае носитель можно оценить интервалом: [0; 0,4].

Пример 7. Дана фраза: “Коля сказал, что он немного опоздает, а Слава придёт вовремя”. Расставить актантные индексы.

В первой фразе Коля маркируется как i, а местоимение “он”, могущее относиться к Коле или кому-то другому, как i/j. Слава – новый субъект, которому придаётся новый индекс k. Тот, кто опоздает, не может быть Славой, так как Слава придёт вовремя, поэтому местоимение “он” также снабжается индексом *k. Таким образом, разметка всей фразы выглядит так: “Коля _i сказал, что он _{i/ j/ *k} немного опоздает, а Слава _k придёт вовремя”.