Примеры для самостоятельного решения.

3.1. Даны простые высказывания: A₁ – “ Предложение является простым”, A₂ – “ Предложение осложнено причастным оборотом”, A₃ – “ Предложение осложнено деепричастным оборотом”, A₄ – “ Предложение осложнено сравнительным оборотом”

Описать события с помощью высказываний A_i, i =1,2,3,4:

a) B₁ – “ Предложение является простым, осложнённым деепричастным или сравнительным оборотами ”

b) B₂ – “ Предложение является простым, осложнённым причастным и деепричастным, но не сравнительным оборотами ”

c) B ₃ – “ Предложение является простым, осложнённым или причастным, или сравнительным оборотом ”

d) B₄ – “ Предложение является или простым, или осложнённым одним из трёх видов оборотов: причастным или деепричастным или сравнительным ”

e) B₅ – “ Предложение является простым, осложнённым хотя бы одним оборотом: причастным, деепричастным или сравнительным ”

3.2. Дано сложное высказывание: “ Если сдам экзамен, отпраздную успех в кафе, а если не сдам экзамен, пойду в библиотеку за учебниками ”. Введём простые высказывания: 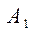- “ Сдам экзамен”, - “ Отпраздную успех в кафе ”, - “ Пойду в библиотеку за учебниками”. Построить логическую схему предложения.

3.3. Дано сложное высказывание: “ Если друг не придёт в гости и мне не позвонят с работы, то либо схожу в музей, либо прогуляюсь по городу ”. Введём элементарные высказывания: A₁ – “ Друг придёт в гости”, A₂ – “ Мне позвонят с работы ”, A₃ – “ Схожу в музей”, A₄ - “ Прогуляюсь по городу”. Построить логическую схему предложения.

3.4. Дано сложное высказывание: “ Необходимо запомнить этот афоризм или записать его в блокнот, но не путать его с похожими афоризмами ”. Введём простые высказывания: A₁ –“ Запомнить этот афоризм”, A₂ – “ Записать его в блокнот ”, A₃ – “ Перепутать его с похожими афоризмами”. Построить логическую схему предложения.

3.5. Дано сложное высказывание: “ Он может перепутать аудитории или забыть подготовить презентацию, но через полчаса он должен прийти ”. Введём простые высказывания: A₁ – “ Он путает аудитории”, A₂ – “ Он помнит о подготовке презентации ”, A₃ – “ Он приходит через полчаса”. Построить логическую схему предложения.

3.6. Введя простые высказывания о взаимном расположении корня и аффикса, описать префикс, суффикс, инфикс и циркумфикс.

3.7. Введя простые высказывания о глагольном времени в простом предложении, описать согласование времён в английском и французском языках.

3.8. Введя простые высказывания о фонетической структуре слова, описать появление на конце слова буквы “ ъ ” в русской дореволюционной орфографии.

3.9. Введя простые высказывания о чередовании ударных и безударных слогов, описать дольник в русской поэзии.

3.10. Пусть A – множество слов китайского языка, B – множество слов монгольского языка, C – множество слов бирманского языка, а x означает тон. Найти характеристические функции .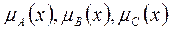

3.11. Пусть x означает артикль, изменяющийся по роду, числу и падежу. Придумать такое языковое множество A, что .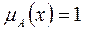

3.12. Дана фраза из СМС, в спешке написанная с сокращениями: “Купи см., прих. домой, пр. с тел.”. Найти возможные варианты прочтения этой фразы и функцию принадлежности этих вариантов.

3.13. Дана фраза из СМС, в спешке написанная с сокращениями: “В ср. сл. кон., нет уч.” Найти возможные варианты прочтения этой фразы и функцию принадлежности этих вариантов.

3.14. У слова много значений. Найти функцию принадлежности числа значений слова. Проверить нормальность и унимодальность множества.

3.15. В шестисловной японской фразе почти не встречается слов, записанных катаканой. Найти функцию принадлежности числа букв слова. Построить дополнение множества.

3.16. В пятисловной фразе примерно одинаковое число неизменяемых (множество A) и двухсложных слов (множество B), одно же слово изменяемо. Найти функции принадлежности числа слов множеств A, B, , 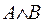. Проверить нормальность и унимодальность множеств.

3.17. Среди шести языков не менее половины относится к одному ареалу (множество A), а несколько языков обладают сходной типологией (множество B). Найти функции принадлежности числа языков множеств A, B, , .

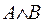3.18. Среди семи письменностей меньшинство является фонетическими (множество A), а большинство в настоящее время уже не используется (множество B). Найти функции принадлежности числа письменностей множеств A, B, , .

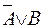3.19. Придумать нечёткое множество A, построить его дополнение ипроверить выполнение условий, присущих чётким множествам: 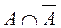= Ø, 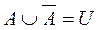, где U – универсальное множество.

3.20. Найти носители нечётких высказываний: “Лёша, вероятно, успеет на матч, Серёжа из-за этих пробок вряд ли успеет, Вадим – возможно, тоже успеет, а насчёт Юры трудно сказать: 50 на 50!”

3.21. Придумать такое нечёткое высказывание A, что Supp A = [0,1; 0,3] 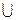[0,7, 0,9].

3.22. Дана фраза: “У моей подруги есть знакомая-врач, а сестра её – парикмахер”. Расставить индексы референции.

3.23. Дана фраза: “Сергей сослался на него в своей статье, опубликованной в его журнале”. Расставить индексы референции.

3.24. Дана фраза: “Он сказал, что сосед его крепко спит, а друг его, наверно, уже ушёл”. Расставить индексы референции.

Отображения.

Пусть дано отображение из множества U во множество V, A: U → V. Образом отображения называется его область значений: Im A = 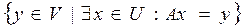. Рангом отображения называется размерность его образа: r(A) = dim (Im A). Ядром отображения A называется полный прообраз нулевого подпространства 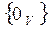: Ker A = 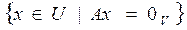. Дефектом линейного отображения называется размерность его ядра: d (A) = dim (ker A). Инвариантом называется множество элементов, не меняющихся при отображении, Inv A = 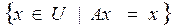. Отображение, все элементы которого являются инвариантами, называется тождественным.

Отображение U → V называется инъективным, если различным элементам из U соответствуют различные элементы в V. Отображение U → V называется сюръективным, если каждый элемент из V соответствует какому-то элементу из U. Отображение U → V называется биективным, если оно является и сюръективным, и инъективным. Размерностью конечных множеств является число их элементов.

Графиком отображения A: U → V называется множество Gr_A = .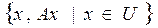

Если отображение A: U → V является биективным, то существует обратное отображение A ^-1: V → U.

Во многих лингвистических задачах (например, переводе фразы) встречается композиция нескольких отображений. Эти отображения связывают между собой различные языковые уровни: фонетический, лексический и грамматический (в котором можно выделить морфологический, синтаксический и словообразовательный подуровни), а также графический. Если в таком процессе участвует несколько языков, то уровни каждого языка следует учитывать отдельно.

Пример 1. Английское слово though транскрибируется как

[ðou]. Найти образ, ранг, дефект, ядро, инвариант и график отображения (слово → транскрипция). Проверить его инъективность и сюръективность.

Запишем отображение в развёрнутом виде: t → ð, h → ð, o → o, u → u, g → Ø, h → Ø, Ø означает нулевой элемент. Образом является транскрипция {ð, o, u}, ранг отображения равен количеству букв образа: r(A) = 3, ядро составляет множество нечитаемых букв {g, h}, а дефект – количеству букв ядра: d(A) = 2. Инвариантом является множество букв, сохраняющих своё чтение: Inv A = {o, u}. Графиком отображения являются пары: t ð, h ð, o o, u u, g Ø, h Ø. Отображение не является инъективным (а, значит, и биективным), так как два элемента t и h отображается в один элемент ð. А сюръективность выполняется, так как каждой букве транскрипции соответствует хотя бы одна из букв слова.

Пример 2. Дано задание: “Транслитерировать и транскрибировать латиницей слово с языка хинди: हैं ” Установить структуру отображения уровней этого задания.

При транслитерации слов один графический уровень отображается в другой графический уровень, а при транскрипции – в фонетический уровень. Поэтому это отображение является биграфо-фонетическим.

Пример 3. Дано задание: “Перевести письменно фразу İki saat sonra dönerim с турецкого языка на русский и французский языки”. Установить структуру отображения уровней этого задания.

Перевод фразы является задачей лексико-грамматической, причём учитывается количество языков. Поскольку перевод является письменным, то добавляются и два графических уровня (кириллица – для русского языка, латиница – для турецкого и французского языка). Значит, отображение является трилексико-триграмматическо-биграфическим.