Урок 189-190 19.10.2021
Задание: проработать материал урока, выполнить д/з.
Обратная связь: работы присылать личным сообщением ВК
Тема урока: Сложение и вычитание векторов. Сумма нескольких векторов
Цели урока:
1) повторить теоретические сведения по теме, изученные в курсе планиметрии;
2) рассмотреть правила треугольника и параллелограмма сложения векторов в пространстве, законы сложения векторов;
3) обратить внимание учащихся на два способа построения разности двух векторов;
4) изучить правило сложения нескольких векторов в пространстве и его применение при нахождении векторных сумм, не прибегая к рисункам.
Ход урока
1. Даны векторы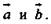 
Построить вектор 
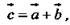пользуясь правилом треугольника.
2. Рассказать правило треугольника.
3. Упростить выражение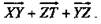 
Вопросы:
- Что называется вектором в пространстве? Его обозначения.
- Что называется длиной вектора? Ее обозначение.
- Какой вектор называется нулевым?
- Какие векторы называются коллинеарными?
- Какие векторы называются сонаправленными? Обозначение.
- Какие векторы называются противоположно направленными? Обозначение.
- Какие векторы называются равными?
Изучение нового материала
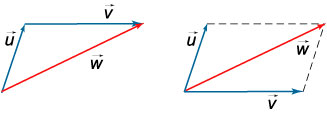
1. Суммой двух векторов u и v называется третий вектор w, проведенный из начала u к концу v, если начало вектора v совпадает с концом вектора u. Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма. w=u+v
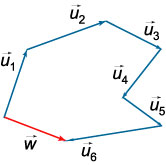
2. Суммой нескольких векторов u1,u2, u3,… называется вектор w, получающийся в результате последовательного сложения данных векторов. Такая операция выполняется по правилу многоугольника. w=u1+u2+u3+…+un
3. Коммутативный закон сложения u+v=v+u
4. Ассоциативный закон сложения (u+v)+w=u+(v+w)
5. Сумма векторов в координатах При сложении двух векторов соответствующие координаты складываются. u+v=(X1+X2,Y1+Y2,Z1+Z2)
6. Разностью двух векторов u и v называется вектор w при условии: w=u−v, если w+v=u
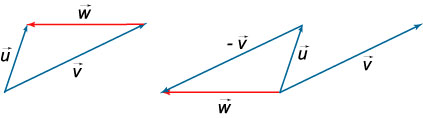7. Разность векторов u и v равна сумме вектора u и противоположного вектора −v: u−v=u+(−v)
8. Разность двух одинаковых векторов равна нулевому вектору: u−u=0
9. Длина нулевого вектора равна нулю: |0|=0
10. Разность векторов в координатах При вычитании двух векторов соответствующие координаты также вычитаются. u−v=(X1−X2,Y1−Y2,Z1−Z2)
|
Опорная схема по теме «Сложение и вычитание векторов»
1. Сумма и разность векторов:
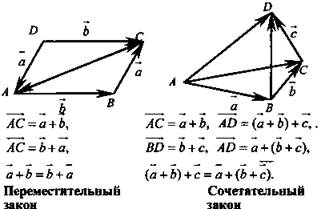
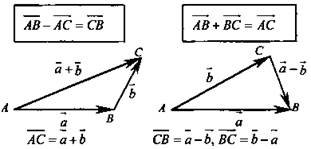2. Законы сложения векторов:
| 
|
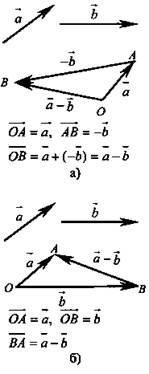
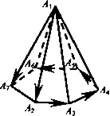
| Правило многоугольника можно сформулировать также следующим образом: если 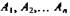 - произвольные точки, то 
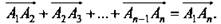Это правило проиллюстрировано на рисунке для т = 7. Отметим, что если точки А1 и Аn, то есть начало первого вектора и конец последнего, совпадают, то сумма векторов равна нулевому вектору.
|
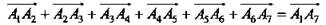
Закрепление изученного материала
Примеры плоских задач на сложение и вычитание векторов
Пример 1. Найти сумму векторов a = {1; 2} и b = {4; 8}.
Решение:
a + b = {1 + 4; 2 + 8} = {5; 10}
Пример 2. Найти разность векторов a = {1; 2} и b = {4; 8}.
Решение:
a - b = {1 - 4; 2 - 8} = {-3; -6}
Примеры пространственных задач на сложение и вычитание векторов
Пример 3. Найти сумму векторов a = {1; 2; 5} и b = {4; 8; 1}.
Решение:
a + b = {1 + 4; 2 + 8; 5 + 1} = {5; 10; 6}
Пример 4. Найти разность векторов a = {1; 2; 5} и b = {4; 8; 1}.
Решение:
a - b = {1 - 4; 2 - 8; 5 - 1} = {-3; -6; 4}
Примеры задач на сложение и вычитание векторов с размерностью большей 3
Пример 5. Найти сумму векторов a = {1; 2; 5; 9} и b = {4; 8; 1; -20}.
Решение:
a + b = {1 + 4; 2 + 8; 5 + 1; 9 + (-20)} = {5; 10; 6; -11}
Пример 6. Найти разность векторов a = {1; 2; 5; -1; 5} и b = {4; 8; 1; -1; 2}.
Решение:
a - b = {1 - 4; 2 - 8; 5 - 1; -1 - (-1); 5 - 2} = {-3; -6; 4; 0; 3}
Домашнее задание: конспект