Упражнение 4.5. Разработайте опросный лист по изучению

Таблица 4.1

№ п/п	Вопросы	Ответы
	_________________________________	_______________________________
	_________________________________	_______________________________
	_________________________________	_______________________________
	_________________________________	_______________________________
	_________________________________	_______________________________

Тема 5. Критерии согласия

Упражнение 5.1. Пользуясь критериями согласия Колмогорова, Романовского, c² (критерий Пирсона), установите, согласуются ли данные наблюдений о росте N мужчин с предположением о распределении роста мужчин по нормальному закону.

Таблица распределения мужчин по росту.

Таблица 5.1.

Рост, см	Число мужчин	Рост, см	Число мужчин
менее 143		164-167
143-146		167-170
146-149		170-173
149-152		173-176
152-155		176-179
155-158		179-182	№
158-161		182-185
161-164		185-188

 

Для нахождения теоретических частот распределения заполните таблицу 5.2.

Таблица расчета теоретических частот.

Таблица 5.2.

Рост, см	частота	Середина интервала
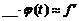
менее 143
143-146
146-149
149-152
152-155
155-158
158-161
161-164
164-167
167-170
170-173
173-176
176-179
179-182
182-185
185-188
Итого

 

=

 

=

 

 

Для нахождения теоретических частот используем формулу

, или ,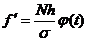

 

где - нормированные отклонения от средней, т.е. и

- основные параметры кривой нормального распределения,

h – длина интервала,

N – общее число измерений.

1. Критерий Пирсона: .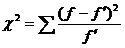

 

Расчет этого критерия проведите в следующей таблице.

Таблица расчета наблюдаемой статистики Пирсона.

Таблица 5.3.

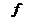
Итого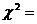

 

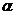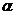В рассматриваемом примере ряд имеет ____ групп (классов) вариантов, следовательно, и_____ групп частот. Поэтому число степеней свободы для последних (при выравнивании по кривой нормального распределения) = =. Примите наиболее часто используемый уровень значимости =0,05. По таблице значений - критерия Пирсона для степеней свободы = и уровня значимости =0,05 определите _табл=. Так как полученное в задаче фактическое значение _факт=, т.е. ___________ табличного, то, следовательно, можно считать _____________ расхождения между эмпирическими и теоретическими частотами и выдвинутая гипотеза о близости эмпирического распределения к нормальному_____________________________________.

Примените критерий Романовского:

Поскольку _____________3, то можно считать расхождения между эмпирическими и теоретическими частотами __________________.

Попробуйте проверить гипотезу с помощью критерия Колмогорова . Для этого запишите накопленные частоты эмпирического и теоретического распределений и найдите максимальный разрыв между ними:

Таблица расчета наблюдаемой статистики Колмогорова.

Таблица 5.4.

		Накопленные частоты
эмпирические	теоретические

 

Максимальный разрыв =, поэтому =.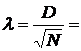

 

 

По таблицам находите для =____, что =. Следовательно, вполне можно полагать, что расхождения между и 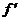носят ____________ характер.

 

Упражнение 5.2. Пользуясь критериями согласия Колмогорова, Романовского, c², установите, согласуются ли данные наблюдений о выезде N автобусов на линию в течение 80+№ дней с предположением о распределении числа неисправных автобусов по закону Пуассона (для этого необходимо вычислить вероятности и теоретические частоты числа неисправных автобусов).

Таблица показателей работы автобусов.

Таблица 5.5.

Число неисправных автобусов (х)
Число дней (f)			№

 

Для решения задачи требуется: 1) вычислить вероятности и теоретические частоты числа неисправностей, считая, что распределение последних подчиняется закону Пуассона; 2) оценить близость эмпирических и теоретических частот с помощью критериев Пирсона, Романовского и Колмогорова.

 

Рассчитайте среднее число неисправностей:

.

Найдите по таблицам значение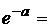

Подставляя в формулу значения =0, 1, 2, 3, 4, 5, получите вероятности числа неисправностей от 0 до 5.

Умножив последние на N (общее число единиц распределения), получите теоретические частоты числа неисправностей, т.е.

Значения 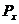и 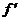(округленные до целого числа) запишите в приводимой ниже таблице:

Таблица теоретических частот.

Таблица 5.6.

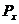
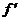	(теоретические частоты) = ___
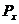
Итого

 

Для оценки близости эмпирических и теоретических частот воспользуемся критериями Пирсона, Романовского и Колмогорова.

 

1. Критерий Пирсона:

 

Проведите расчеты в таблице 5.7.

 

 

Таблица расчета наблюдаемой статистики Пирсона.

Таблица 5.7.

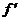
Итого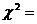

 

Фактическое значение

Находим критическое (табличное) значение при =6-2=4 и 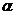=0,05, _табл=9,49. Так как _{факт табл} , т.е. _________________, то имеем все основания считать расхождения между эмпирическими и теоретическими частотами _________________, а следовательно, ___________________ гипотезу о том, что распределение числа неисправностей подчиняется закону Пуассона.

 

Б. Примените критерий Романовского: .

Следовательно, расхождения ____________________.

 

В. И, наконец, по критерию Колмогорова:

Таблица расчета наблюдаемой статистики Колмогорова.

Таблица 5.8.

Накопленные частоты
эмпирические	теоретические

 

Таким образом,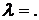

По таблице Приложения 6 найдите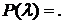

Следовательно, расхождения ____________________.

Выводы (экономическая интерпретация):

1._____________________________________________________________________

 

2.______________________________________________________________________

Тема 6. Изучение динамики общественных явлений

 

Упражнение 6.1. Производство электроэнергии электростанциями региона "Н" характеризуется следующими данными:

Выпуск электроэнергии в регионе "Н"

Таблица 6.1.

Год	Производство электроэнергии, млрд. квт. ч
	№
	27,6
	26,1
	27,4
	26,8
	27,1
	28,6
	30,5
	32,2

Для анализа ряда динамики определите:

1. показатели, характеризующие динамику производства энергии: абсолютный прирост, ускорение, темпы роста и прироста. Результаты расчетов изложите в табличной форме (табл. 6.2.).

2. средний уровень ряда динамики, средний абсолютный прирост, средний темп роста, средний темп прироста.

Для определения основной тенденции ряда произведите выравнивание ряда динамики с помощью метода скользящей средней с тремя и пятью членами.

Сравните первоначальный и выровненный ряды с помощью линейной диаграммы.

По результатам задачи сделайте выводы.

Показатели динамики производства электроэнергии региона "Н"

Таблица 6.2.

Производство Электроэнергии млрд. квт. ч	Абсолютный Прирост, Млрд. квт. ч	Ускоре ние, млрд. квт.ч	Темпы роста, %	Темпы прироста, %
	Цепной способ	Базисный способ		Цепной способ	Базисный способ	Цепной способ	Базисный способ	Значение 1% прироста
27,6
26,1
27,4
26,8
27,1
28,6
30,5
32,2

Средние показатели динамического ряда:

 

Среднее значение__________________________________________________________

 

Средний абсолютный прирост_______________________________________________

 

Среднегодовой темп роста___________________________________________________

 

Среднегодовой темп прироста________________________________________________

 

У пражнение 6.2. Выровняйте представленный в таблице 6.1. динамический ряд методом скользящей средней по три и пять членов.

Таблица 6.3.

Год	Уровень показателя	Сумма трех членов	Скользящая средняя	Сумма пяти членов	Скользящая средняя
	27,6
	26,1
	27,4
	26,8
	27,1
	28,6
	30,5
	32,2

Выводы:

1._____________________________________________________________________

 

2.______________________________________________________________________

 

Результаты фактические и выровненные изобразите на графике.

 

Рис. 6.1.

Упражнение 6.3. В течение двух лет предприятие имело следующие объемы потребления электрической энергии.

Таблица потребления электроэнергии.

Таблица 6.4.

Номер месяца	2001г. млрд. квт.	2002г. млрд. квт.	Итого за месяц	среднее за месяц	абсолютное отклон.	индекс сезонности
	145.4 - №/10	152.3
	134.6	149.9
	131.8	147.5
	112.7	144.8
	101.4	142.8
	111.3	139.4
	119.6	142.2
	125.9	144.5
	129.2	147.9
	137.6	150.2
	122.5	148.3
	127.9	144.7 + №/20

Для указанных рядов динамики:

1. Заполнив таблицу 6.4, выявите наличие сезонной неравномерности методами:

а) конечных разностей; б) индексов сезонности.

Сделайте выводы по первому пункту упражнения:

1._____________________________________________________________________

 

2.______________________________________________________________________

 

2. Постройте модель сезонной волны, используя выравнивание второго ряда методом Фурье (1 гармоника). Для решения задачи заполните таблицу 6.5.

Таблица индексов сезонности Таблица 6.5.

Месяцы	y	t	y*cos(t)	y*sin(t)		(%)
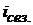Январь	152.3
Февраль	149.9	π/6
Март	147.5	π/3
Апрель	144.8	π/2
Май	142.8	2π/3
Июнь	139.4	5π/6
Июль	142.2	π
Август	144.5	7π/6
Сентябрь	147.9	4π/3
Октябрь	150.2	3π/2
Ноябрь	148.3	5π/3
Декабрь	152,6	11π/6
Итого

Найдите параметры уравнения:

Уравнение модели будет иметь такой вид:

=

 

3. Определите индексы сезонности по формуле:

 

4. Определите среднее квадратическое отклонение индексов сезонности.

 

=

 

 

5. Для первого ряда найдите коэффициент автокорреляции. Для этого сначала заполните таблицу 6.6.

Таблица расчета коэффициента автокорреляции.

Таблица 6.6.

				*
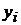
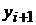
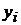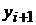
Итого

 

Затем рассчитайте коэффициент автокорреляции.

 

 

 

Сделайте выводы:

 

1._______________________________________________________________________

2. ________________________________________________________________________

Тема 7. Индексы

Упражнение 7.1. Используя данные таблицы 7.1., рассчитайте индивидуальные и агрегатные индексы объема, цены и себестоимости.

Таблица характеристик продуктов.

Таблица 7.1.

Продукты	Базисный период	Отчетный период
Объем, кг q0	Цена, руб. p0	Себестои-мость,руб. z0	Объем, кг q1	Цена, руб. p1	Себестои-мость,руб.z1
А		2*№	2*№-1		2*№+2	2*№-1
Б
В

 

1 Индивидуальные индексы

 

 

 

 

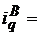
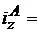
2. Агрегатные индексы (обозначения: Л, П – индексы соответственно Ласпейреса и Пааше)

 

Вывод________________________________________________________________

 

 

Вывод________________________________________________________________

 

 

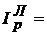
Вывод________________________________________________________________

 

 

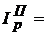
Вывод________________________________________________________________

 

 

Вывод________________________________________________________________

 

 

 

Вывод________________________________________________________________

Выводы (экономическая интерпретация):

1._____________________________________________________________________

 

2.______________________________________________________________________

 

Упражнение 7.2. Используя данные таблицы 7.2., оцените работу отделов маркетинга и сбыта предприятия по следующим показателям:

1) суммарная выручка, как по отдельным странам, так и в совокупности;

2) индексы товарооборота;

3) абсолютные показатели изменения товарооборота за счет изменения цен и физического объема;

4) индекс фиксированного состава;

5) индекс переменного состава;

6) индекс структурных сдвигов.

Таблица результатов внешнеторговой деятельности.

Таблица 7.2.

Страна-импортер	Объёмы поставок, шт.	Внешнеторговая цена, дол.
Базисный период	Отчетный период	Базисный период	Отчетный период
Индия
Франция
Турция	№*10	№*20
Итого

 

1.

 

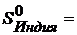
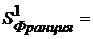
2.

 

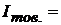
3.

 

 

4.

 

 

 

 

 

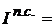
Выводы (экономическая интерпретация):

1._____________________________________________________________________

 

2.______________________________________________________________________

 

Упражнение 7.3. По данным таблицы 7.1. рассчитайте:

 

- агрегатный индекс цены как средний гармонический индекс цены

 

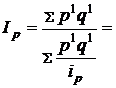
- агрегатный индекс физического объема как средний арифметический индекс физического объема

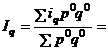
Тема 8. Статистическое изучение взаимосвязей

 

По 20 предприятиям по производству телевизоров были установлены затраты на рекламу (первый факторный признак), объем основных производственных фондов (второй факторный признак) и количество проданной продукции в тысячах штук (результативный признак). В таблице предприятия ранжированы по величине затрат на рекламу.

Таблица продаж телевизоров.

Таблица 8.1.

Порядковый номер предприятия	Затраты на рекламу в тыс. условных единицах,	Объем основных производственных фондов, млн. у.е.	Количество проданных телевизоров, тыс. шт.	Порядковый номер предприятия	Затраты на рекламу в тыс. условных единицах,	Объем основных производственных фондов, млн. у.е.	Количество проданных телевизоров, тыс. шт.
	№+1				№+5
	№+1				№+5
	№+2				№+6
	№+2				№+6
	№+2				№+6
	№+3				№+7
	№+3				№+7
	№+4				№+7
	№+4				№+8
	№+4				№+8

Упражнение 8.1. Определите наличие или отсутствие связи между затратами на рекламу и объемом продажи телевизоров путем построения:

- поля корреляции;

- групповой таблицы.

Рис 8.1. Поле корреляции между Y и X₁.

 

Вывод________________________________________________________________

 

Заполните групповую таблицу

Таблица распределения предприятий по группам

Таблица 8.2.

Группы заводов по затратам на рекламу, тыс. у.е.	Число фирм в группе	Среднее число проданных телевизоров по группе, тыс.шт.
Итого

Вывод________________________________________________________________

Упражнение 8.2. Оцените тесноту корреляционной связи между затратами на рекламу и объемом продажи телевизоров с помощью:

- коэффициента корреляции знаков (Г. Фехнер);

- парного коэффициента корреляции.

Сначала вычислите

 

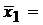
Таблица расчета коэффициента Фехнера.

Таблица 8.3.

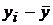
Порядковый номер предприятия	Затраты на рекламу в тыс. условных единицах,	Количество проданных телевизоров, тыс. шт.	Знак	Знак	Совпадение или несовпадение знака

Тогда

 

К_ф=

 

Вывод _______________________________________________________________

 

 

Вычислите коэффициент парной корреляции

 

=

 

 

Упражнение 8.3. Найдите коэффициенты линейного уравнения регрессии для затрат на рекламу и объемом продажи телевизоров. Определите коэффициент эластичности и сделайте вывод о связи затрат на рекламу и объемом продаж телевизоров.

Вычислите

 

 

Запишите уравнение регрессии

 

y=b*x+a=

 

Найдите коэффициент эластичности

 

 

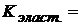
Вывод___________________________________________________________________

 

Упражнение 8.4. По данным 10 предприятий (графы 1 и 2 приводимой ниже таблицы) с помощью коэффициентов корреляции рангов Спирмэна () и Кендэла (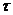) измерить тесноту зависимости между объемом выпуска продукции (у), млн. руб., и стоимостью основных производственных фондов (х), млн. руб.

 

 

Таблица расчета показателей ранговой корреляции. Таблица 8.5.

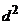
х	у					Подсчёт баллов
«+»	«-»
1.5	№/10
1.8	4.4
2.0	3.8
2.2	3.5

⇐ Предыдущая12

Поделиться: