У этого типа ЛЗ полностью снимается проблема АЧХ. Действительно, ОПФ фазового звена имеет вид
Следовательно,
Решая задачу синтеза ЛЗ на фазовых звеньях, необходимо найти такой полином Гурвица 
, у которого в заданном интервале частот функция 
аппроксимировала бы линейную зависимость 
.
Интервал аппроксимации чаще всего ограничивается полосой частот 
, что характерно для ЛЗ видеосигналов.
Для того чтобы решение было общим для любых конкретных значений 
аппроксимируемой функции 
удобно от переменной 
перейти к нормированной частоте 
, где 
– нормирующая частота, и нормированному времени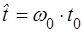 
При этом аппроксимируемая функция переходит в функцию 
, а интервал аппроксимации – в интервал 
. Обозначим 
. Тогда 
, а аппроксимирующая функция будет иметь вид:
В свою очередь, учитывая свойства реактансных функций последнее выражение можно записать в виде
где 
,
Н – некоторая функция.
а) Интерполирование линейной фазы
Для приближенного воспроизведения заданной линейной зависимости 
можно применять интерполирование, расположив узлы интерполяции в n равностоящих точках 
. Такие же значения будут принимать в этих точках аппроксимируемая 
и аппроксимирующая 
функции. Для получения указанных значений под знаком 
должны чередоваться ноль и полюс, то есть числитель и знаменатель должны поочередно обращаться в ноль.
В таком случае, например, при четырех узлах интерполирования 
и Н > 0, аппроксимирующая функция будет иметь вид
Значение Н можно найти, если потребовать, чтобы в точке 
производная функции 
совпадала бы со значением производной 
. В рассматриваемом примере 
, а при малых
|
|
, то 
.
Приравняв это значение к единице, получим:
График полученной функции
Рисунок 5
Числитель найденной функции представляет собой нечетную, а знаменатель – четную части комплекса полинома Гурвица. Поэтому
Собственно же полином Гурвица от нормированного переменного 
имеет вид
б) Линии задержки с равноволновыми частотными характеристиками
Из рисунка 5 нетрудно заметить, что отклонения аппроксимируемой функции и аппроксимирующей функции между узлами неодинаково. Поэтому найденное методом интерполирования решение, хотя и удовлетворительно воспроизводит заданную зависимость, следует рассматривать как первое приближение, которое затем можно уточнить.
Трифоновым И.И. с помощью ЭВМ была найдена совокупность полиномов Гурвица различных степеней n, у которых функция 
аппроксимирует линейную зависимость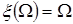 
с минимальной в смысле Чебышева погрешностью. Например, полином четвертой степени имеет вид
График разности 
показан на рисунке 6.
Рисунок 6
в) Линии задержки с монотонными частотными характеристиками.
Другим способом аппроксимации фазы является аппроксимация по Тейлору. В этом случае функции 
для точки 
находятся аналитически и включают в себя так называемые полиномы Бесселя, как разновидность полиномов Гурвица
и т. д. (см. справочную литературу).
Полиному Бесселя 
степени n соответствует функция 
, которая в точке 
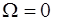разлагается в ряд
,
где 
есть коэффициенты ряда, которые выражаются через функции Бесселя, чем и обусловлено название рассматриваемых полиномов.
|
|
На рисунке 7 приведены графики 
для нескольких полиномов Бесселя младших степеней, а на рисунке 8 графики 
, аппроксимирующие постоянное групповое время
Рисунок 7
Рисунок 8
Из рисунка 8 видно, что частотные зависимости группового времени прохождения ЛЗ являются максимально плоскими. Из него также видно, что интервал аппроксимации увеличивается с ростом степени полинома, а погрешность приближения монотонно возрастает с ростом 