Этапы вероятностно-статистического моделирования

 

 

Необходимо выделить следующие основные этапы построения вероятностно-статистической модели:

1) Постановочный этап. Он должен включать конечные прикладные цели моделирования, набор факторов, переменных, описание взаимосвязей между ними, роль этих факторов. Эти факторы могут быть входными – то есть такие, которые легко поддаются регистрации и прогнозу; а также выходными – они обычно трудно поддаются непосредственному прогнозу, их значения формируются непосредственно в процессе функционирования моделируемой системы.

2) Априорный, предмодельный – он заключается в анализе сущности моделируемого явления, формировании и формализации имеющейся исходной информации об этом явлении, представлении её в виде гипотез и исходных допущений. Гипотезы должны быть подтверждены теоретическими рассуждениями о механизме изучаемого явления.

3) Информационно-статистический – здесь производится сбор необходимой информации о моделируемом явлении, представление её в удобном для использования виде.

4) Спецификация модели – включает в себя непосредственный вывод общего вида модельных отношений, которые связывают между собой входные и выходные переменные. Следует отметить, что на этом этапе будет определена лишь структура модели, её аналитическая запись.

5) Идентифицируемость и идентификация модели – на данном этапе происходит статистический анализ модели с целью правильного внедрения в неё исходных статистических данных, которыми мы располагаем. Если данных, полученных на предыдущем этапе достаточно, то можно решать проблему идентификации модели, то есть предложить и реализовать математически правильную процедуру оценивания неизвестных значений параметров модели по имеющимся статистическим данным. Если данных недостаточно, то возвращаются к четвертому этапу и вносят необходимые коррективы в решение задачи спецификации модели.

6) Верификация модели – на этом этапе производится статистический анализ точности и адекватности модели. Для этого используются различные процедуры сопоставления модельных заключений, оценок, следствий и выводов с реально наблюдаемой действительностью. При неудачном характере этих экспериментов возвращаются к четвертому этапу, а иногда и к первому.

Построение и анализ модели могут быть основаны только на априорной информации и могут не предусматривать проведение третьего и пятого этапов. Тогда полученная модель не будет являться вероятностно-статистической.

 

3. СРАВНЕНИЕ ПРОЦЕССОВ МОДЕЛИРОВАНИЯ

Необходимо обратить внимание, что успешное проведение априорного этапа моделирования играет ключевую роль в общей оценке степени реалистичности и работоспособности построения модели.

Адекватность и эффективность модели будут очень сильно зависеть от того, насколько глубоко и профессионально был проведён анализ реальной сущности изучаемого явления при формировании исходной информации. Дело в том, что при вероятностно-статистическом моделировании и, особенно, на этапе формирования априорной информации о физической природе реального механизма преобразования входных показателей в выходные часть этого механизма остаётся скрытой от исследователя. Обычно эта часть в кибернетической терминологии носит название «чёрного ящика». Чем точнее исследовано реальное явление, тем меньше будет доля «чёрного ящика» в общей логической схеме моделирования и тем работоспособнее и точнее будет построена модель. «Вероятностно-статистическое моделирование, полностью основанное на логике “чёрного ящика”, позволяет получить исследователю лишь как бы мгновенную «статистическую фотографию » анализируемого явления, в общем случае непригодную, например, для целей прогнозирования».[1]

Напротив, моделирование, которое опирается на глубокий анализ природы изучаемого явления, позволяет очень хорошо теоретически обосновать общий вид конструируемой модели, что позволяет производить по ней правомерные прогнозные расчёты. Однако в отличие от предыдущей модели, она одинаково хорошо может описывать характер распределения, наблюдаемого в различных выборках в одной и той же совокупности.

Может случиться так, что моделируемые значения выходных параметров будут сильно отличаться от тех, что получены в действительности, хотя информационно-статистический этап и этап спецификации модели проведены грамотно и аккуратно. Тогда причина неудовлетворительных результатов может лежать в плохом соблюдении всех (или части) принятых при моделировании в качестве априорных допущений исходных предпосылок. Для решения нужно пересмотреть функционирование всех зависимостей, которые использовались при построении модели. В то же время ошибка может быть результатом вынужденного упрощения механизма моделируемого явления. В этом случае следует усовершенствовать модельные допущения, что приведёт, естественно, к изменению модели.

 

 

Случайные процессы

«Случайным процессом называется семейство случайных величин , заданных на вероятностном пространстве , где T – некоторое множество значений параметра».

Параметр t обычно обозначает время. Если этот параметр принимает дискретные значения (например, е=0,2,…), то X(t) – процесс с дискретным временем (случайная последовательность), если же t изменятся на некотором интервале, то X(t) - процесс с непрерывным временем. Таким образом, если случайные величины семейства принимают дискретные значения, то имеет место процесс с дискретными значениями, если же непрерывные – то с непрерывными значениями.

Пусть существует какая-либо физическая система S, которая с течением времени меняет своё состояние случайным образом. Тогда мы можем говорить, что в системе S протекает случайный процесс.

Под «физической системой» можно понимать, например, какое-либо техническое устройство, целую группу таких устройств, отрасль промышленности, уровень инфляции и тому подобное. Большинству процессов, протекающих в окружающей нас жизни, свойственны, в той или иной мере, черты случайности, неопределённости.

Можно привести несколько примеров: космический корабль, который выводится на заданную орбиту. Этот процесс неизбежно сопровождается случайными ошибками, например, отклонение от заданного курса, который необходимо корректировать уже в процессе полёта. Или осуществление перевозок грузов между предприятиями. Процесс перевозок не застрахован от таких случайных явлений, как поломки транспорта, аварии, перемены погоды.

Гораздо сложнее выделить такой процесс, который полностью лишён случайностей. Даже такой процесс, как ход часов, не является неслучайным, так как возможны, например, уход их вперёд, отставание, остановка.

Таким образом, можно сделать вывод, что всем процессам в природе присущи случайные возмущения. На некоторые процесс она оказывают столь малое влияние, что ими можно пренебречь. Необходимость учёта случайностей возникает тогда, когда они прямо касаются нашей заинтересованности.

 

 

3.2. Марковские случайные процессы и варианты их практического применения

«Случайный процесс, протекающий в системе, называется Марковским, если для любого момента времени t₀ вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент времени t₀ и не зависят от того, когда и как система пришла в это состояние». [3]

В исследовании операций также большое значение имеют Марковские случайные процессы с дискретным состоянием и непрерывным временем. При этом его элементы могут принимать различные состояния S₁,S₂,…,S_m, и переход системы из одного состояния в другое происходит «скачком», практически мгновенно, а моменты возможных переходов этих состояний случайны, так что переход может осуществиться в любой момент времени.

Пример такого процесса: техническое устройство S состоит из двух узлов, каждый из которых в любой момент времени может выйти из строя, отказать. Когда происходит отказ устройства, то сразу же начинается его ремонт. Таким образом, всего возможно четыре состояния такой системы: S₁ – оба узла исправны, S₂ – первый узел ремонтируется, второй исправен, S₃ – второй узел ремонтируется, первый исправен, S₄ – оба узла ремонтируются. При этом переход системы S из состояния в состояние происходит практически мгновенно.

Рассмотрим теперь случайный процесс с дискретным временем и дискретными значениями S₁,S₂,…,S_m, в которых находится элемент процесса. Например, каждый работник предприятия может находиться в одном из следующих состояний: S₁ – работает, S₂ – в командировке, S₃ – в отпуске, S₄ – болен.

В данном случае можно говорить о случайном процессе X(t), в котором X(t) принимает значения того состояния, в котором элемент процесса находится в момент времени t. Рассмотрим моменты t₁,t₂,…t_i,…; X_i=X(t_i) и X_i принимает значения S₁,S₂,…,S_m.

«Простейшим обобщением этого процесса с независимыми значениями является Марковский процесс, для которого

то есть вероятность попасть в состояние в момент зависит не от всего прошлого, а лишь от состояния в котором процесс был в предыдущий момент времени ».[3] Мы также можем получить матрицу P с элементами p_ij, которые являются вероятностями перехода из состояния i в состояние j.

Рассмотрим экономический пример цепи Маркова с конечным множеством состояний. Для некоторых экономических задач (например, энергетики) необходимо знать чередование годов с определёнными значениями годовых стоков рек. Абсолютно точно это чередование определить нельзя. Для определения чередования вероятностей необходимо разделить элементы процесса, введя четыре возможных состояния: первое, второе, третье и четвертое. В результате накопления влаги будем для определённости считать, что за первым состоянием никогда не может следовать четвёртое и наоборот. Допустим, что остальные переходы возможны, тогда:

· из первого состояния можно попасть во вторую и третью градации вдвое чаще, чем в первую и нельзя попасть в четвертую. Вероятности переходов равны

· из четвёртого состояния переходы во второе и третье состояние бывают в четыре и в пять раз чаще, чем возвращение в четвёртое состояние, значит

· из второго состояния переход может быть только реже: в первое – в два раза, в третью – на 25%, в четвёртую – в четыре раза, чем переход во вторую, следовательно

· из третьего состояния переход во второе состояние столь же вероятен, как и возвращение в третье состояние, а переходы в первое и четвертое состояние бывают в четыре раза реже, поэтому:

Таким образом, можно получить матрицу вероятностей переходов для стоков реки:

Если цепь Маркова имеет m состояний, то её строки представляют собой m распределений вероятностей. Для однородных цепей Маркова матрицы вероятности переходов не зависят от времени.

Свойства переходных матриц: все их элементы неотрицательны, и суммы по строкам равны единице. Иногда матрицы с такими свойствами называют стохастическими. С помощью матриц переходов можно вычислять вероятность любой траектории элемента случайного процесса, представляющего собой цепь Маркова.

Для современной экономики математическое моделирование, как дисциплина, очень популярна. Например, используя математическое моделирование можно осуществить проектирование, внедрение и сопровождение финансовых инноваций: новых финансовых стратегий, инструментов и процессов. Так, путём применяя математического аппарата исследования операций, разработана технология управления портфелем ценных бумаг в динамике. Существует предположение, что изменение цен на бумаги от сессии к сессии описывается в виде Марковского процесса с дискретным временем и заданной глубиной памяти.

При реализации этой технологии были получены очень неплохие результату. Практические расчёты проводились в течение одного года на примере государственных краткосрочных облигаций (ГКО). Доходность этих бумаг, таким образом, составила в среднем 14% за год при 8.5% у портфеля в среднем по рынку.

Что касается возможности применения данной конструкции на других рынках, то все определяется конкретной спецификой того или иного сегмента рынка.

 

 

3.3. Регрессионный анализ

 

 

В исследовании экономических явлений очень часто имеющиеся данные могут быть как случайными, так и полностью известными, или если регрессия явно не прямая и тому подобное. В этих случаях всегда необходимо определять кривую, которая даёт наилучшее приближение к исходным данным, используя метод наименьших квадратов. Соответствующие методы приближения получили название регрессионного анализа.

Задачами регрессионного анализаявляются установление форм зависимости между переменными, оценка функции регрессии, оценка неизвестных значений (прогноз значений) зависимой переменной.

Одним из подходов в регрессионном анализе является парная регрессионная модель.

В её основе рассматривается односторонняя зависимость случайной зависимой переменной Y от одной (или нескольких) неслучайной независимой переменной X, называемой часто объясняющей переменной. Такая зависимость может быть представлена в виде модельного уравнения регрессии. Также на парную регрессионную модель могут оказывать воздействие некоторые неучтённые случайные факторы. Из-за этого отдельные наблюдения y будут в большей или меньшей степени отклонятся от функции регрессии . В этом случае уравнение взаимосвязи двух переменных может быть представлено в таком виде:

,

где – случайная переменная, которая характеризует отклонение функции от регрессии. Эту переменную также принято называть возмущением.

Таким образом, в регрессионной модели зависимая переменная Y есть некоторая функция с точностью до случайного возмущения .

Возьмём для примера линейную парную регрессионную модель вида:

,

эта модель содержит n пар значений переменных , где i=1,2,…, n. Можно выделить основные предпосылки регрессионного анализа:

1) Зависимая переменная , а также возмущения есть величины случайные, хотя при этом объясняющая переменная – величина неслучайная.

2) Математическое ожидание возмущения равно нулю.

3) Дисперсия зависимой переменной , а также возмущения постоянная для любого i.

4) Переменные и или возмущения соответственно не коррелированны.

5) Зависимая переменная или возмущение есть нормально распределённые случайные величины.

Для того, чтобы получить уравнение регрессии, достаточно использовать первые четыре предпосылки. Выполнение пятой предпосылки необходимо для оценки точности уравнения регрессии и его параметров.

Оценкой вышеприведённой модели является уравнение регрессии . При этом определение неизвестных параметров b₀ и b₁ осуществляется путём использования метода наименьших квадратов. А неучтённые факторы определяются в модели с помощью остаточной дисперсии .

Рассмотреть все соотношения и связи между социально-экономическими явлениями и процессами далеко не всегда удаётся выразить только линейными функциями из-за того, что могут возникать неоправданно грубые ошибки.

Очень важный этап анализа – это выбор вида уравнения регрессии, он носит название спецификации или этапом параметризации модели. Выбор производится на основании опыта предыдущих исследований, литературных источников, других соображений профессионально-теоретического характера, а также визуального наблюдения расположения точек корреляционного поля. Наиболее распространёнными считаются следующие виды уравнений нелинейной регрессии:

полиномиальные: ,

степенные: ,

гиперболические : .

Каждый из них имеет свои границы применения. Например, если исследуется какой-либо экономический показатель y, который зависит от объема продаваемых товаров x. У x есть также два показателя: первый не зависит от x, а второй уменьшается с ростом x. Тогда зависимость y от x можно представить в виде гиперболы . Полиномы же используются, например, если экономический процесс имеет тенденции к постоянному ускорению или замедлению.

В ряде случаев для адекватного описания экономических процессов используются более сложные функции. Например, в начале процесс может развиваться очень быстро, а затем, по достижении определённого уровня, замедляется и приближается к некоторому пределу. В этом случае полезными могут оказаться логистические функции, например .

Очень часто нелинейные связи возникают из-за объединения в одну совокупность объектов, разного качественного уровня. Например, объединение в одну совокупность предприятий различных отраслей, или же очень сильно отличающихся друг от друга по природным условиям. Здесь нелинейные зависимости возникают вследствие объединения разнородных единиц, и регрессионный анализ таких процессов не может быть эффективным. Поэтому любая нелинейность связей должна критически анализироваться.

Расположение точек корреляционного поля очень важно, но по нему далеко не всегда можно принять окончательное решение о виде уравнения регрессии. В этом случае бывает полезно сделать расчёты по двум или нескольким уравнениям. Предпочтение отдаётся уравнению, для которого меньше величина остаточной дисперсии. Однако при небольшом расхождении в остаточных дисперсиях следует выбирать более простые уравнения.

Весьма интересный приём заключается в использовании полинома для идеального приближения к функции. Можно подобрать полином таким образом, что он пройдёт через все вершины регрессии. Однако это может привести к неоправданному усложнению вида искомой функции регрессии, «когда случайные отклонения осреднённых точек неправильно истолковываются как определённые закономерности в поведении кривой регрессии».[3] В связи с этим в практике регрессионного анализа очень редко используются полиномы выше третьей степени.

Достоинства и недостатки регрессионного анализа приведены в таблице 3.3.1.

 

Таблица 3.3.1

Метод	Достоинства	Недостатки
Регрессионный анализ	1. Простота вычислительных алгоритмов. 2. Наглядность и интерпретируемость результатов (для линейной модели).	1. Невысокая точность прогноза (в основном - интерполяция данных). 2. Частое нарушение основных предпосылок корректности метода. 3. Субъективный характер выбора вида конкретной зависимости (формальная подгонка модели под эмпирический материал). 4. Отсутствие объяснительной функции (невозможность объяснения причинно-следственной связи).

3.4. Множественный регрессионный анализ

 

 

Экономические явления очень часто определяются большим числом одновременно и совокупно действующих факторов. В связи с этим возникает задача исследования зависимости зависимой переменной Y от нескольких переменных X₁,X₂,…,X_n. Эта задача решается с помощью множественного регрессионного анализа.

Для составления модели множественной регрессии необходимо обозначить i -е наблюдение переменной y_i и объясняющих переменных – x_i1,x_i2,…,x_ip. Тогда модель можно представить в таком виде:

где i=1,2,…,n, а является случайным возмущением.

Если в модель включается много объясняющих переменных, это сильно усложняет получаемые формулы и вычисления. Поэтому целесообразным является использование матричных обозначений. Это облегчает как теоретические концепции анализа, так и необходимые расчётные процедуры.

Можно ввести обозначения: – матрица-столбец, или вектор, значений зависимой переменной размера n.

– матрица значений объясняющих переменных, или матрица плана размера .

Модель в матричной форме записывается следующим образом: . Оценкой этой модели по выборке является уравнение

где .

В случае применения в экономике подобных моделей всегда необходимо учитывать, что все входящие в модель факторы по-разному влияют на результат. Некоторые из них оказывают весьма существенное влияние, другие весьма незначительное. «К числу основных факторов при изучении экономического объекта относят обычно настоящий труд (или трудовые ресурсы в той или иной мере), прошлый труд (энергия, сырьё, материалы, оборудование, здания, сооружения и так далее)».[2] Вместе с тем на экономические системы не могут не влиять и природные условия, поэтому в модели должны быть адекватно отражены и эти факторы.

 

3.5. Временные ряды

Под временным рядом в экономике понимается последовательность наблюдений некоторой случайной величины X в одинаковые промежутки времени. Отдельные наблюдения называются уровнями ряда, которые обозначаются x_t (t=1,2,…,n), где n – число уровней.

В качестве примера временного ряда приведены данные в таблице 3.5.1, отражающие цену и спрос товара за пятилетний период времени.

Таблица 3.5.1.

Год, t
Цена, xt
Спрос, yt

 

Как видно, в этой таблице рассматриваются два временных ряда: цены товара x_t и спроса y_t на него.

Обычно при исследовании экономического временного ряда x_t выделяют несколько составляющих:

Рассмотрим все составляющие:

· u_t – тренд, плавно меняющаяся компонента, которая описывает влияние долговременных факторов. Например, экономическое развитие, изменение структуры потребления и тому подобное;

· v_t – сезонная компонента. Она показывает повторяемость экономических процессов в течение не очень длительного промежутка времени. Например, объём продаж товаров в различное время года;

· c_t – циклическая компонента. Она отражает повторяемость экономических процессов в течение длительных периодов времени. Например, влияние волн экономической активности Кондратьева;

· – случайная компонента, отражающая влияние не поддающихся учёту и регистрации случайных факторов.

Необходимо отметить, что в этой модели случайной является только компонента , в то время как другие являются закономерными, неслучайными.

Важнейшей классической задачей при исследовании экономических временных рядов является выявление и статистическая оценка основной тенденции развитии изучаемого процесса.[3]

Основные этапы анализа временных рядов:

· графическое представление временного ряда, описание его поведения;

· выделение и удаление закономерных составляющих временного ряда (тренда, сезонных и циклических составляющих);

· сглаживание ряда, то есть удаление низко- или высокочастотных составляющих;

· исследование случайной составляющей временного ряда, построение математической модели для её описания, проверка адекватности;

· прогнозирование развития изучаемого процесса на основе имеющегося временного ряда;

· исследование взаимосвязей между различными временными рядами.

Наиболее часто применяемые методы анализа временных рядов: корреляционныйи спектральный анализ, модели авторегрессии и скользящей средней.

Различают стационарные временные ряды. Отличие этих рядов заключается в том, что с течением времени, их вероятностные свойства не изменяются. Эти ряды применяются, например, при описании случайных составляющих анализируемых рядов.

«Временной ряд 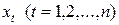называется строго стационарным, если совместное распределение вероятностей n наблюдений такое же, как и n наблюдений при любых n, t и ». [3] То есть, свойства строго стационарных рядов не зависят от момента времени t.

Очень важной задачей при исследовании экономического временного ряда является выделение основной тенденции изучаемого процесса. Эта тенденция выражается неслучайной составляющей f(t). Для решения этой задачи, прежде всего, необходимо правильно выбрать функцию f(t).

Некоторые виды:

линейная:

полиномиальная:

экспоненциальная:

логистическая:

Гомперца:

Выбор подходящей функции – это очень ответственный этап анализа. Нужно правильно установить характер динамики процесса, использовать визуальные наблюдения.

Для выявления основной тенденции чаще всего используется метод наименьших квадратов. Однако применение этого метода для оценки параметров экспоненциальной, логистической функций или функции Гомперца вызывает сложности, связанные с решением получаемой системы нормальных уравнений. Поэтому ещё до получения соответствующей системы, проводят преобразование функций, например, логарифмирование.

Другим методом выравнивания временного ряда является метод скользящих средних. В его основе лежит переход от начальных значений членов ряда к их среднем значениям на определённом интервале времени. При этом сам выбранный интервал времени «скользит» вдоль ряда. Таким образом, получается новый ряд скользящих средних, поведение которого более гладко, чем у исходного ряда. Для усреднения могут быть использованы средняя арифметическая, как простая, так и с некоторыми весами, медиана и другие методы.

Прогнозирование поведения временного ряда является очень важной задачей. Задача прогнозирования ставится следующим образом: имеется временной ряд y_t (t=1,2,…,n) и необходимо получить прогноз уровня этого ряда на момент . Временной ряд можно рассматривать как регрессионную модель изучаемого признака по переменной «время». Соответственно, к такой модели можно применять все те методы, которые используются при регрессионном анализе. Необходимо также отметить, что возмущения (t=1,2,…,n) в регрессионном анализе есть независимые случайные величины с математическим ожиданием, равным нулю. А при работе с временными рядами такое допущение очень часто оказывается неверным.

Например, если вид функции тренда выбран неудачно, то нельзя говорить о том, что отклонения от неё являются независимыми, можно даже говорить о том, что между ними существует взаимосвязь. Если последовательные значения коррелируют между собой, то говорят об автокорреляции возмущений. Это может сильно исказить экономическую модель, поэтому с автокорреляцией возмущений необходимо бороться.

Метод наименьших квадратов также даёт состоятельные оценки параметров при автокорреляции возмущений, однако интервальные оценки могут содержать грубые ошибки. Если автокорреляцию возмущений удаётся выявить, то следует выбрать более удачную функцию тренда, пересмотреть набор включённых в него переменных и тому подобное.

Достаточно надёжным и простым критерием по определению автокорреляции возмущений является критерий Дарбина-Уотсона. С его помощью можно узнать о наличии или отсутствии автокорреляции между соседними остаточными членами ряда e_t и e_t-1, где e_t выборочная оценка .

Значения, которые принимает d заключены в границах от 0 до 4. Когда автокорреляция отсутствует ; при полной положительной автокорреляции ; при полной отрицательной – .

Недостатком критерия Дарбина-Уотсона является наличие области неопределённости критерия, а также то, что значения d -статистики адекватны при рассматривании не менее 15 значений.

Как уже было упомянуто временной ряд содержит как детерминированною, так и случайную составляющие. В экономике роль детерминированной составляющей играет, например, результирующий показатель, который может представлять собой объём производства, который обуславливается общей тенденцией экономического роста, научно-техническим прогрессом и затратами экономических ресурсов. На этот результат кроме экономических факторов могут оказывать влияние и природные, поддающиеся предсказанию, факторы.

Что касается случайной составляющей, то она аккумулирует влияние множества не включённых в детерминированную составляющую факторов, каждый из которых оказывает небольшое влияние на результат.

Основной задачей анализа временного ряда в экономике является выделение детерминированной и случайной составляющих, а также оценка их характеристик. Получив эти оценки, можно очень успешно решать задачи прогноза будущих значений, как самого временного ряда, так и его составляющих.

Таким образом, можно сказать, что временные ряды в экономике успешно применяются, например, для прогнозирования экономических процессов (курсы валют, акций, экономического роста, долей спроса и предложения на различны товары и так далее).

 

3.6. Регрессионные модели

 

 

Каждая ценная бумага – акция, облигация, контракт и другие – в каждый момент времени обладает стоимостью, которая назы­вается курсоми устанавливается рынком. Даже обладая полной информации о выпустившем бумагу эмитенте, однозначно определить ее курс в заданный момент времени в будущем, как правило, оказывается невозмож­ным. В этом случае вполне обоснованно можно рассматривать курс цен­ной бумаги как значение случайной величины X.

Рассмотрим X_t – курс ценной бумаги в момент времени t,тогда X_t+1 – курс в момент времени t+1. Теперь рассмотрим величину

.

Она называется доходностью ценной бумаги. Вполне понятно, что значение именно этой величины определяет привлекательность ценной бумаги для инвестора. И одна из главных задач финансового анализа состоит в возможно более точном предсказании значения величины r

Модели, рассматриваемые в финансовом анализе, связывают случайную величину r с величинами, которые могут объективно охарак­теризовать финансовый рынок в целом. Такие величины носят название факторов.В самом простом случае выделяется один фактор. Тогда ста­тистическая модель принимает вид:

где и – постоянные неизвестные параметры, – слу­чайная величина. Коэффициент называется чувствительностью доходностиценной бумаги к фактору F. Коэффициент называется сдвигом.

В классическом регрессионном анализе значения факторов F считаются детерминированными величинами, таким образом, модель можно представить в виде:

В данной модели t=1,2…,n – моменты времени, которые интерпретируются как номер наблюдения; F₁,..., F_n – известные значения факто­ров; r_t – наблюдаемые выборочные значения случайной величи­ны r; и – неизвестные параметры.

 

 

3.7. Метод планирования экспериментов

 

Экспериментальные методы основаны на сопоставлении данных о входных и выходных сигналах изучаемого объекта. Задачей экспериментальных методов является количественная оценка характеристик конкретных объектов управления (ОУ) и проверка соответствия модели реальному объекту.

Процедуру построения оптимальной в определенном смысле математической модели объекта управления по реализациям его входных и выходных сигналов называют идентификацией ОУ.

Наиболее эффективным подходом к анализу и математическому описанию ОУ является сочетание теоретических и экспериментальных методов исследования.

3.7.1. Сравнительный анализ пассивного и активного эксперимента

Экспериментальные методы описания ОУ делятся на пассивные и активные. В тех случаях, когда по условиям технологического процесса нельзя нарушать режим путем подачи на вход объекта сигналов определенной величины для определения его характеристик, используют метод пассивного эксперимента. Он сводится к регистрации