Задание 22
· РАЗМЕРНОСТЬ И БАЗИС ЛИНЕЙНОГО ПРОСТРАНСТВА.
| Определение | Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов.
Размерность пространства  условимся обозначать через dim. условимся обозначать через dim.
|
| Определение | Векторное пространство  называется n -мерным, если в нем можно найти n линейно независимых векторов, но больше, чем n линейно независимых векторов оно не содержит. называется n -мерным, если в нем можно найти n линейно независимых векторов, но больше, чем n линейно независимых векторов оно не содержит.
|
| Пример | Размерность множества всех плоских векторов равна 2, размерность множества пространственных векторов равна 3. |
| Определение | Пространство, имеющее конечную размерность, называется конечномерным. Пространство, в котором можно найти сколь угодно много линейно независимых векторов, называется бесконечномерным. |
| Определение | Совокупность n линейно независимых векторов n - мерного векторного пространства  называется его базисом. называется его базисом.
|
| Теорема 1 | Каждый вектор  линейного n- мерного пространства линейного n- мерного пространства  можно представить, и притом единственным способом, в виде линейной комбинации векторов базиса. можно представить, и притом единственным способом, в виде линейной комбинации векторов базиса.
|
| Доказательство | Пусть  - произвольный базис пространства - произвольный базис пространства  и и  . Так как любые n+ 1 векторов пространства . Так как любые n+ 1 векторов пространства  линейно зависимы, то зависимы, в частности, и векторы линейно зависимы, то зависимы, в частности, и векторы  , т.е. существуют не равные одновременно нулю числа , т.е. существуют не равные одновременно нулю числа  , такие, что , такие, что
 .
При этом .
При этом  , в противном случае хотя бы одно из чисел , в противном случае хотя бы одно из чисел  было бы отлично от нуля, и вектора было бы отлично от нуля, и вектора  были бы линейно зависимы. Следовательно, были бы линейно зависимы. Следовательно,
 .
Полагая .
Полагая  , будем иметь , будем иметь  .
Это представление .
Это представление  через через  единственно. Доказывается от противного. Числа единственно. Доказывается от противного. Числа  называются координатами вектора называются координатами вектора  в базисе в базисе  . .
|
| Теорема 2 | Если  - линейно независимые векторы пространства - линейно независимые векторы пространства  и любой вектор и любой вектор  линейно выражается через линейно выражается через  , то эти векторы образуют базис в , то эти векторы образуют базис в  . .
|
| Доказательство | Векторы  , по условию, линейно независимы. Покажем, что в пространстве , по условию, линейно независимы. Покажем, что в пространстве  нет более чем n линейно независимых векторов. Выберем произвольные нет более чем n линейно независимых векторов. Выберем произвольные 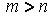 векторов из векторов из  : :  . По условию, каждый из них можно линейно выразить через . По условию, каждый из них можно линейно выразить через  : :
 Рассмотрим матрицу:
Рассмотрим матрицу:
 .
Так как число строк этой матрицы равно n, то ее ранг не больше, чем n, и значит, среди ее столбцов имеется не более, чем n линейно независимых. Но так как m>n, то m столбцов этой матрицы линейно зависимы. Следовательно, линейно зависимы и векторы .
Так как число строк этой матрицы равно n, то ее ранг не больше, чем n, и значит, среди ее столбцов имеется не более, чем n линейно независимых. Но так как m>n, то m столбцов этой матрицы линейно зависимы. Следовательно, линейно зависимы и векторы  . Итак, пространство . Итак, пространство  n – мерно и n – мерно и  - его базис. - его базис.
|
· ПЕРЕХОД К НОВОМУ БАЗИСУ
Пусть в пространстве  имеется два базиса:
имеется два базиса:  и
и  .
.
Первый условимся называть старым базисом, второй – новым. Каждый из векторов нового базиса, по Теореме 1, можно линейно выразить через векторы старого базиса:
 (1)
(1)
Новые базисные векторы получаются из старых с помощью матрицы

При этом коэффициенты их разложений по старым базисным векторам образуют столбцы этой матрицы. Матрица  называется матрицей перехода от базиса
называется матрицей перехода от базиса  к базису
к базису  .
.
Определитель матрицы  не равен нулю, так как в противном случае ее столбцы, а следовательно, и векторы
не равен нулю, так как в противном случае ее столбцы, а следовательно, и векторы  , были бы линейно зависимы.
, были бы линейно зависимы.
Обратно, если  , то столбцы матрицы линейно независимы, и, следовательно, векторы
, то столбцы матрицы линейно независимы, и, следовательно, векторы  , получающиеся из базисных векторов
, получающиеся из базисных векторов  с помощью матрицы
с помощью матрицы  , линейно независимы и значит образуют некоторый базис. Таким образом, матрицей перехода может служить любая квадратная матрица порядка n с отличным от нуля определителем.
, линейно независимы и значит образуют некоторый базис. Таким образом, матрицей перехода может служить любая квадратная матрица порядка n с отличным от нуля определителем.
Рассмотрим теперь, как связаны между собой координаты одного и того же вектора в старом и новом базисах. Пусть  в старом базисе и
в старом базисе и  - в новом. Подставляя в последнее равенство вместо
- в новом. Подставляя в последнее равенство вместо  их выражение из (1), получим, что
их выражение из (1), получим, что

Таким образом, старые координаты вектора  получатся из новых его координат с помощью той же матрицы
получатся из новых его координат с помощью той же матрицы  , только коэффициенты соответствующих разложений образуют строки этой матрицы.
, только коэффициенты соответствующих разложений образуют строки этой матрицы.