Задание 9
· ОДНОРОДНЫЕ СЛАУ
| Определение | Однородной СЛАУ называется система, все правые части которой равны нулю одновременно. |
Однородная СЛАУ, записанная в матричном виде, 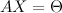 всегда совместна, так как
всегда совместна, так как 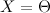 всегда является ее решением.
всегда является ее решением.
Заметим, что если 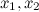 - это два решения однородной СЛАУ, то их линейная комбинация также будет решением однородной СЛАУ:
- это два решения однородной СЛАУ, то их линейная комбинация также будет решением однородной СЛАУ:
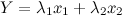
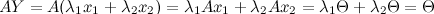
| Теорема | Если однородная квадратная СЛАУ имеет ненулевое решение, то определитель матрицы системы равен нулю. |
| Пример | Задание. Выяснить, имеет ли однородная СЛАУ  ненулевые решения.
Решение. Вычислим определитель матрицы системы: ненулевые решения.
Решение. Вычислим определитель матрицы системы:
 Так как определитель не равен нулю, то система имеет только нулевое решение
Так как определитель не равен нулю, то система имеет только нулевое решение  Ответ. Система имеет только нулевое решение.
Ответ. Система имеет только нулевое решение.
|
· ФУНДАМЕНТАЛЬНАЯ СИСТЕМА РЕШЕНИЙ
| Определение | Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов. |
| Теорема | Общее решение неоднородной СЛАУ равно сумме частного решения неоднородной СЛАУ и общего решения соответствующей однородной СЛАУ. |
| Пример | Задание. Найти общее решение и ФСР однородной системы  Решение. Приведем систему к ступенчатому виду с помощью метода Гаусса. Для этого записываем матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут получаться нули):
Решение. Приведем систему к ступенчатому виду с помощью метода Гаусса. Для этого записываем матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут получаться нули):
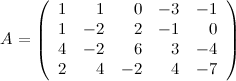 с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду.
От второй строки отнимаем первую,
от третьей - четыре первых,
от четвертой - две первых:
с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду.
От второй строки отнимаем первую,
от третьей - четыре первых,
от четвертой - две первых:
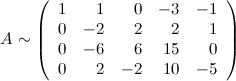 Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого
от третьей строки отнимаем три вторых,
к четвертой прибавляем вторую:
Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого
от третьей строки отнимаем три вторых,
к четвертой прибавляем вторую:
 От четвертой строки отнимем
От четвертой строки отнимем  третьей и третью строку умножим на третьей и третью строку умножим на  : :
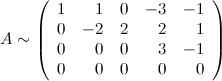 Нулевые строки можно далее не рассматривать, тогда получаем, что
Нулевые строки можно далее не рассматривать, тогда получаем, что
 Далее делаем нули над главной диагональю, для этого
от первой строки отнимаем третью,
а ко второй строке прибавляем третью:
Далее делаем нули над главной диагональю, для этого
от первой строки отнимаем третью,
а ко второй строке прибавляем третью:
 то есть получаем систему, соответствующую данной матрице:
то есть получаем систему, соответствующую данной матрице:
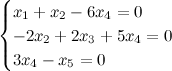 Или, выразив одни переменные через другие, будем иметь:
Или, выразив одни переменные через другие, будем иметь:
 Здесь
Здесь 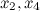 - независимые (или свободные) переменные (это те переменные, через которые мы выражаем остальные переменные), - независимые (или свободные) переменные (это те переменные, через которые мы выражаем остальные переменные), 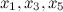 - зависимые (связанные) переменные (то есть те, которые выражаются через свободные).
Количество свободных переменных равно разности общего количества переменных - зависимые (связанные) переменные (то есть те, которые выражаются через свободные).
Количество свободных переменных равно разности общего количества переменных 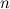 (в рассматриваемом примере (в рассматриваемом примере 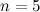 , так как система зависит от пяти переменных) и ранга матрицы , так как система зависит от пяти переменных) и ранга матрицы  (в этом случае получили, что (в этом случае получили, что 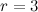 - количество ненулевых строк после приведения матрицы к ступенчатому виду): - количество ненулевых строк после приведения матрицы к ступенчатому виду): 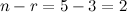 Так как ранг матрицы
Так как ранг матрицы 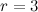 , а количество неизвестных системы , а количество неизвестных системы 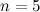 , то тогда количество решений в ФСР , то тогда количество решений в ФСР 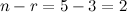 (для проверки, это число должно равняться количеству свободных переменных).
Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки). В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид: (для проверки, это число должно равняться количеству свободных переменных).
Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки). В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:
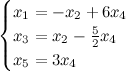 Тогда придавая в первом случае, например, независимым переменным значения
Тогда придавая в первом случае, например, независимым переменным значения  , , 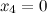 получаем, что получаем, что 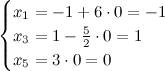 .
Полученные значения записываем в первую строку таблицы. Аналогично, беря .
Полученные значения записываем в первую строку таблицы. Аналогично, беря  , , 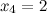 , будем иметь, что , будем иметь, что 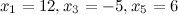 , что и определяет второе решение ФСР. В итоге получаем следующую таблицу: , что и определяет второе решение ФСР. В итоге получаем следующую таблицу:
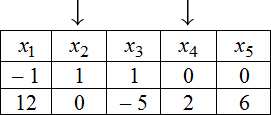 Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:
Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:
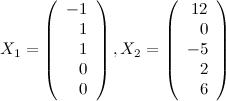 Общее решение является линейной комбинацией частных решений:
Общее решение является линейной комбинацией частных решений:
 где коэффициенты
где коэффициенты  не равны нулю одновременно. Или запишем общее решение в таком виде: не равны нулю одновременно. Или запишем общее решение в таком виде:
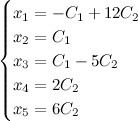 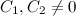 Придавая константам
Придавая константам  определенные значения и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ. определенные значения и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.
|