Введение
ТЕОРИЯ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Линейное программирование - инструмент исследования линейных моделей
Основы симплекс-метода
Симплекс-таблицы
ПРИМЕНЕНИЕ СИМПЛЕКС-МЕТОДА ДЛЯ СОСТАВЛЕНИЯ ПЛАНА ПРОИЗВОДСТВА (НА ПРИМЕРЕ НЭРЗ)
Общая характеристика предприятия
Моделирование экономической ситуации в инструментальном цехе
Решение задачи
ЗАКЛЮЧЕНИЕ
ЛИТЕРАТУРА
Введение
Эффективность работы предприятия зависит от многих факторов, в то числе и от того, как решаются вопросы снижения себестоимости продукции.
Себестоимость продукции находится во взаимосвязи с показателями эффективности производства. Она отражает большую часть стоимости продукции и зависит от изменения условий производства и реализации продукции.
На Новосибирском электровозоремонтном заводе основой планирования и организации производственной деятельности является потребность ОАО РЖД в ремонте подвижного состава, узлов, агрегатов и производства запасных частей по широкой номенклатуре. До настоящего времени загрузка производственных мощностей на предприятии была практически полной, и вопрос использования свободных ресурсов не стоял остро. Теперь же, в связи с падением объема железнодорожных перевозок, и, как следствие, уменьшением количества ремонтируемых электровозов, оптимизация производственного процесса становится существенной необходимостью.
Целью курсовой работы является составление оптимального плана производства дополнительной продукции с использованием симплекс-метода. Для достижения указанной цели необходимо решить следующие задачи:
- изучить теоретические основы линейного программирования,
- применить симплекс-метод для оптимизации плана производства,
Объектом исследования является инструментальный цех филиала ОАО РЖД «Новосибирский электровозоремонтный завод».
ТЕОРИЯ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Линейное программирование - инструмент исследования линейных моделей
В связи с развитием техники, ростом промышленного производства все большую роль играют задачи отыскания оптимальных решений в различных сферах человеческой деятельности. Основным инструментом при решении этих задач стало математическое моделирование - формальное описание изучаемого явления и исследование с помощью математического аппарата.
Всякая модель реального процесса предполагает идеализацию и абстракцию, но они не должны уходить слишком далеко от содержания задачи, чтобы построенная модель не утратила существенных черт моделируемого объекта, т. е. была ему адекватна. С другой стороны, если построить сложную модель, учитывающую все тончайшие особенности изучаемого процесса, то это может нарушить смысл моделирования, одна из целей которого - упростить постановку задачи, чтобы легче было ее исследовать (слишком сложная модель, как правило, не поддается анализу).
В большом числе случаев первой степенью приближения к реальности является модель, в которой все зависимости между переменными, характеризующими состояние объекта, предполагаются линейными. Здесь имеется полная аналогия с тем, как весьма важная и зачастую исчерпывающая информация о поведении произвольной функции получается на основе изучения ее производной - происходит замена этой функции в окрестности каждой точки линейной зависимостью. Значительное количество экономических, технических и других процессов достаточно хорошо и полно описывается линейными моделями. Сказанным определяется важность той роли, которую играет линейное программирование - метод отыскания условного экстремума линейной функции на множестве, заданном при помощи линейных соотношений типа равенств и неравенств (линейных ограничений) [1, с. 9].
Условия применимости линейной модели
Делимость. Если способ применяется с интенсивностями a и b (a < b), то его можно применять с любой интенсивностью x Î [a; b].
Это условие не тривиально. Если, например, интенсивность выполнения работы измерять числом назначенных на нее работников, то допустимы только целые значения интенсивности. Если же интенсивность измеряется числом человеко-часов в сутки, то принцип делимости, по-видимому, выполнен.
Пропорциональность. Затраты, выпуски и полезность, производимые каждым способом, пропорциональны его интенсивности.
Это условие постоянной отдачи (во всех смыслах), отсутствия эффекта масштаба. Особое внимание следует уделять выявлению диапазона интенсивности технологического способа, в котором этот способ удовлетворяет условию пропорциональности. Например, если сварщик проваривает контейнер за 6 часов, то двое сварщиков, пожалуй, справятся с этой работой за 3 часа. Но шестеро - за час - не сварят контейнер.
Аддитивность. Полезности и - для каждого ингредиента - затраты и выпуски, производимые всеми способами, суммируются.
Принцип аддитивности требует аккуратного и согласованного описания входящей в модель номенклатуры: технологических способов, ингредиентов, полезностей.
Формы записи задач линейного программирования
В самом общем виде задача ЛП записывается следующим образом:
1 
(1)
При
2 
(2)
3 
(3)
4 
(4)
5 
(5)
Определение 1. Матрица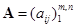 
называется матрицей задачи (1) - (5). □
Более унифицированное представление задачи ЛП - стандартная форма:
При
для i Î {1,…, m}, x ³ 0.
линейный программирование симплекс оптимизация
Особенности стандартной формы: все переменные неотрицательны (n1 = n), ограничения-равенства отсутствуют (m1 = 0). Если ЦФ максимизируется, то m2 = 0 и нет ограничений вида (3); в противном случае m2 = m и нет ограничений вида (4). Полагая 
и 
, стандартную форму можно записать следующим образом:
6c × x ® max (min) при Ax £(³) b, x ³ 0. (6)
Но самый простой вид имеет каноническая форма записи задач ЛП.
Определение 2. Задача (1) - (4) представлена в канонической форме, если все ограничения, кроме условий неотрицательности переменных, являются равенствами (m1 = m) и все переменные неотрицательны (n1 = n). □
Задача ЛП в канонической форме имеет, следовательно, вид
7c × x ® max (min) при Ax = b, x ³ 0. (7)
Основы симплекс-метода
Рассмотрим задачу ЛП в канонической форме:
8 
(8)
при
9 
(9)
10х ³ 0 (10)
Пусть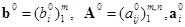 
и 
- соответственно строка i и столбец j матрицы А0. Будем считать, что строки матрицы линейно независимы.
Любую задачу ЛП можно привести к канонической форме; если задача в канонической форме разрешима, то среди ее решений есть хотя бы одна крайняя точка множества допустимых решений; крайние точки множества допустимых решений задачи ЛП в канонической форме совпадают с БДР.
Опираясь на перечисленные факты, можно представить себе следующую процедуру решения задачи. Проверим каким-либо образом, имеет ли задача решение и, если имеет, приведем ее к канонической форме. Пусть матрица А0 канонической формы имеет размерность m × n и ранг m. Построим все m × m-подматрицы матрицы А0, отбрасывая вырожденные, оставшиеся подматрицы соответствуют базисам матрицы А0. Выберем из них допустимые базисы, построим соответствующие БДР. Выберем БДР, которое доставляет максимум целевой функции.
Но такой алгоритм на практике не может быть реализован, так как число БДР экспоненциально растет с ростом размерности задачи (числа переменных и/или ограничений). Процедуру можно ускорить, если организовать ее так, чтобы в процессе перебора БДР значение ЦФ не убывало (последовательное улучшение плана). Эта исходная идея симплекс-метода, которая реализуется следующим образом.
Симплекс-таблицы
Преобразования задачи ЛП в канонической форме, осуществляемые симплекс-методом, удобно представлять как преобразования симплекс-таблиц. Общий вид симплекс-таблицы, которая соответствует текущей итерации симплекс-метода, представляет таблица 1.
В верхней строке записаны: заголовок первого столбца, идентификаторы всех (основных, дополнительных, вспомогательных и др.) переменных задачи и заголовок последнего столбца. Следующие m строк описывают уравнения задачи в виде:
11 
(11)
который они имеют к началу итерации. Сначала указан идентификатор базисной переменной (в текущем базисе) для соответствующего уравнения. Затем следуют коэффициенты при переменных (в том порядке, в котором переменные записаны в первой строке). Последний элемент строки - правая часть ограничения.
Нижняя строка соответствует уравнению
12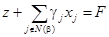 
, где 
и 
. (12)
представляющему ЦФ. Переменная z играет в нем роль базисной (имеет коэффициент 1 и не входит в другие уравнения); число F - это правая часть уравнения (12), значение ЦФ на текущем базисном решении.
Таблица 1. Общий вид симплекс-таблицы
| Базис | x1 | … | xs | … | xj | … | xn | Решение |
xj(1) 
(r)
(i)
(m)a11
…a1s…a1j…a1nb1
|
| ||||||||
|
|
… ars
ais…arj
…arnbr
| bi |
| …
| ||||||||
| … | … | aij | ain |
…
ams
…
amj
…
amn 
| bm | ||||||||
| z | g1 | … | gs | … | gj | … | gn | F |
Замечание. Таблица описывает систему уравнений (11), поэтому текущее БДР можно получить, полагая базисные переменные равными соответствующим элементам последнего столбца, а небазисные - равными нулю.
На рассматриваемой итерации происходит следующее.
Если в z-строке, в столбцах, соответствующих переменным, нет отрицательных элементов, то текущее БДР оптимально и в первом столбце таблицы записаны переменные оптимального базиса. В противном случае столбец переменной xs, для которого gs < 0, становится направляющим.
Если все элементы направляющего столбца неположительны, то задача неограниченна. В противном случае вычисляем отношение элементов последнего и направляющего столбцов для всех строк, имеющих положительный элемент в направляющем столбце. Строка r, для которой это отношение минимально, становится направляющей. В первом столбце следующей симплекс-таблицы переменная xs займет место переменной xj(r).
Теперь ars - разрешающий элемент. Элементы следующей симплекс-таблицы вычисляем по формулам:
13 
при 
при i ¹ r (13)
14 
(14)
15 
(15)
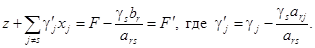16 
(16)
Рассмотрим j = j(k). Из (11) и (12) следует, что столбец j (базисный) имеет единицу в строке k и нули в остальных строках: gj = 0, aij = 1 при i = k, иначе aij = 0. Пусть k ¹ r (столбец j сохраняется в новом базисе). Тогда ari = 0 и из (13), (14), (16) следует, что 
для всех i и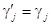 
. Учитывая это, сформулируем правила преобразования симплекс-таблицы при переходе к новому базису:
· в заголовок направляющей строки ставим заголовок направляющего столбца;
· все числа направляющей строки делим на разрешающий элемент;
· направляющий столбец становится единичным, с единицей в направляющей строке;
· столбцы текущего базиса с номерами, отличными от j(r), не изменяются;
· все остальные числа таблицы (включая элементы нижней строки и последнего столбца) пересчитываем по формулам (13) - (15), (16).
ПРИМЕНЕНИЕ СИМПЛЕКС-МЕТОДА ДЛЯ СОСТАВЛЕНИЯ ПЛАНА ПРОИЗВОДСТВА (НА ПРИМЕРЕ НЭРЗ)