Использование комбинаторики для подсчёта вероятностей








Ответ: а) 330; б) 24; в) 7920.
Произведение событий. Вероятность суммы двух событий.
Независимость событий.



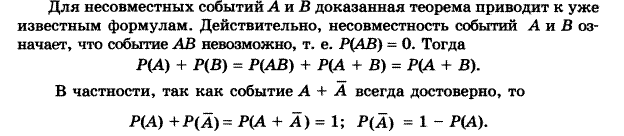






Решение задач по теории вероятностей
Примеры решения задач на тему: классическое определение вероятности
При решении задач с кубиками число всех возможных исходов можно посчитать по формуле п=6ª, где α –количество бросков
1. Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет нечетное число очков.
Решение. При бросании кубика равновозможных шесть различных исходов. Событию "выпадет нечётное число очков" удовлетворяют три случая: когда на кубике выпадает 1, 3 или 5 очков. Поэтому вероятность того, что на кубике выпадет нечётное число очков равна 3:6=0,5.
Ответ: 0,5.
2. Определите вероятность того, что при бросании кубика выпало число очков, не большее 3.
Решение. При бросании кубика равновозможны шесть различных исходов. Событию "выпадет не больше трёх очков" удовлетворяют три случая: когда на кубике выпадает 1, 2, или 3 очка. Поэтому вероятность того, что на кубике выпадет не больше трёх очков равна 3:6=0,5
Ответ: 0,5.
3. Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, большее 3.
Решение. При бросании кубика 6²= 36 различных исходов. Событию "выпадет больше трёх очков" удовлетворяют три случая: когда на кубике выпадает 4, 5, или 6 очков, благоприятных исходов 9 (4,4; 4,5; 4,6; 5,4; 5,5; 5,6; 6,4; 6,5; 6,6.)
Ответ: 9: 36 = 0,25.
4. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.
Решение. При бросании кубика 6³= 216 различных исходов, благоприятных 14. 14: 216 = 0,07.
Ответ: 0,07.
5. Коля выбирает трехзначное число. Найдите вероятность того, что оно делится на 5.
Решение. Всего трехзначных чисел 900. На пять делится каждое пятое их них, то есть таких чисел 900:5=180. Вероятность того, что Коля выбрал трехзначное число, делящееся на 5, определяется отношением количества трехзначных чисел, делящихся на 5, ко всему количеству трехзначных чисел: 180:900=0,2.
Ответ: 0,2.
6. Для экзамена подготовили билеты с номерами от 1 до 50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер?
Решение. Всего было подготовлено 50 билетов. Среди них 9 были однозначными. Таким образом, вероятность того, что наугад взятый учеником билет имеет однозначный номер, равна 9:50=0,18.
Ответ: 0,18.
7. В мешке содержатся жетоны с номерами от 5 до 54 включительно. Какова вероятность, того, что извлеченный наугад из мешка жетон содержит двузначное число?
Решение. Всего в мешке жетонов - 50. Среди них 45 имеют двузначный номер. Таким образом, вероятность, того, что извлеченный наугад из мешка жетон содержит двузначное число равна 45: 50 = 0,9.
Ответ: 0.9.
Противоположные события.
Событие, которое наступает в том и только в том случае, когла не наступает интересующее нас событие, называется противоположным данному событию. Сумма противоположных событий равна 1.
1. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,19. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Решение. Вероятность того, что ручка пишет хорошо, равна 1 − 0,19 = 0,81.
Ответ: 0,81.
2. Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже 36,8°C, равна 0,87. Найдите вероятность того, что в случайный момент времени у здорового человека температура тела окажется 36,8°C или выше.
Ответ. 1-0,87=0,13
3. При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм.
Решение. По условию, диаметр подшипника будет лежать в пределах от 66,99 до 67,01 мм с вероятностью 0,965. Поэтому искомая вероятность противоположного события равна 1 − 0,965 = 0,035.
Ответ: 0,035.