Как уже отмечалось, алгоритм обратного распространения ошибки был предложен в 1986 г. рядом авторов независимо друг от друга. Он является эффективным средством обучения нейронных сетей и представляет собой следующую последовательность шагов:
1. Задается шаг обучения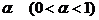 
и желаемая среднеквадратичная ошибка нейронной сети 
.
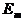2. Случайным образом инициализируются весовые коэффициенты и пороговые значения нейронной сети.
3. Последовательно подаются образы из обучающей выборки на вход нейронной сети. При этом для каждого входного образа выполняются следующие действия:
a) производится фаза прямого распространения входного образа по нейронной сети. При этом вычисляется выходная активность всех нейронных элементов сети:
,
где индекс j характеризует нейроны следующего слоя по отношению к слою i.
b) производится фаза обратного распространения сигнала, в результате которой определяется ошибка 
нейронных элементов для всех слоев сети. При этом соответственно для выходного и скрытого слоев:
,
.
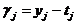В последнем выражении индекс i характеризует нейронные элементы следующего слоя по отношению к слою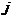 
.
c) для каждого слоя нейронной сети происходит изменение весовых коэффициентов и порогов нейронных элементов:
.
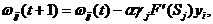
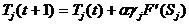4. Вычисляется суммарная среднеквадратичная ошибка нейронной сети:
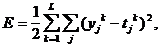
где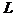 
— размерность обучающей выборки.
5. Если 
то происходит переход к шагу 3 алгоритма. В противном случае алгоритм обратного распространения ошибки заканчивается.
Таким образом, данный алгоритм функционирует до тех пор, пока суммарная среднеквадратичная ошибка сети не станет меньше заданной, т. е.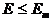 
.
Задание.
1. Написать на любом ЯВУ программу моделирования прогнозирующей нелинейной ИНС. Для тестирования использовать функцию
|
|
.
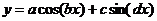Варианты заданий приведены в следующей таблице:
| № варианта | a | b | с | d | Кол-во входов ИНС | Кол-во НЭ в скрытом слое |
| 0.1 | 0.1 | 0.05 | 0.1 | |||
| 0.2 | 0.2 | 0.06 | 0.2 | |||
| 0.3 | 0.3 | 0.07 | 0.3 | |||
| 0.4 | 0.4 | 0.08 | 0.4 | |||
| 0.1 | 0.5 | 0.09 | 0.5 | |||
| 0.2 | 0.6 | 0.05 | 0.6 | |||
| 0.3 | 0.1 | 0.06 | 0.1 | |||
| 0.4 | 0.2 | 0.07 | 0.2 | |||
| 0.1 | 0.3 | 0.08 | 0.3 | |||
| 0.2 | 0.4 | 0.09 | 0.4 | |||
| 0.3 | 0.5 | 0.05 | 0.5 |
Для прогнозирования использовать многослойную ИНС с одним скрытым слоем. В качестве функций активации для скрытого слоя использовать сигмоидную функцию, для выходного - линейную.
2. Результаты представить в виде отчета содержащего:
1. Титульный лист,
2. Цель работы,
3. Задание,
4. График прогнозируемой функции на участке обучения,
5. Результаты обучения: таблицу со столбцами: эталонное значение, полученное значение, отклонение; график изменения ошибки в зависимости от итерации.
6. Результаты прогнозирования: таблицу со столбцами: эталонное значение, полученное значение, отклонение.
7. Выводы по лабораторной работе.
Результаты для пунктов 3 и 4 приводятся для значения a, при котором достигается минимальная ошибка. В выводах анализируются все полученные результаты.
Контрольные вопросы.
1. ИНС какой архитектуры Вы использовали в данной работе? Опишите принцип построения этой ИНС.
2. Как функционирует используема Вами ИНС?
3. Опишите (в общих чертах) алгоритм обучения Вашей ИНС.
|
|
4. Как формируется обучающая выборка для решения задачи прогнозирования?
5. Как выполняется многошаговое прогнозирование временного ряда?
6. Предложите критерий оценки качества результатов прогноза.