Показатели безотказности невосстанавливаемых объектов и методы их вычисления.

Одним из распространенных показателей надежности является ве­роятность безотказной работы (функция надежности) - вероятность того, что в пределах заданной наработки Т отказ объекта не возникает

где tо - наработка до отказа.

Статистически вероятность безотказной работы

где N - общее число наблюдаемых объектов; n(t) - число объектов, отказавших за время t от начала эксплуатации.

Наработка продолжительность или объем работы. Для контактов электромагнитных реле, например, объем работы измеряет­ся количеством замыканий при определенных токе и натяжении.

Вероятность появления отказа (функция ненадежности) Q(t) - ве­роятность того, что случайная величина времени наработки до первого от­каза будет меньше заданной наработки Т.

Для любого времени t по формуле полной вероятности

(1.3)

Очевидно, что При этом Q(t) монотонно возрастает, a P(t) монотонно убывает.

Частота отказов (плотность распределения отказов) - плотность ве­роятности того, что время работы объекта до отказа окажется меньше Т (плотность вероятности отказа к моменту времени Т), т.е.

(плотность вероятности отказа к моменту времени Т), т.е.

 

Статистическая оценка частоты отказов

 

 

где n(t) - число отказов к моменту времени t;

- число отказов на интервале времени от 0 до t + At;

- число отказов на интервале А/, примыкающем к t;

- число изделий, поставленных на испытание или пущенных в эксплуатацию;

- число работоспособных изделий к моменту t; - число работоспособных изделий по окончании интервала

Следовательно, - отношение числа отказов в интервале времени к произведению числа работоспособных объектов в начальный момент времени t =0 на длительность интервала времени

интенсивность отказов X(t) - условная вероятность того, что в интервале At произойдет отказ невосстанавливаемого объекта в единицу времени при условии, что до момента t отказ не произошел.

По определению при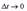

(1.6)

Статистическая оценка

(1.7)

где - число исправно работающих изделий в интервале At (1.8)

Для высоконадежных систем при 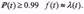Величина

ошибки при этом не более 1% и, как правило, не превышает ошибок ста­тистического определения величин Интегрируя выражение (1.6) с учетом (1.4) при начальном условии Р(0)=1 и С=0, получим

или (1.9)

В частном случае при Л = const формула (1.9) существенно упрощается:

(1.10)

экспоненциальный закон на­дежности (экспоненциальное распределение времени безотказной рабо­ты). Опыт работы систем радиоэлектроники, автоматики и телемеханики показывает, что интенсивность отказов в течение времени изменяется так, как показано на рис. 1.1. График функции можно разделить на три участка. На первом участке интенсивность отказов высока и уменьшается с течением времени. На этом участке выявляются скрытые дефек­ты производства аппаратуры, строительства и монтажа систем. Участок носит название участка приработки, и длительность его для устройств ра­диоэлектроники составляет десятки или сотни часов, а для электрической централизации

- от одного до четырех месяцев.

Второй участок - участок нормальной эксплуатации, характерен постоянным значением интенсивности отказов. Здесь проявляются
главным образом внезапные отказы. Длительность участка составляет ты­сячи и десятки тысяч часов.

На третьем участ­ке проявляется усиление старения эле­ментов, и интенсивность отказов начинает воз­растать. При достиже­нии времени аппара­ тура должна сниматься с эксплуатации.

Средняя наработка до отказа (среднее время безотказной работы) т математическое ожидание наработки до первого отказа

(1.11)

Для экспоненциального закона распределения времени безотказной работы

(1.12) Статистическая оценка средней наработки до отказа

(1.13)

где - время безотказной работы /-го изделия.

Гамма-процентная наработка до отказа - наработка, в течение

которой первый отказ объекта не возникает с заданной вероятностью
процентов.

 

 

5. Показатели безотказности восстанавливаемых объектов и методы их вычисления.

Для восстанавли­ваемых объектов харак­терно чередование работо­способного состояния и: восстановления работоспособности после отказа, т.е. процесс их эксплуатации можно представить (рис. 1.2) как последовательное чередование интервалов времени работоспособного и нерабо­тоспособного состояний (времени восстановления).

Появление отказов можно рассматривать как поток отказов или по­ток требований для восстановления. Основной характеристикой потека отказов является параметр потока отказов - плотность вероятности

возникновения отказа восстанавливаемого объекта в рассматриваемый момент времени (математическое ожидание числа отказов объекта, про­изошедших в единицу времени, начиная с момента t).

В теории надежности широко применяется простейший поток со следующими свойствами: 1) стационарностью, когда вероятность появ­ления п отказов в промежутке времени зависит только от п и 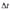и не зависит от положения промежутка на оси времени: 2) отсутствием по­следействия, когда вероятность наступления п отказов в течение проме­жутка времени не зависит от того, сколько было отказов и как они рас­пределялись до момента начала промежутка ; 3) ординарностью, когда появление в один и тот же момент времени более одного отказа невоз­можно.

Устройства железнодорожной автоматики и телемеханики являются восстанавливаемыми. После появления внезапного или постепенного от­каза отказавший элемент заменяется на новый, и эксплуатация устройства продолжается. В таком случае средняя частота отказов стремится к посто­янному значению [6], что характеризует стационарность потока отказов.

Свойство ординарности для отдельной схемы или отдельного эле­мента очевидно, но поток отказов в рассматриваемых системах является потоком с ограниченным последействием. Однако при достаточно боль­шом количестве элементов в системе и малой интенсивности их отказов, что присуще системам железнодорожной автоматики и телемеханики, по­ток отказов стремится к простейшему.

Таким образом, в системах железнодорожной автоматики и телеме­ханики соблюдаются необходимые и достаточные условия существования простейшего потока отказов как для внезапных, так и для постепенных от­казов. Это позволяет при оценке надежности отдельного элемента исполь­зовать экспоненциальный закон надежности.

Для ординарных потоков математическое ожидание числа отказов (1.14)

Для экспоненциального закона надежности

(1.15).

т.е. в системах жат понятия интенсивность отказов и параметр потока отказов можно не разделять Статистическая оценка параметра потока отказов

(1.16)

где - число изделий, отказавших в интервале времени

при условии, что отказавшее изделие немедленно за­меняется новым.

Средняя наработка на отказ - среднее время от окончания вос­становления работоспособности объекта после отказа до возникновения следующего отказа

(1.17)

Гамма-процентная наработка между отказами - средняя нара­ботка, в течение которой отказ восстанавливаемого объекта возникает с заданной вероятностью процентов.

Значение вероятности у всех объектов ЖАТ должно составлять минимально 90%.

Функциональная связь между показателями надежности

 

6.Показателем ремонтопригодности является вероятность восста­новления аботоспособности

- вероятность того, что время восста­новления работоспособности объекта не превысит заданного.

Время, затрачиваемое на обнаружение и устранение отказов, являет­ся случайной величиной, зависящей от ряда факторов: квалификации об­служивающего персонала, качества применяемых методов и средств поис­ка отказа, наличия специальных встроенных контрольных устройств и т.д.

Среднее время восстановления - математическое ожидание случайной продолжительности времени восстановления работоспособно­сти. По статистическим данным

(1.18)

где - длительность к-го восстановления;

п - общее число зафиксированных восстановлений. Интенсивность восстановления

Для устройств ЖАТ время восстановления включает в себя [30]: время фиксации отказа, время извещения электромеханика об отказе (5-10 мин.), время следования ремонтных работников к месту отказа (колеблется весьма широко в зависимости от расстояния до места отказа и используе­мых транспортных средств), время поиска места отказа (5-20-30 мин.), время устранения отказа (5-20-30 мин.), Время на опробование о оформление записей (5-10 мин.).

 

Комплексные показатели

Оценить в комплексе безотказность и ремон­топригодность позволяют комплексные показатели.

Коэффициент готовности К_г - вероятность того, что объект, нахо­дящийся в установившемся процессе эксплуатации, окажется работоспо­собным в произвольно выбранный момент времени, кроме планируемых периодов, в течение которых объект по назначению не применяется.

Статистическая оценка (1-20)

где - суммарное время нахождения изделия в работоспособном состоянии;

- суммарное время восстановления изделия.

Учитывая, что , где n - число отказов на интервале времени, для которого определяются значения , формулу

(1.20) можно записать в следующем виде:

(1.21)

Для непрерывно работающих систем, к которым относятся многие устройства железнодорожной автоматики и телемеханики, коэффициент готовности можно вычислять по следующей формуле:

(1-22) ^:

где Т_к - календарное время работы объекта, в течение которого зафик­сировано суммарное время восстановления

Обычно в расчетах высоконадежных объектов, к каким относятся системы ЖАТ, время Г_к выбирают продолжительностью в один год, или в часах - 8760 ч.

Коэффициент простоя К_п - вероятность того, что объект, находя­щийся в установившемся процессе эксплуатации, в произвольно выбран­ный момент времени будет в состоянии отказа (восстановления)

(1.23)

Коэффициент простоя используется, например, для нормирования надежности систем микропроцессорной централизации стрелок и сигналов (МПЦ) как по защитным, так и по опасным отказам (см. табл. 1.3).