Определение вероятности безотказной работы k – го элемента в указанный период времени

ПЕРМСИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ГОРНО-НЕФТЯНОЙ ФАКУЛЬТЕТ

КАФЕДРА ГЕОЛОГИИ НЕФТИ И ГАЗА

КОНТРОЛЬНАЯ РАБОТА

ПО ДИСЦИПЛИНЕ «ОСНОВЫТЕОРИИ НАДЕЖНОСТИ»

Вариант - №5,3,8

 

 

Выполнила студентка

заочного отделения

группы РНГМ-11-1у

______________/Гнездилова А.Н./

 

Проверил

________________/Никитин С.П../

 

Пермь 2014

Введение

Теория надёжности отражает общие закономерности, свойственные элементам и системам автоматики и телемеханики, которые необходимо учитывать при проектировании, изготовлении, испытаниях, приёмке и эксплуатации, чтобы достигнуть максимальной эффективности их использования. Повышение надёжности работы устройств автоматики и телемеханики является одной из важных задач обеспечения высокого качества технологического процесса и повышения безопасности движения поездов.

Методы теории надёжности позволяют:

1. выяснить характер действия окружающей среды и режимов работы на качество функционирования элементов и устройств,

2. разрабатывать способы анализа надёжности, необходимые для конструирования, проектирования и изготовления элементов, систем, прогнозирования неисправностей, их устранения, определения количества запасных деталей, приборов, механизмов и т.д.,

3. организовывать сбор, учет и анализ статистических сведений о работе элементов и эксплуатации,

4. определять наилучшие показатели надёжности,

5. определять способы лабораторных испытаний на надёжность и долговечность,

6. устанавливать наилучшие режимы профилактических работ и способы контроля качества работы элементов.

Формулировка понятий

Надёжность элементов (систем) – совокупность их свойств, определяющих степень возможности этих элементов (систем) работать по назначению в течение заданного времени.

Безотказность в работе – способность элемента (системы) сохранять работоспособность (не иметь отказов) в течение заданного времени в определённых условиях эксплуатации.

Долговечность элементов (систем) – способность к длительной эксплуатации в заданных условиях (при необходимом техническом обслуживании) вплоть до полного разрушения или другого предельного состояния.

Ремонтопригодность – свойство приспособленности к предупреждению, обнаружению и устранению неисправностей или к восстановлению после появления отказа.

Сохраняемость - свойство объекта сохранять в заданных пределах значения параметров, характеризующих способности объекта выполнять заданные функции, в течение и после хранения и (или) транспортирования.

Отказ – событие, заключающееся в нарушении работоспособного состояния объекта.

Ресурсный отказ – отказ, в результате которого объект достигает предельного состояния.

Независимый отказ - отказ, не обусловленный другими отказами.

Зависимый отказ – Отказ, обусловленный другими отказами (ГОСТ 27.002 – 89). Зависимый отказ наступает при отказе других элементов, входящих в данную систему или влияющих на отказавший элемент, или отказе собственных составных частей изделия.

Срок службы – календарная продолжительность эксплуатации от начала эксплуатации объекта или её возобновления после ремонта до перехода в предельное состояние.

Наработка до отказа – наработка объекта от начала эксплуатации до возникновения первого отказа.

Показатели надёжности

Вероятность безотказной работы – отношение числа элементов, оставшихся исправными в конце рассматриваемого интервала времени, к начальному числу элементов, поставленных на испытание:

;

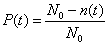где: N₀ – число изделий до начала эксплуатации

n(t) – число изделий, отказавших за промежуток времени

Физический смысл этой величины – способность элемента или системы выполнять заданные функции, сохранять параметры в определённых пределах в течение заданного промежутка времени и при определённых условиях эксплуатации.

Вероятность отказа – обратное событие, то есть вероятность того, что при определённых условиях и в заданном интервале времени наступит хотя бы один отказ:

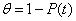
Частота отказов – отношение числа изделий, отказавших за определённый промежуток времени, к общему числу элементов системы:

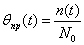
Интенсивность отказов - отношение числа изделий, отказавших за определённый промежуток времени, к среднему числу изделий, работающих исправно в данный промежуток времени:

;

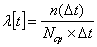
где:

N_cр – число исправно работающих изделий за время Δt

;

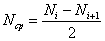надежность автоматика микросхема

где:

N_i , N_i+1 – число изделий, исправно работающих в начале и в конце интервала времени Δt

Наработка на отказ – среднее число часов работы между двумя соседними отказами:

;

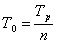Т_р – суммарное время работы за определённый календарный срок.

;

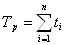где: t_i – время исправной работы между 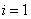и отказами

Среднее время восстановления – отношение времени, затраченного на обнаружение и устранение отказов, к числу восстановлений (оно же число отказов).

;

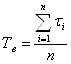где: τ_i – время от обнаружения до устранения отказа (время восстановления).

Коэффициент готовности – вероятность того, что восстанавливаемое изделие будет работоспособно в произвольный момент времени, кроме планируемых периодов, например, профилактика.

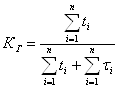или ;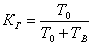

где: числитель – время исправной работы между отказами,

знаменатель – время исправной работы между отказами и время восстановления.

Коэффициент технического использования характеризует долю времени нахождения объекта в работоспособном состоянии относительно общей продолжительности эксплуатации.

;

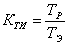Коэффициент простоя характеризует долю времени нахождения объекта в неисправном состоянии относительно общей продолжительности эксплуатации.

;

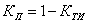Коэффициент ремонтопригодности – доля времени восстановления относительно общей продолжительности эксплуатации.

;

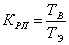Коэффициент стоимости эксплуатации определяется как отношение среднего суммарного эффекта за время эксплуатации к средним суммарным затратам.

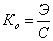
Средний суммарный эффект Э складывается из эффекта от эксплуатации устройства, умноженного на показатель надёжности устройства и время эксплуатации.

Средние суммарные затраты определяются как функция от суммарных затрат на техническое обслуживание, функция от суммарного ущерба вследствие отказа устройства и функция от произведения показателя надёжности на время эксплуатации.

1. Метод Каплана - Майера

На испытание было поставлено N = 56 элементов. Моменты отказов элементов представлены в табл.1. Все элементы работали до своего отказа и после отказа не ремонтировались.

1. Необходимо по данным экспериментам построить график изменения вероятности безотказной работы.

Для оценки вероятности безотказной работы 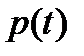системы по экспериментальным данным используем метод Каплана-Майера

;

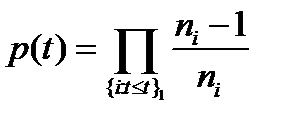Где 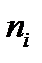- число изделий, оставшихся в работоспособном состоянии на момент времени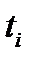

 

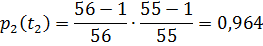
Остальные значения рассчитываем аналогично и заносим в таблицу 1

Таблица 1

i	ti	(ni-1)/n1	Pi(ti)	i	ti	(ni-1)/n1	Pi(ti)
	0,8343	0,982	0,982		38.99	0,964	0,482
	0,8844	0,982	0,964		42,14	0,963	0,464
	2,037	0,981	0,946		43,20	0,962	0,446
	2,650	0,981	0,928		43,59	0,960	0,429
	3,208	0,981	0,910		47,34	0,958	0,411
	5,266	0,980	0,892		49,62	0,957	0,393
	5,883	0,980	0,874		58,41	0,955	0,375
	6,693	0,980	0,856		60,10	0,952	0,357
	7,478	0,979	0,838		65,02	0,950	0,339
	7,863	0,979	0,821		71,24	0,947	0,321
	10,89	0,978	0,803		74,86	0,944	0,304
	10,91	0,978	0,785		76,70	0,941	0,286
	11,38	0,977	0,767		77,78	0,938	0,268
	14,04	0,978	0,750		81,92	0,933	0,250
	14,18	0,976	0,732		82,76	0,929	0,232
	15,94	0,976	0,714		92,22	0,923	0,214
	18,27	0,975	0,696		93,08	0,917	0,196
	19,46	0,974	0,679		104,1	0,909	0,179
	20,14	0,974	0,661		106,5	0,900	0,161
	21,22	0,973	0,643		109,6	0,889	0,143
	21,86	0,972	0,625		113,0	0,875	0,125
	22,38	0,971	0,607		131,0	0,857	0,107
	22,47	0,971	0,589		146,0	0,833	0,089
	22,95	0,970	0,571		178,1	0,800	0,071
	25,61	0,969	0,554		194,8	0,750	0,054
	26,94	0,968	0,536		227,4	0,667	0,036
	29,15	0,967	0,518		255,2	0,500	0,018
	35,39	0,966	0,500		278,2	0,000	0,000

 

 

По данным таблицы строим график изменения вероятности безотказной работы системы (рис.1)

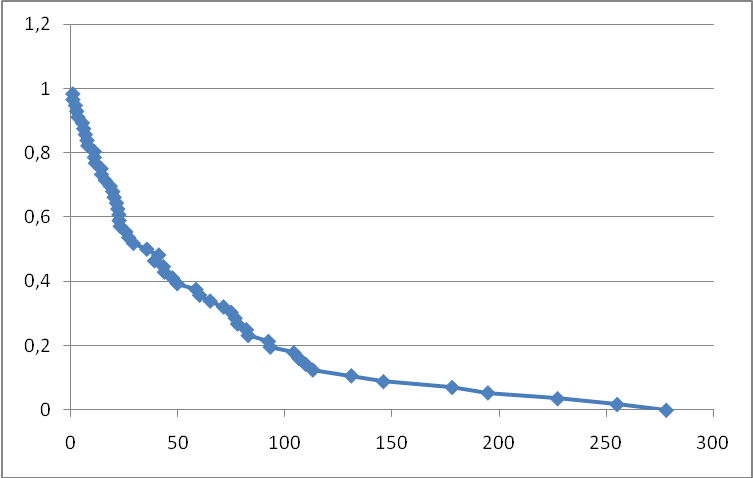
Рис. 1. Вероятность безотказной работы системы

Ответ: На основание Рис.1 принимаем экспоненциальное распределение

Построение гистограммы.

На испытания было поставлено 56 элементов. Моменты отказов элементов представлены в таблице. Все элементы работали до своего отказа и после отказа не ремонтировались

Построим дискретный вариационный ряд. Для этого отсортируем ряд по возрастанию и подсчитаем количество повторения для каждого элемента ряда.

Число групп приближенно определяется по формуле Стэрджесса

n = 1 + 3,2log n

n = 1 + 3,2log(56) = 7

Решение.

Ширина интервала составит:

 

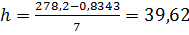
Xmax - максимальное значение группировочного признака в совокупности.

Xmin - минимальное значение группировочного признака.

Определим границы группы.

Таблица 2

Номер группы	Нижняя граница	Верхняя граница
1	0,8343	40,45
2	40,45	80,07
3	80,07	119,69
4	119,69	159,31
5	159,31	198,93
6	198,93	238,55
7	238,55	278,2

 

Одно и тоже значение признака служит верхней и нижней границами двух смежных (предыдущей и последующей) групп.

Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.

Таблица 3

 

0,8343	0,8343-40,45
0,8844	0,8343-40,45
2,037	0,8343-40,45
2,650	0,8343-40,45
3,208	0,8343-40,45
5,266	0,8343-40,45
5,883	0,8343-40,45
6,693	0,8343-40,45
7,478	0,8343-40,45
7,863	0,8343-40,45
10,89	0,8343-40,45
10,91	0,8343-40,45
11,38	0,8343-40,45
14,04	0,8343-40,45
14,18	0,8343-40,45
15,94	0,8343-40,45
18,27	0,8343-40,45
19,46	0,8343-40,45
20,14	0,8343-40,45
21,22	0,8343-40,45
21,86	0,8343-40,45
22,38	0,8343-40,45
22,47	0,8343-40,45
22,95	0,8343-40,45
25,61	0,8343-40,45
26,94	0,8343-40,45
29,15	0,8343-40,45
35,39	0,8343-40,45
38.99	0,8343-40,45
42,14	40,45-80,07
43,20	40,45-80,07
43,59	40,45-80,07
47,34	40,45-80,07
49,62	40,45-80,07
58,41	40,45-80,07
60,10	40,45-80,07
65,02	40,45-80,07
71,24	40,45-80,07
74,86	40,45-80,07
76,70	40,45-80,07
77,78	40,45-80,07
81,92	80,07-119,69
82,76	80,07-119,69
92,22	80,07-119,69
93,08	80,07-119,69
104,1	80,07-119,69
106,5	80,07-119,69
109,6	80,07-119,69
113,0	80,07-119,69
131,0	119,69-159,31
146,0	119,69-159,31
178,1	159,31-198,93
194,8	159,31-198,93
227,4	198,93-238,55
255,2	238,55-278,2
278,2	238,55-278,2

 

Результаты группировки оформим в виде таблицы:

 

 

Таблица 4

 

Группы	№ совокупности	Частота f i
0,8343-40,45	1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29
40,45-80,07	30,31,32,34,35,36,37,38,39,40,41,42
80,07-119,69	43,44,45,46,47,48,49,50
119,69-159,31	51,52
159,31-198,93	53,54
198,93-238,55
238,55-278,2	55,56

Гистограмма.

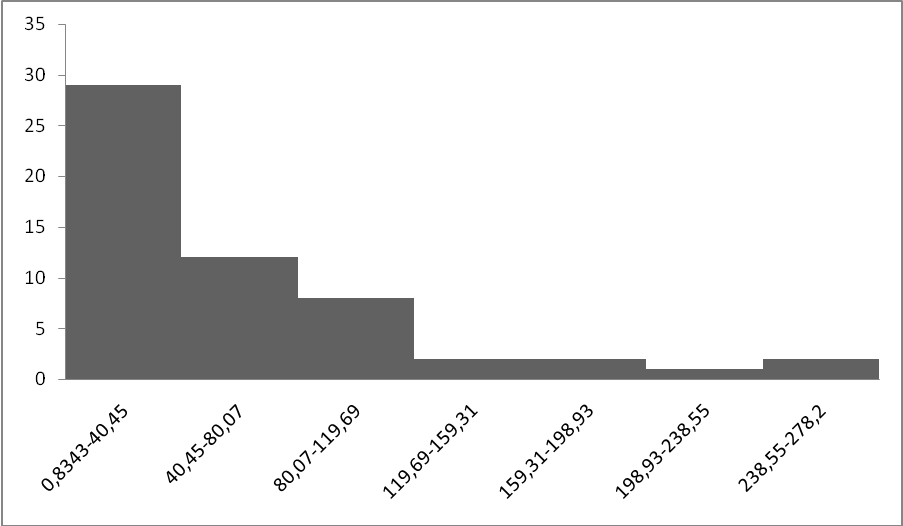
Рис. 2 Гистограмма

Вывод – наибольшее количество элементов выходящих из строя принадлежит интервалу 0.8343 – 40.45

Ответ: На основание Рис.2 принимаем экспоненциальное распределение

Метод Вейбулла

По данным эксперимента, используя вероятностную сетку Вейбулла, проверить тип распределения и определить параметры распределения.

Решение.

3.1. Определяем значение интегральной функции отказов устройств при испытании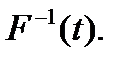

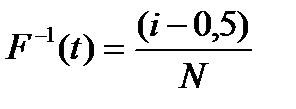
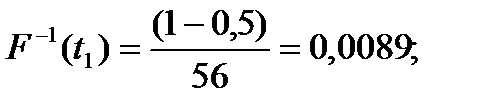
Остальные значения рассчитываем аналогично и заносим в таблицу 5

1	0,8343	0,0089
2	0,8844	0,0268
3	2,037	0,0446
4	2,650	0,0625
5	3,208	0,0804
6	5,266	0,0982
7	5,883	0,1161
8	6,693	0,1339
9	7,478	0,1518
10	7,863	0,1696
11	10,89	0,1875
12	10,91	0,2054
13	11,38	0,2232
14	14,04	0,2411
15	14,18	0,2589
16	15,94	0,2768
17	18,27	0,2946
18	19,46	0,3125
19	20,14	0,3304
20	21,22	0,3482
21	21,86	0,3661
22	22,38	0,3839
23	22,47	0,4018
24	22,95	0,4196
25	25,61	0,4375
26	26,94	0,4554
27	29,15	0,4732
28	35,39	0,4911
29	38.99	0,5089
30	0,963	0,5268
31	0,962	0,5446
32	0,960	0,5625
33	0,958	0,5804
34	0,957	0,5982
35	0,955	0,6161
36	0,952	0,6339
37	0,950	0,6518
38	0,947	0,6696
39	0,944	0,6875
40	0,941	0,7054
41	0,938	0,7232
42	0,933	0,7411
43	0,929	0,7589
44	92,22	0,7768
45	93,08	0,7946
46	104,1	0,8125
47	106,5	0,8304
48	109,6	0,8482
49	113,0	0,8661
50	131,0	0,8839
51	146,0	0,9018
52	178,1	0,9196
53	194,8	0,9375
54	227,4	0,9554
55	255,2	0,9732
56	278,2	0,9911

 

Наносим по данным таблицам экспериментальные точки на вероятностную сетку Вейбулла (рис.3), соединяем их полигоном, аппроксимируем точки прямой линией. С помощью полученной линии интегральной функции распределения определяем интенсивность отказов устройств и угол наклона прямой

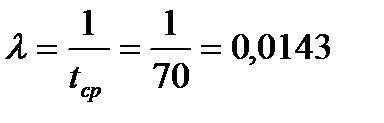
Где - берем с Рис.3.

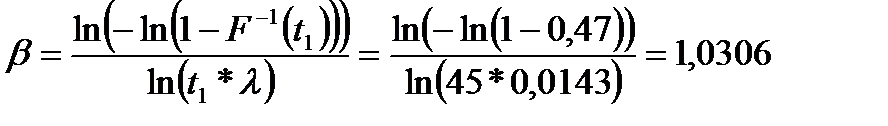
Где 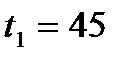- берем с Рис.3.

- соответствует значению 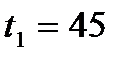(см. Рис.3)

Вывод – принимаем экспоненциальное распределение

30/33

Определение вероятности безотказной работы k – го элемента в указанный период времени

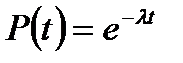
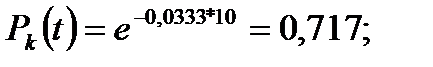
Вывод – интенсивность отказа 3 – го элемента 0,0333, вероятность отказа – 0,717.