ПРИМЕРЫРЕШЕНИЯ ЗАДАЧ
Пример 1. В таблице даны опытные данные адсорбции газа (адсорбата) на соответствующем адсорбенте:
V, м3/г - объем газа, адсорбированного 1 граммом адсорбента;
Р, Па - давление газа (адсорбата) над адсорбентом.
1. Построить изотерму адсорбции V = f(Р) - рис. 1.
2. Найти графически коэффициенты уравнения Лэнгмюра, записать полученное уравнение Лэнгмюра, вычислить значения адсорбции по полученному уравнению и построить расчетную кривую V = f(Р) на том же рис. 1.
| Т, К | Адсорбент | Адсорбат | Р´10- 3, Па | V´ 106, м3/г |
| 2,0 | 10,4 | |||
| 4,27 | 20,8 | |||
| Уголь | С2Н4 | 10,57 | 30,5 | |
| 29,5 | 42,4 | |||
| 91,5 | 55,2 |
Решение: 1) Построим изотерму адсорбции V = f (Р) по опытным данным (рис. 1, кривая 1, точки ·).
2) Уравнение Лэнгмюра для адсорбции газа записывается в виде:
(1)
где Г - количество газа-адсорбата, адсорбированное 1 г адсорбента (или 1 см3 его поверхности) в заданных условиях; Г¥ — максимальное количество газа-адсорбата, адсорбированное 1 г адсорбента (или 1 см3 его поверхности) в заданных условиях; Р - равновесное давление газа-адсорбата.
Количество газа-адсорбата удобно измерять в виде объема (V). Тогда уравнение (1) запишется в виде:
(2)
где V и V¥ имеют тот же смысл, что и Г и Г¥ в уравнении (1).
Коэффициентами уравнения Лэнгмюра являются V¥ и k. Чтобы графически найти эти коэффициенты, уравнение Лэнгмюра необходимо линеаризовать (привести к линейной форме):
(3)
Затем строится график зависимости 
и по графику полученной прямой линии находят коэффициенты V¥ и k. Зависимость предcтавлена на рис. 2 в соответствии с данными таблицы:
Данные для вычисления величины адсорбции С2Н4 на угле
по уравнениям (3, 5)
| 
| V´106, м3/г, вычисленный по уравнению (5) |
| 5,00 | 96,2 | 10,5 |
| 2,34 | 48,1 | 18,5 |
| 0,95 | 32,8 | 30,7 |
| 0,34 | 23,6 | 43,1 |
| 0,11 | 18,1 | 51,0 |
По представленному на рис. 2 графику прямой линии находим коэффициенты уравнения Лэнгмюра V¥ и k.
Из графика 
= 18,0. Отсюда V¥ = 55,55´10-6 м3/г.
Из графика tgα = 15,4´107, из уравнения (3) 
, следовательно,
Подставим найденные значения коэффициентов в уравнение (2) и запишем выражение для вычисления V = f (Р) по уравнению Лэнгмюра:
(4)
или
(5)
Вычислим V по уравнению (5), запишем полученные расчетные данные таблицу 1 и нанесем полученные точки в координатах V — Р на рис. 1 (кривая точки ▪).
Поскольку опытная кривая 1 и расчетная кривая 2 на рис. 1 совпадают, сделаем вывод о правильности найденных коэффициентов уравнения Лэнгмюра.
|
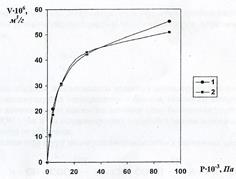
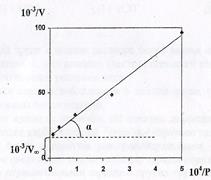
Рис. 1 Изотерма адсорбции V = f (Р) С2Н4 на угле при 293 К
кривая 1 (·) - опытные данные
кривая 2 (▪) - значения V = f (Р), найденные по уравнению Лэнгмюра (2, 5)
МНОГОВАРИАНТНЫЕ ЗАДАНИЯ
Задача 1. Найти графически коэффициенты Лэнгмюра, записать полученное уравнение Лэнгмюра, вычислить значения адсорбции по полученному уравнению и построить расчетную кривую V = f(Р) на том же рис.1.
| Вари-ант | Т, К | Адсорбент | Адсорбат | Р·10-3, Па | V·106, м3/г |
| 1, 16 | Уголь | N2 | 1,62 5,30 17,3 30,70 44,50 | 0,31 0,99 3,04 5,10 6,90 | |
| 2, 17 | Уголь | CO2 | 4,20 8,10 11,70 16,50 24,00 | 12,73 21,20 26,40 32,20 38,60 | |
| 3, 18 | Уголь | CO | 9,80 24,20 41,30 60,00 72,50 | 2,53 5,57 8,43 11,20 12,85 | |
| 4, 19 | Уголь | NH3 | 10,50 21,60 42,70 65,60 85,20 | 60,40 90,30 115,70 127,00 132,40 | |
| 5, 20 | BaF2 | CO | 11,30 24,40 44,50 61,00 82,50 | 2,04 3,72 5,30 6,34 7,30 | |
| 6, 21 | Уголь | H2 | 27,60 43,40 57,40 72,20 86,10 | 0,447 0,698 0,915 1,142 1,352 | |
| 7, 22 | 194,5 | Уголь | N2 | 1,67 8,83 20,00 36,30 52,00 | 3,47 13,83 23,00 27,94 33,43 |
| 8, 23 | 194,5 | Уголь | CH4 | 25,60 36,70 47,80 60,50 77,00 | 15,20 19,10 22,30 25,30 28,40 |
| 9, 24 | 194,5 | Уголь | CO | 4,00 5,34 9,65 16,65 19,80 | 15,80 19,05 27,70 34,10 38,95 |
| 194,5 | Уголь | Ar | 3,22 7,25 12,15 17,25 39,50 | 5,09 10,02 15,56 18,81 29,14 | |
| 194,5 | Уголь | CH4 | 25,60 36,70 47,80 60,50 77,00 | 15,2 19,1 22,3 25,3 28,4 | |
| 194,5 | Уголь | CO | 4,00 5,34 9,65 16,65 19,80 | 15,80 19,05 27,70 34,10 38,95 | |
| 194,5 | Уголь | Ar | 3,22 7,25 12,15 17,25 39,50 | 5,09 10,02 15,56 18,81 29,14 | |
| Уголь | C2H4 | 9,35 12,45 22,50 42,60 82,50 | 39,5 42,8 49,9 56,5 64,5 | ||
| Уголь | C2H4 | 2,00 4,27 10,57 29,5 91,5 | 10,4 20,8 30,5 42,4 55,2 |
Коллоидные растворы
Оптические свойства коллоидных растворов
ПРИМЕРЫРЕШЕНИЯ ЗАДАЧ
Пример 1. При исследовании гидрозоля серебра с помощью ультрамикроскопа в видимом объеме подсчитано 10 частиц. Площадь поля зрения составляет 4,5·10-8 м2, глубина пучка 8·10-6 м. Приняв форму частиц за шарообразную, вычислите их средний радиус. Массовая концентрация золя составляет 3·10-5 кг/м3, плотность серебра равна 10,5·103 кг/м3.
Решение: Одним из первых методов исследования коллоидных растворов, основанных на их опалесценции, является ультрамикроскопия. С помощью ультрамикроскопа Зигмонди можно подсчитать число частиц n в определенном объеме золя V (м3).
Формула для расчета среднего радиуса частиц r (шарообразная форма)
, м
где, ν – частичная концентрация (число частиц в 1 м3), V – объем каждой частицы (м3), С – массовая концентрация (масса частиц дисперсной фазы в 1 м3 золя), кг/м3, ρ – плотность частиц дисперсной фазы, кг/м3.
Длина ребра кубической частицы будет равна:
Т.к. объем раствора в поле зрения микроскопа равен произведению площади поля зрения микроскопа S на глубину пучка света h: V = S·h = 4,5·10-8·8·10-6 = 3,6·10-13 м3, то средний радиус частиц будет равен:
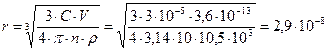м
МНОГОВАРИАНТНЫЕ ЗАДАНИЯ
Задача 1.
| Вари-ант | Задача |
| 1, 9, 17 | При исследовании гидрозоля золота с помощью ультрамикроскопа в видимом объеме v = 12·10-19 м3 подсчитано 5 частиц. Приняв форму частиц за шарообразную, рассчитать их средний радиус. Концентрация золя с = 30·10-2 кг/м3, плотность золота ρ = 19,3·103 кг/м3. |
| 2, 10, 18 | При ультрамикроскопическом исследовании гидрозоля серебра в кювете площадью 5,4·10-12 м2 и глубиной пучка света 2,5·10-4 м подсчитано 2 частицы. Рассчитайте среднюю длину ребра частицы, принимая их форму за кубическую. Массовая концентрация золя серебра равна 0,02 кг/м3, плотность серебра составляет 10,5·103 кг/м3. |
| 3, 11, 19 | При исследовании аэрозолей методом поточной ультрамикроскопии в объеме V = 1,33·10-11 м3, протекшем через счетное поле микроскопа, подсчитано 50 частиц масляного тумана. Определить средний радиус частиц, приняв их форму за сферическую. Весовая концентрация аэрозоля C = 25·10-6 кг/м3, плотность ρ = 0,9 ·103 кг/м3. |
| 4, 12, 20 | С помощью метода поточной ультрамикроскопии в прошедшем объеме V = 2·10-11 м3 подсчитано 100 частиц золя серы. Концентрация золя С = 6,5·10-5 кг/м3, плотность ρ = 1 ·103 кг/м3. Рассчитать средний радиус частиц, приняв их форму за сферическую. |
| 5, 13, 21 | При исследовании гидрозоля Fe2O3 с помощью ультрамикроскопа в видимом объеме 4·10-15 м3 было подсчитано 3 частицы. Принимая, что частицы золя сферические и плотность равна 5,2·103 кг/м3, определите средний радиус частиц гидрозоля. Массовая концентрация гидрозоля равна 8,5·10-4 кг/м3. |
| 6, 14, 22 | С помощью метода поточной ультрамикроскопии в объеме равном 2,2·10-11 м3 подсчитано 80 частиц дыма мартеновских печей. Массовая концентрация аэрозоля равна 1·10-4 кг/м3, плотность составляет 2·103 кг/м3. Рассчитайте среднюю длину ребра частицы, принимая их форму за кубическую. |
| 7, 15, 23 | Методом поточной ультрамикроскопии в объеме 1,5·10-11 м3 подсчитано 53 частицы аэрозоля масляного тумана. Считая форму частиц сферической, определите их средний радиус. Массовая концентрация золя составляет 2,1·10-5 кг/м3, плотность равна 0,92·103 кг/м3. |
| 8, 16, 24 | Методом поточной ультрамикроскопии в объеме 3·10-11 м3 подсчитано 60 частиц аэрозоля водяного тумана. Каков средний радиус частиц, если массовая концентрация золя составляет 1,5·10-5 кг/м3, плотность равна 0,99·103 кг/м3. Форму частиц примите за сферическую. |
Задача 2. Используя экспериментальные значения оптической плотности D для разных длин волн λ, определить средний радиус частиц полистирольного латекса.
Примечание: 1) При построении логарифмической прямой целесообразно брать логарифм 100 D. 2) Предварительно построить калибровочную кривую Геллера по следующим данным.
| Диаметр частиц латекса d·109, м | 106,7 | |||||
| Характеристика дисперсности α | 3,85 | 3,64 | 3,545 | 3,3 | 3,235 | 3,04 |
Продолжение таблицы
| Диаметр частиц латекса d·109, м | ||||||
| Характеристика дисперсности α | 2,82 | 2,72 | 2,66 | 2,45 | 2,365 | 2,14 |
Экспериментальные данные для вариантов
| Варианты | Длина волны λ ·10-9, м | ||||
| 1,5,9,13, 17,21 | Оптическая плотность латекса D | 0,195 | 0,127 | 0,099 | 0,048 |
Экспериментальные данные для вариантов
| Варианты | Длина волны λ ·10-9, м | ||||
| 2,6,10,14, 18,22 | Оптическая плотность латекса D | 0,474 | 0,329 | 0,259 | 0,133 |
Экспериментальные данные для вариантов
| Варианты | Длина волны λ ·10-9, м | ||||
| 3,7,11,15, 19,23 | Оптическая плотность латекса D | 0,324 | 0,215 | 0,16 | 0,084 |
Экспериментальные данные для вариантов
| Варианты | Длина волны λ ·10-9, м | ||||
| 4,8,12,16, 20,24 | Оптическая плотность латекса D | 0,189 | 0,129 | 0,104 | 0,05 |