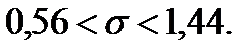Дисперсия
Определения
Пусть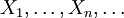 
- выборка из распределения вероятности. Тогда
· выборочная дисперсия - это случайная величина
Dв=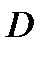 
= 
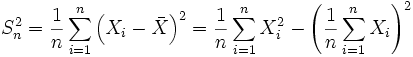, (1)
где символ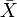 
обозначает выборочное среднее.
· Несмещённая (исправленная) дисперсия - это случайная величина
.
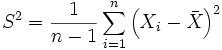Замечание
Очевидно,
.= 
.
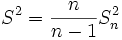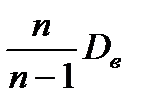Свойства выборочных дисперсий
· Выборочная дисперсия является смещённой оценкой теоретической дисперсии, а исправленная выборочная дисперсия несмещённая:
,
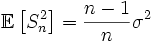и
.
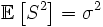Математическая статистика
Эмпирическая функция распределения
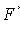
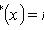
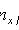
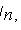
где nx - число выборочных значений, меньших x; n - объем выборки.
Выборочное среднее
(несмещенная, состоятельная оценка математического ожидания)
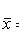
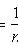
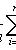
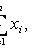
где xi - выборочные значения; n - объем выборки.
Выборочная дисперсия
(смещенная, состоятельная оценка дисперсии)
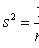
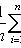
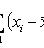
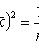
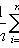
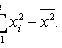
Исправленная выборочная дисперсия
(несмещенная, состоятельная оценка дисперсии)
Умный способ вычисления среднего и дисперсии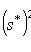 
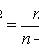
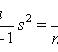
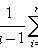
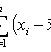
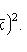
Если варианты xi, большие, то выбираем условное среднее с наибольшей частотой С и вводим новую случайную величину
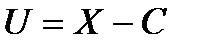
и вычисляем её среднее и дисперсию. Тогда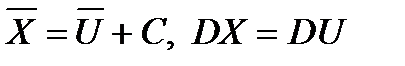 
.
Пример 1.
| Xi | |||||
| Ni |
C = 2620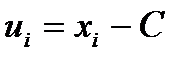 
| Ui | -60 | -20 |
.
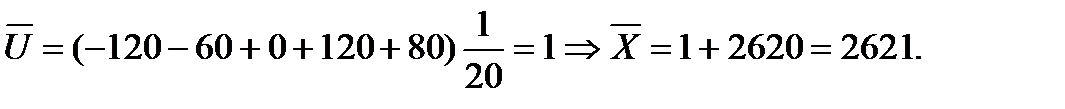
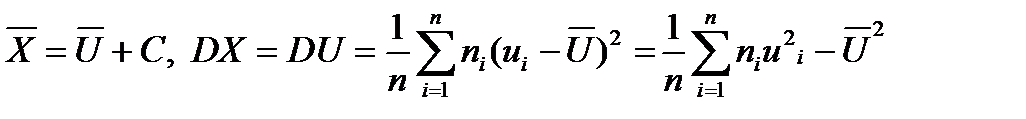
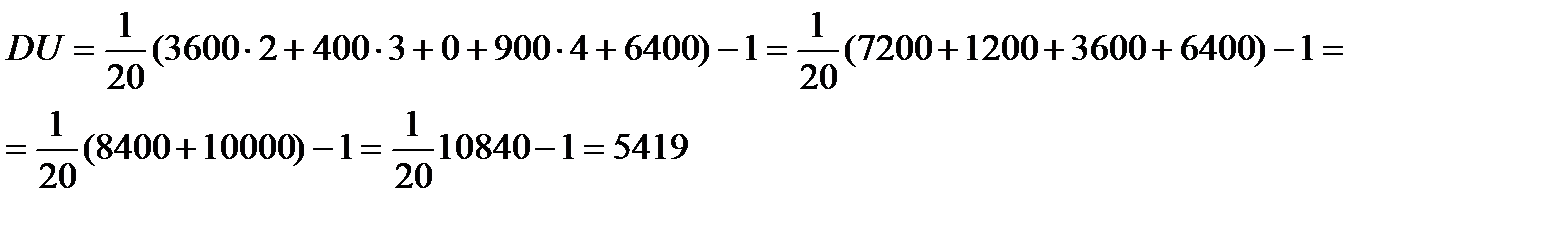Исправленная дисперсия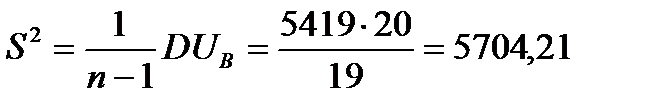 
.
Интервальные оценки и доверительный интервал
Интервальной называют оценку, которая определяется двумя числами – концами интервала. Интервальные оценки позволяют установить точность и надёжность оценок.
Итак, пусть, найденная по данным выборки, статистическая характеристика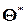 
служит оценкой неизвестного параметра 
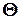. Будем считать 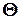постоянным числом ( 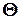может быть и случайной величиной). Ясно, что 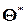тем точнее определяет параметр 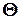, чем меньше абсолютная величина разности 
. Другими словами, есл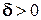и 
и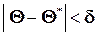 
, то, чем меньше 
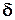, тем оценка точнее. Таким образом, положительное число 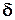характеризует точность оценки.
К сожалению статистические методы не позволяют категорически утверждать, что оценка 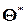удовлетворяет неравенству 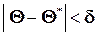; можно лишь говорить о вероятности 
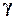, с которой это неравенство осуществляется.
Надёжностью (доверительной вероятностью) оценки 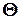по 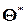называют вероятность 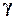, с которой осуществляется неравенство 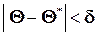, то есть
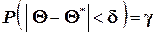
Обычно, надёжность оценки задаётся наперёд, причём в качестве 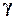берут число, близкое к единице. Выбор доверительной вероятности не является математической задачей, а определяется конкретной решаемой проблемой. Наиболее часто задают надёжность, равную 0,95; 0,99; 0,999.
Согласно определению
.
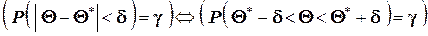Это соотношение следует понимать так: вероятность того, что интервал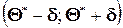 
заключает в себе (покрывает) неизвестный параметр 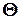равна .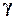
Доверительным называют интервал 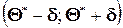, который покрывает неизвестный параметр с заданной надёжностью .
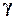Метод доверительных интервалов разработан американским статистиком Ю.Нейманом, исходя из идей английского статистика Р.Фишера.
Доверительный интервал для генеральной средней при известном значении среднего квадратического отклонения Ϭ и при условии, что случайная величина (количественный признак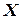 
) распределена нормально, задаётся выражением:
,
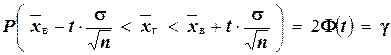где 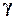– наперёд заданное число, близкое к единице, 
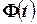– функция Лапласа, значения которой приведены в соответствующей таблице, 
.
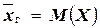Смысл полученного соотношения таков: с надёжностью 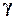можно утверждать, что доверительный интервал 
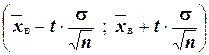покрывает неизвестный параметр 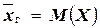при точности оценки 
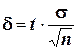. Заметим, что число 
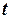определяется из равенства 
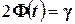, или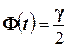 
; по таблице значений функции Лапласа находят аргумент 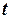, которому соответствует значение равное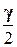 
Замечание: оценку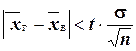 
называют классической. Из формулы 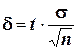, определяющей точность классической оценки, моно сделать следующие выводы:
- при возрастании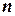 
– объёма выборки число 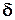убывает и, следовательно, точность оценки увеличивается;
- увеличение надёжности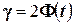 
приводит к увеличению 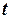(так как функция 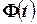является возрастающей), а следовательно, и к возрастанию 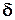. Другими словами, увеличение надёжности классической оценки влечёт за собой уменьшение её точности.
ПРИМЕР 1. Случайная величина 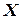имеет нормальное распределение с известным средним квадратическим отклонением 
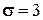. Найти доверительные интервалы для оценки неизвестного математического ожидания 
(или, что тоже самое, для оценки неизвестной генеральной средней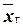 
) по выборочным средним 
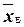, если объём выборки 
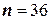и задана надёжность оценки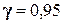 
Решение. Найдём, прежде всего, 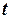. Из соотношения 
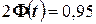получим 
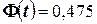. Далее, по таблице находим 
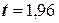. Теперь, найдём точность оценки:
.
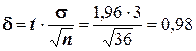Доверительные интервалы таковы: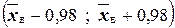 
. Например, если 
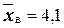, то доверительный интервал имеет следующие доверительные границы:
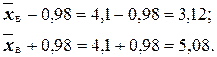
Таким образом, значения неизвестного параметра (или 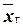), согласующиеся с данными выборки находятся в интервале 
.
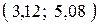Подчеркнём, что было бы ошибочным написать: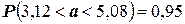 
. Действительно, так как – постоянная величина, то либо она заключена в найденном интервале (тогда событие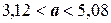 
достоверно и его вероятность равна единице), либо в нём не заключена (в этом случае событие 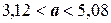невозможно и его вероятность равна нулю). Другими словами, доверительную вероятность не следует связывать с оцениваемым параметром; она связана лишь с границами доверительного интервала, которые, как уже было сказано, изменяются от выборки к выборке.
Поясним смысл, который имеет заданная надёжность. Надёжность 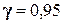указывает, что если произведено достаточно большое число выборок, то 95% из них определяет такие доверительные интервалы, в которых параметр (или 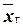) действительно заключён; лишь в 5% случаев он может выйти за границы доверительного интервала.
Замечание: если требуется оценить математическое ожидание (генеральную среднюю) с наперёд заданной точностью 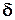и надёжностью 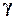, то минимальный объём выборки, который обеспечит эту точность, находят по формуле:
(как следствие равенства ).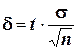
Доверительный интервал для генеральной средней 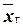(математического ожидания ) нормально распределённого признака при неизвестном значении среднего квадратического отклонения задаётся выражением:
,
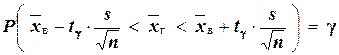где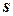 
– «исправленное» среднее квадратическое отклонение, параметр 
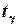находят по заданным значения 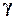и 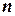из соответствующих таблиц Гмурман Приложение 3 (и наоборот, по заданным 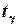и 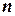находят вероятность 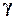). Отсюда следует, что с надёжностью 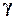можно утверждать, что доверительный интервал 
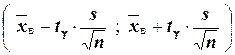покрывает неизвестный параметр .
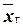ПРИМЕР 2. Количественный признак 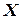генеральной совокупности распределён нормально. По выборке объёма 
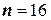найдены выборочная средняя 
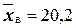и «исправленное» среднее квадратическое отклонение 
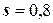. Оценить неизвестную генеральную среднюю 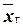с помощью доверительного интервала с надёжностью .
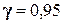Решение. Пользуясь таблицей (см. приложения), по известным значениям 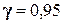и 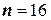находим 
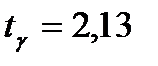. Тогда, доверительные границы:
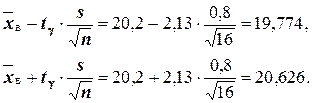
Итак, с надёжностью 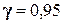неизвестный параметр 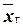, заключён в доверительном интервале 
.
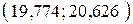2. Интервальной оценкой (с надежностью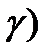 
среднего квадратического отклонения 
нормально распределенного количественного признака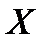 
по «исправленному» выборочному среднему квадратическому отклонению 
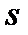служит доверительный интервал:
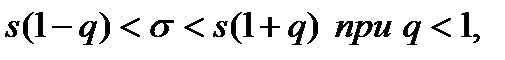
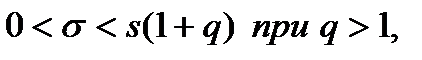
где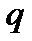 
находятся по таблице приложения 4 по заданным 
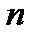и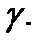 
Пример 3.58. По данным выборки объема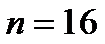 
из генеральной совокупности найдено «исправленное» выборочное среднее квадратическое отклонение S=1 нормально распределенного количественного признака X. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение с надежностью 0,95.
По данным задач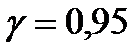и 
и 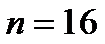в таблице приложения 4 найдем 
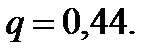Поскольку 
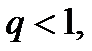то используя формулу (3.43) найдем искомый интервал 