Нижегородский государственный университет
Им. Н.И. Лобачевского
Экономический факультет
Кафедра экономической информатики
ЗАДАНИЯ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

Для студентов экономических специальностей.
Учебно-методическое пособие
Г.Н.Новгород
2005 г.
Задания к практическим занятиям по теории вероятностей для студентов экономических специальностей. – Учебное пособие.
Составитель: Е.Н. Вышинская – Н.Новгород. 2005 –
В учебном пособии даны задачи по всем основным темам курса теории вероятностей. Пособие обеспечивает методическую поддержку практических занятий по теории вероятностей для студентов второго курса, обучающихся на экономическом факультете. Приводится большое количество задач для использования на практических занятиях и для самостоятельного решения, включая контрольные работы и задачи, которые могут использоваться на зачетах и при проведении экзаменов.
Для преподавателей и студентов экономических специальностей.
Рецензент: профессор, д.т.н. Рузанов А.И.
СОДЕРЖАНИЕ
| №№ | Стр. | |
| 1. | Практические занятия | |
| 1.1. | Случайные события | |
| 1.2. | Операции над событиями | |
| 1.3. | Повторные независимые испытания | |
| 1.4. | Дискретная случайная величина | |
| 1.5. | Непрерывная случайная величина | |
| 1.6. | Закон больших чисел | |
| 1.7. | Система двух случайных величин | |
| 2. | Контрольные работы | |
| 2.1. | Контрольная работа №1 | |
| 2.2. | Контрольная работа №2 | |
| 2.3. | Контрольная работа №3 | |
| 2.4. | Контрольная работа №4 | |
| 3. | Комплекты задач для проведения экзаменов и зачетов | |
| 4. | Учебная литература | |
| 5. | Приложения | |
| 5.1. | Значения функции Пуассона | |
| 5.2. | Значения функции плотности вероятности f(x) | |
| 5.3. | Значения функции Лапласа Ф(x) |
Практические занятия
|
|
1.1. Случайные события:
Основные понятия теории вероятностей: событие, вероятность события. Совместные и несовместные события. Полная группа событий. Равновозможные события. Определения вероятности: вероятность элементарного события, классическое и статистическое определение вероятности. Геометрическое определение вероятности. Элементы комбинаторики: размещения, перестановки, сочетания. Факториал. Формулы для вычисления числа размещений, перестановок, сочетаний и их использование для решения задач. Выбор с возвращением и без возвращения. Формулы для вычисления числа размещений с повторениями и сочетаний с повторениями.
1. Брошены две игральные кости. Сколько всего исходов имеет данный опыт? Найти вероятности следующих событий: 1) на каждой кости появилось четное число очков; 2) хотя бы на одной кости появилось три очка; 3) сумма очков на костях – нечетное число; 4) сумма очков на костях равна 9; 5) сумма очков делится на 3; 6) сумма выпавших очков больше их произведения; 7) на обеих костях появится одинаковое число очков; 8) сумма выпавших очков не больше 6; 9) произведение выпавших очков равно 12; 10) произведение выпавших очков не меньше 12. Какие из событий 1)-4) являются несовместными? Какие из событий 7)-10) являются несовместными? Какие из событий 1)-10) являются равновозможными?
|
|
2. Куплено два лотерейных билета. Найти вероятности следующих событий: 1) выиграют два билета; 2) выиграет хотя бы один билет; 3) выиграет только один лотерейный билет; 4) не выиграет ни один билет. Какие из этих событий являются несовместными? Какие из этих событий являются элементарными исходами данного опыта? Какие из этих событий являются равновозможными?
3. Бросаем одну монету три раза. Сколько всего элементарных исходов имеет данный опыт? Отличаются ли эти исходы от исходов опыта, в котором одновременно подбрасываются три монеты? 1) Записать все возможные исходы (события), если учитывается число выпадений герба. Составляют ли данные события полную группу? Совместны ли они? Какие из этих событий являются равновозможными? 2) Записать все возможные исходы (события), если учитывается какой стороной монета большее число раз выпала вверх. Составляют ли данные события полную группу? Совместны ли они? Какие из этих событий являются равновозможными?
4. Какова вероятность правильно набрать номер телефона, если: 1) забыта последняя цифра; 2) забыта первая цифра; 3) забыты две цифры, одна из которых – четная; 4) забыты две различные цифры и первая из них не 0?
5. Из букв разрезной азбуки составлено слово. Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал их в произвольном порядке. Найти вероятность того, что у него получится исходное слово: 1) книга; 2) мама; 3) атака; 4) машина?
6. На отдельных одинаковых карточках написаны цифры: 1, 2, 3, 4, 5, 6, 7, 8, 9. Карточки перемешивают, после чего наугад берут четыре карточки и раскладывают в ряд в порядке появления. Какова вероятность получить при этом: 1) четырехзначное четное число; 2) число 1234; 3) четырехзначное число, в котором последующая цифра больше предыдущей. Как изменятся вероятности 1)-3), если добавить карточку с цифрой 0?
|
|
7. Игровой автомат выдает комбинации из трех цифр, причем появление любой из этих комбинаций считается равновозможной. Какова вероятность выигрыша, если для этого требуется: 1) выпадение трех одинаковых цифр, за исключением 000; 2) чтобы хотя бы две любые из выпавших цифр были одинаковыми.
8. Какова вероятность того, что в январе наудачу выбранного года окажется пять воскресений?
9. Какова вероятность того, что наудачу вырванный листок из нового календаря соответствует первому числу месяца?
10. В «черном» ящике лежат 15 одинаковых на ощупь шаров, 10 из них – белые, остальные – красные. Найти вероятность того, что последовательно вынутые три шара окажутся 1) белыми; 2) красными?
11. В магазине имеется 20 пар обуви одной модели, из них 7 пар 41 размера. Найти вероятность того, что четырем покупателям подряд понадобится именно 41 размер данной модели?
12. Бросаются три игральных кости. Найти вероятность того, что на всех костях выпадет: 1) одинаковое количество очков; 2) разное число очков?
13. В старинной игре в кости необходимо было для выигрыша получить при бросании трех костей сумму очков, большую 10. Какова вероятность выигрыша?
14. Мишень представляет собой три концентрические окружности с радиусами 1, 2 и 3 соответственно. Попадание в центральный круг дает 10 очков, в кольцо, ограниченное окружностями радиусов 1 и 2 – 5 очков, во внешнее кольцо – 2 очка. В мишень случайным образом бросается точка. Определить вероятность набрать при одном броске 2, 5 или 10 очков. Каковы должны быть радиусы концентрических окружностей мишени, чтобы 2, 5 или 10 очков можно было набрать с равными вероятностями?
15. Задача о встрече. Двое договорились встретиться следующим образом: каждый приходит в условленное место в любой момент заранее оговоренного часа и ждет не более 20 минут. Какова вероятность того, что эти двое встретятся?
16. У квадратного трехчлена x2+px+q коэффициенты p и q выбраны наудачу из отрезка [-1;1]. Какова вероятность, что квадратный член имеет действительные корни?
17. Противотанковые мины поставлены на прямой через 15 метров. Танк шириной 3 метра идет перпендикулярно этой прямой. Какова вероятность, что он подорвется?
18. Парадокс Бертрана. Для некоторой окружности случайно выбирается хорда. Найти вероятность того, что эта хорда длиннее стороны правильного треугольника, вписанного в эту окружность, если: 1) середина хорды равномерно распределена в круге; 2) направление хорды задано, а ее середина равномерно распределена на диаметре, перпендикулярном направлению; 3) один конец хорды закреплен, а другой равномерно распределен на окружности.
1.2. Операции над событиями:
Противоположные события. Зависимые и независимые события. Условная вероятность. Теоремы сложения и умножения вероятностей.
Формула полной вероятности. Формула Байеса.
1. Для перечисленных ниже событий сформулировать противоположные события и найти их вероятности: 1) А – выпадение двух гербов при бросании двух монет; 2) В – вынуть белый шар из урны, в которой находятся 2 белых, 3 черных и 4 красных шара; 3) С – три попадания при трех выстрелах, вероятность попадания в цель при одном выстреле 0,8; 4) D – хотя бы одно попадание при пяти выстрелах, попадание и промах при каждом выстреле равновероятны.
2. Из колоды в 52 карты наудачу вынимается одна. Какие из перечисленных ниже событий будут независимы, а какие несовместны (рассмотреть все возможные пары событий): 1) А – появление туза; 2) В – появление красной масти; 3) С – появление бубнового туза; 4) D – появление десятки.
3. Бросаются две монеты. Найти вероятность суммы следующих событий: А – на первой монете выпал герб, В – на второй монете выпал герб двумя способами: 1) по теореме сложения; 2) используя вероятность противоположного события.
4. Из колоды в 52 карты вынимается четыре карты. Найти вероятность суммы следующих событий: А – среди вынутых карт хотя бы одна бубновая, В – среди вынутых карт хотя бы одна червонная.
5. Брошены две игральные кости. Предполагается, что все комбинации выпавших очков равновероятны. Найти условную вероятность того, что выпали две пятерки, если известно, что сумма выпавших очков делится на 5.
6. Из урны, в которой лежат 20 одинаковых на ощупь шаров: 12 белых и 8 черных, один за другим вынимаются два шара. С помощью теоремы умножения найти вероятность того, что 1) оба шара белые; 2) оба шара черные. Сравнить вероятности вынуть два разноцветных шара при условии, что 1) первый шар не возвращается в урну; 2) первый шар возвращается в урну.
7. Из урны, в которой лежат 4 красных и 6 черных шаров, один за другим вынимаются два шара. Найти вероятность того, что 1) оба шара одного цвета; 2) вынуты шары разных цветов; 3) второй вынутый шар – черный.
8. В коробке 12 карандашей трех цветов, по 4 карандаша каждого цвета. Наудачу вынимают три карандаша. Найти вероятность того, что все карандаши окажутся разного цвета при условии: 1) карандаши не возвращают в коробку; 2) вынутый карандаш возвращают в коробку.
9. Два стрелка сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка 0,8, а для второго 0,6. Найти вероятности следующих событий: 1) оба попали; 2) в мишень попал один стрелок; 3) в мишень попал хотя бы один стрелок.
10. Вероятность поражения мишени для первого стрелка 0,6. Найти вероятность поражения мишени для второго стрелка, если вероятность того, что мишень поражена два раза 0,3.
11. Вероятность одного попадания в цель при одновременном залпе из двух орудий равна 0,44.Найти вероятность поражения цели при одном выстреле первым орудием, если для второго орудия эта вероятность равна 0,8.
12. Вероятность попадания в цель при стрельбе для каждого орудия равна 0,6. Производится одновременно по одному выстрелу из трех орудий. Цель считается пораженной, если в нее попало не менее двух снарядов. Найти вероятность того, что 1) цель поражена; 2) два орудия промахнулись.
13. Три студента сдают экзамен. Вероятность получить «отлично» для первого студента равна 0,7, для второго – 0,6, для третьего – 0,2. Какова вероятность того, что экзамен будет сдан на «отлично»: 1) только одним из студентов; 2) двумя студентами; 3) хотя бы одним студентом; 4) ни одним из студентов.
14. Вероятность хотя бы одного попадания в мишень стрелком при трех выстрелах равна 0,784. Найти вероятность одного промаха при трех выстрелах.
15. Сколько раз необходимо бросить игральную кость, чтобы с вероятностью 0,9 хотя бы один раз выпало не менее 4 очков.
Формула полной вероятности (задачи 16 – 18).
16. В первой урне находится 10 шаров: 8 белых и 2 черных. Во второй 6 шаров: 5 белых и 1 черный. Из второй урны переложили в первую один шар. Какова вероятность того, что шар, извлеченный после этого из второй урны, окажется черным? Какова вероятность того, что шар, извлеченный после этого из второй урны, окажется белым?
17. Имеются две урны. В первой – 6 белых и 4 черных шара, во второй – 3 белых и 5 черных шара. Из первой урны переложили во вторую один шар, затем, перемешав шары, из второй урны в первую переложили один шар. Найти вероятность того, что шар, извлеченный после этого из первой урны, окажется белым.
18. Стрелковое отделение получило 10 винтовок, из которых 8 пристрелянных, а 2 нет. Вероятность попадания в цель из пристрелянной винтовки – 0,6, а из не пристрелянной – 0,4. Какова вероятность, что стрелок из наудачу взятой винтовки попадет в цель при одном выстреле?
Формула Байеса (задачи 19 – 21).
19. Из 25 студентов группы 5 студентов знают все 30 вопросов программы, 10 студентов выучили по 25 вопросов, 7 студентов по 20 вопросов, 3 студентов по 10 вопросов. Случайно вызванный студент ответил на два заданных вопроса. Какова вероятность, что это один из трех студентов, которые подготовили 10 вопросов.
20. Запасная деталь может находиться в одной из трех партий с вероятностями: 0,2; 0,5; 0,3. Вероятности того, что деталь проработает положенное время без ремонта, равны соответственно 0,9; 0,8; 0,7. Определить вероятность того, что деталь, проработавшая положенное время, взята из второй или третьей партии.
21. 24 человека обучаются заочно на экономическом факультете, из них 6 по специальности маркетинг, 12 по специальности менеджмент и 6 по специальности прикладная информатика. Вероятность успешно сдать все экзамены на предстоящей сессии для специальности маркетинг – 0,8; для менеджмента – 0,76; для прикладной информатики – 0,6. Найти вероятность того, что наудачу взятый студент, сдавший успешно все экзамены, окажется студентом - маркетологом.
1.3. Повторные независимые испытания:
Схема Бернулли и формула Бернулли. Формула Пуассона. Предельные случаи для формулы Бернулли: локальная и интегральная предельные теоремы.
- Найти вероятность того, что при четырех подбрасываниях игральной кости 5 очков появятся: 1) два раза; 2) хотя бы один раз.
- Вероятность выбора отличника на факультете равна 1/7. Из 28 студентов группы наудачу выбираются три студента. Определить вероятности всех возможных значений числа отличников, которые могут оказаться среди трех выбранных студентов.
- В семье 5 детей. Считая вероятности рождений мальчика и девочки одинаковыми, найти вероятность того, что в семье: 1) два мальчика; 2) не более двух мальчиков; 3) более двух мальчиков; 4) не менее двух и не более трех мальчиков.
- Сколько раз нужно подбросить игральную кость, чтобы наивероятнейшее число выпадения 6 очков было равно 50.
- Два равносильных противника играют в шахматы. Что вероятнее выиграть для каждого из них: 1) одну партию из двух или две из четырех; 2) не менее двух партий из четырех или не менее трех партий из пяти. Ничьи во внимание не принимаются.
- Бланк программированного опроса состоит из пяти вопросов. На каждый даны три ответа, один из которых правильный. Какова вероятность, что методом угадывания студенту удастся выбрать, по крайней мере, 4 правильных ответа?
7.При выпуске некоторой продукции бывает в среднем 0,5% брака. Определить вероятность того, что в партии из 800 изделий будет не более 3-х бракованных изделий.
- Вероятность того, что купюра фальшивая, равна 0,01. Найти вероятность того, что из 100 купюр: а) хотя бы одна фальшивая; б) не менее трех фальшивых.
- Вероятность неточной сборки прибора равна 0,001. Найти вероятность того, что среди 2000 собранных приборов окажется не более трех собранных неточно.
10. Вероятность того, что автомат при опускании одной монеты сработает правильно равна 0,99. Найти наиболее вероятное число случаев неправильной работы автомата и вероятность этого числа, если в автомат опущено 200 монет.
11. Установлено, что виноградник поражен вредителями в среднем на 10%. Определить вероятность того, что из 10 проверенных кустов винограда один будет поражен. Вычисления провести по формулам Бернулли, Лапласа, Пуассона. Сравнить результаты, сделать выводы.
12. На факультете 900 студентов. Вероятность дня рождения каждого студента в данный день равна 1/365. Найти вероятность того, что найдутся три студента с одним и тем же днем рождения.
13. Вероятность получения отличной оценки на экзамене равна 0,2. Найти наивероятнейшее число отличных оценок и вероятность этого числа, если экзамен сдают 75 студентов.
14. В партии семян в среднем 10% невсхожих семян. Найти вероятность того, что в партии из 2500 семян окажется от 2200 до 2350 (включительно) всхожих.
15. Вероятность погашения кредита в срок равна 0,75. Найти вероятность того, что из 200 кредитов выданных банком будет погашено в срок: а) 175 кредитов, б) не менее 140 кредитов.
16. Спортсмен попадает в цель с вероятностью 0,9. Найти вероятность того, что: а) на тренировке из ста выстрелов промахов будет не более десяти, б) на соревнованиях у этого спортсмена из десяти выстрелов будет не менее девяти попаданий.
17. Известно, что в среднем 80% кредитов, выданных банком, погашаются в срок. Найти границы, в которых с вероятностью 0,9545 будет находиться доля кредитов погашенных в срок из ста выданных.
18. В среднем 60% посетителей магазина делают в нем покупки. Найти вероятность того, в наудачу выбранный день из 200 посетителей доля, не сделавших покупок будет менее 20%.
19. Спортсмен попадает в цель с вероятностью 0,7. Найти вероятность того, что на тренировке из ста выстрелов промахов будет менее сорока.
20. В среднем продается 70% билетов на 300 мест зрительного зала театра. Найти границы, в которых с вероятностью 0,9973 будет находиться число проданных билетов в наудачу выбранный день.
21. Сколько раз следует подбросить монету, чтобы частота выпадения герба отличалась от вероятности не более чем на 0,01 с вероятностью 0,9545.
22. Какое количество повторных независимых испытаний следует провести, чтобы вероятность события отличалась от его частоты не более чем на 0,05 с вероятностью 0,9973.
23. Вероятность появления события в каждом из 400 независимых испытаний равна 0,8. Найти такое положительное число e, чтобы с вероятностью 0,9876 абсолютная величина отклонения относительной частоты от постоянной вероятности не превысила e.
24. Вероятность того, что человек в период страхования будет травмирован, равна 0,006. Компанией застраховано 1000 человек. Годовой взнос с одного человека составляет 150 рублей. В случае получения травмы застраховавшийся получает 12000 рублей. Какова вероятность того, что выплата по страховкам превысит сумму страховых взносов?
1.4. Дискретная случайная величина:
Законы распределения дискретных случайных величин. Числовые характеристики ДСВ. Математическое ожидание, дисперсия, среднее квадратическое отклонение и их свойства.
1. Вероятность работы каждого из четырех комбайнов без поломок в течение определенного времени равна 0,9. Составить закон распределения случайной величины X - числа комбайнов, работавших безотказно. Построить график распределения вероятностей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.
2. Вероятность рождения мальчика равна 0,515. Составить закон распределения случайной величины X - числа мальчиков в семьях, имеющих четырех детей. Построить график распределения вероятностей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
3. Вероятность того, что покупатель совершит покупку в магазине 0,4. Составить закон распределения случайной величины X - числа покупателей, совершивших покупку, если магазин посетило 3 покупателя. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X. Построить график распределения вероятностей.
4. В группе из 10 спортсменов 6 мастеров спорта. Отбирают (по схеме без возвращения) 3 спортсмена. Составить закон распределения случайной величины X - числа мастеров спорта из отобранных спортсменов. Найти математическое ожидание случайной величины X.
5. Стрелок производит выстрелы по цели до первого попадания. Составить закон распределения случайной величины X - числа выстрелов, сделанных стрелком. Вероятность попадания в цель при каждом выстреле составляет 0,7. Найти наивероятнейшее число выданных стрелку патронов.
6. Покупатель посещает магазины до момента приобретения нужного товара. Вероятность того, что товар имеется в определенном магазине, составляет 0,4. Составить закон распределения случайной величины X - числа магазинов, которые посетит покупатель из четырех возможных. Построить график распределения. Найти наиболее вероятное число магазинов, которые посетит покупатель.
7. Игрок поочередно покупает билеты двух разных лотерей до первого выигрыша. Вероятность выигрыша по одному билету первой лотереи составляет 0,2, а второй - 0,3. Игрок вначале покупает билет первой лотереи. Составить закон распределения и найти математическое ожидание случайной величины X - числа купленных билетов,  если игрок имеет возможность купить; а) только 5 билетов; б)* неограниченное число билетов.
если игрок имеет возможность купить; а) только 5 билетов; б)* неограниченное число билетов.
8. На конноспортивных соревнованиях необходимо преодолеть четыре препятствии с вероятностями, равными соответственно 0,9; 0,8; 0,7; 0,6. При первой неудаче спортсмен в дальнейших состязаниях не участвует. Составить закон распределения случайной величины X - числа взятых препятствий. Найти математическое ожидание случайной величины X.
9. В игре спортивной лотереи угадывается 5 номеров из 36. Игрок получает выигрыш, если угадает 5,4 или 3 номера. За 5 угаданных номеров выигрыш составляет 10 тыс. руб. Сумма выигрыша по одной карточке за 4 правильно угаданных номера в 10 раз больше, чем за 3. Составить закон распределения случайной величины Х-числа правильно угаданных номеров. Определить среднюю величину выигрыша, если известно; что карточек было выпущено 1 млн. шт. Стоимость одной карточки 1 руб. Выигрыши составляют 50 % общей суммы тиража.
10. Предприниматель рассматривает возможность покупки акций трех предприятий, по каждой из которых известна доходность, как отношение величины получаемого дохода за период времени к цене акции, и вероятности возможных значений доходности. Акции какого предприятия следует считать более доходными, если руководствоваться средним значением (математическим ожиданием) доходности?
| Предприятие 1 | Предприятие 2 | Предприятие 3 | |||
| Доходность (%),X | Вероятность, Рx | Доходность(%),Y | Вероятность, Рy | Доходность (%),Z | Вероятность, Pz |
| 0,2 | 0,1 | 0,1 | |||
| 0,3 | 0,4 | 0,4 | |||
| 0,4 | 0,3 | 0,25 | |||
| 0,1 | 0,2 | 0,25 |
Акции какого предприятия являются менее рискованными (считая, что чем выше колеблемость доходности акций, тем больше их рискованность)?
11. Бросают 12 игральных костей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X - суммы числа очков, которые могут появиться на всех выпавших гранях.
12. Математическое ожидание случайной величины X равно 8. Найти математическое ожидание случайных величин: а) Х-4; б) Х+6; в) ЗХ-4; г) 4Х+3.
13. Дисперсия случайной величины X равна 8. Найти дисперсию следующих величин: а) Х-2; б) Х+6; в) ЗХ-2; г) 2Х+7.
14. Найти математическое ожидание и дисперсию случайных величин: a) Z=4X-2Y; б) Z=2X-4Y; в) Z=3X+5Y; если М(Х)=5, M(Y)=3, D(X)=4, D(Y)=6. Случайные величины X и Y независимы.
15. Случайные величины X и Y независимы. Найти математическое ожидание и дисперсию случайных величин:a) Z=4X+2Y; б) Z= 5X-3Y; в) Z=3X-Y, если М(X)=6, M(Y)=5, D(X)=5, D(Y)=4. Случайные величины X и Y независимы.
16. Вероятность изготовления бракованной детали автоматом равна 0,002. Найти математическое ожидание и среднее квадратическое отклонение случайной величины X - числа бракованных деталей, если деталей изготовлено 1000. Определить вероятность того, что из 1000 деталей будет изготовлено: а) не более двух бракованных; б) хотя бы одна бракованная.
17. Независимые случайные величины X и Y имеют следующие распределения:
| Xi | Yi | ||||||
| Pi | 0,3 | 0,5 | 0,2 | Pi | 0,4 | 0,6 |
Составить закон распределения случайных величин: a) Z=X+Y; б) V=XY. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайных величин Z и V.
18. Дискретная случайная величина X принимает три возможных значения: х1=1 с вероятностью р1=0,2; x3=5 с вероятностью 0,3 и x2с вероятностью р2. Найти x2и р2, если известно, что М (Х)=3.
19. Вероятность сдать экзамен студентом на «отлично» равна 0,3, на «хорошо» - 0,4. Определить вероятности получения других оценок (2; 3), если известно, что М(Х)=3,9.
20. Вероятность выигрыша по лотерейному билету составляет 0,02. Найти М(Х) и s(Х) числа выигранных билетов, если их было приобретено 100.
21. По одному тиражу лотереи куплено 100 билетов. Среднее квадратическое отклонение числа выигранных билетов равно трем. Найти вероятность выигрыша по одному билету лотереи.
22. Подброшены две игральные кости. Найти М(Х), где X - случайная величина - сумма числа очков, которые могут появиться на двух выпавших гранях.
1.5. Непрерывная случайная величина:
Интегральная функция распределения и ее свойства. Дифференциальная функция распределения и ее свойства. Законы распределения непрерывных случайных величин. Числовые характеристики НСВ.
1. По данным задач1, 3, 4, 8 занятия 1.4 составить интегральную функцию случайной величины X и начертить ее график..
2. Найти интегральную функцию распределения случайной величины X - числа попаданий в цель, если произведено три выстрела с вероятностью попадания в цель при каждом выстреле 0,8.
3. Вероятность сдачи первого экзамена студентом составляет 0,7, второго 0,6 и третьего 0,8. Найти интегральную функцию случайной величины X - числа экзаменов, сданных студентом. Определить М(Х).
4. Случайная величина X задана интегральной функцией F(x):
 |
Найти вероятность того, что в результате испытания случайная величина X примет значение: а) меньше 0; б) меньше 1; в) не меньше 1; г) заключенное в интервале (0;2).
5. Дана интегральная функция случайной величины X F(x):
 |
Найти вероятность того, что в результате шести испытаний случайная величина X два раза примет значение, принадлежащее интервалу (0;1).
6. Случайная величина X задана интегральной функцией F(x):
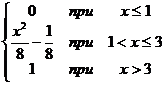 |
Найти: а) дифференциальную функцию случайной величины X; б) математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины X; в) вероятность попадания случайной величины в интервал (1;2).
7. Дана функция распределения случайной величины X F(x):
 |
а) Определить вероятность попадания случайной величины в интервал (-а;а). б) Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.
8. Случайная величина X задана интегральной функцией F(x):
 Найти значения А и В, математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.
Найти значения А и В, математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.
9. Случайная величина X задана интегральной функцией F(x). Найти: а) дифференциальную функцию случайной величины X; б) вероятность того, что в результате четырех независимых испытаний случайная величина X хотя бы один раз примет значение, принадлежащее интервалу (1;1,5); в) начертить графики функций.
 |
F(x) =
10. Случайная величина X задана дифференциальной функцией f(x). Найти: а) интегральную функцию; б) вероятность попадания случайной величины в интервал (a/6;a/3).
 |
f(x) =
11. Случайная величина X задана дифференциальной функцией f(x). Найти: а) интегральную функцию случайной величины X и начертить её график; б) вероятность попадания случайной величины X в интервал (-1;1/3); в) математическое ожидание, дисперсию и среднее квадратическое отклонение.
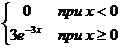 |
f(x) =
12. Случайная величина X задана дифференциальной функцией f(x). Найти: а) постоянную С; б) математическое ожидание, дисперсию и среднее квадратическое отклонение.
f(x) = 
13. Случайная величина X задана дифференциальной функцией f(x). Найти: постоянную С.
 |
f(x) =
14. НСВ X имеет плотность вероятности (закон Коши): f(x) = С/(1+х2). Найти: а) постоянную С; б) функцию распределения F(x); в) вероятности попадания в интервалы (-1; 1); (-  ;
;  ); г) построить графики f(x), F(X).
); г) построить графики f(x), F(X).
Равномерный закон распределения (задачи 15 – 17).
15. Случайная величина X равномерно распределена в интервале (-2;N). Найти: а) дифференциальную функцию случайной величины X; б) интегральную функцию; в) вероятность попадания случайной величины в интервал (-1;N/2); г) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.
16. Найти математическое ожидание и дисперсию случайной величины, равномерно распределенной в интервале: а) (5, 11); б) (-3; 5). Начертить графики этих функций.
17. Равномерно распределенная случайная величина X задана плотностью распределения f(x) = 0,125 в интервале (а-4; а+4), вне его f(x) = 0. Найти М(Х), Д(Х), s(Х).
Показательный закон распределения (задачи 18 – 24).
18. Написать дифференциальную и интегральную функции распределения показательного закона, если: а) параметр l=2; б) l=5; в) l=0,5.
19. Случайная величина X распределена по показательному закону, причем l=2. Найти вероятность попадания случайной величины X в интервал: а) (0; 1); б) (2; 4).
20. Найти М(Х), D(X), s(Х) показательного закона распределения случайной величины X заданной функцией F(x):
 |
F(x) =
Если: а) l=0,4; б) l=3; в) l=4.
21. Испытываются два независимо работающих элемента. Длительность безотказной работы первого имеет показательное распределение F1(t) = 1 -  , второго F2(t) = 1 -
, второго F2(t) = 1 -  •. Найти вероятность того, что за время длительностью 20 часов: а) оба элемента будут работать; б) откажет только один элемент; в) откажет хотя бы один элемент; г) оба элемента откажут.
•. Найти вероятность того, что за время длительностью 20 часов: а) оба элемента будут работать; б) откажет только один элемент; в) откажет хотя бы один элемент; г) оба элемента откажут.
22. Вероятность того, что оба независимых элемента будут работать в течение 10 суток равна 0,64. Определить функцию надежности для каждого элемента, если функции одинаковы.
23. Среднее число ошибок, которые делает оператор в течение часа работы равно 2. Найти вероятность того, что за 3 часа работы оператор сделает: а) 4 ошибки; б) не менее двух ошибок; в) хотя бы одну ошибку.
24. Среднее число вызовов, поступающих на АТС в одну минуту, равно трем. Найти вероятность того, что за 2 минуты поступит: а) 4 вызова; б) не менее трех вызовов.
Нормальный закон распределения (задачи 25 – 33).
25. Для исследования продуктивности определенной породы домашней птицы измеряют диаметр яиц. Наибольший поперечный диаметр яиц представляет собой случайную величину, распределенную по нормальному закону со средним значением 5 см и средним квадратическим отклонением 0,3 см. Найти вероятность того, что: а) диаметр взятого наудачу яйца будет заключен в границах от 4,7 до 6,2 см; б) отклонение диаметра от среднего не превзойдет по абсолютной величине 0,6 см.
26. Вес вылавливаемых в пруду рыб подчиняется нормальному закону распределения со средним квадратическим отклонением 150 г и математическим ожиданием а = 1000 г. Найти вероятность того, что вес пойманной рыбы будет: а) от 900 до 1300 г; б) не более 1500 г; в) не менее 800 г; г) отличаться от среднего веса по модулю не более чем на 200 г; д) начертить график дифференциальной функции случайной величины X.
27. Урожайность озимой пшеницы по совокупности участков распределяется по нормальному закону с параметрами: а = 50 ц/га, s = 10 ц/га. Определить: а) какой процент участков будет иметь урожайность свыше 40 ц/га; б) процент участков с урожайностью от 45 до 60 ц/га.
28. Выборочным методом измеряется засоренность зерна, случайные ошибки измерения подчинены нормальному закону распределения со средним квадратическим отклонением 0,2 г и математическим ожиданием а = 0. Найти вероятность того, что из четырех независимых измерений ошибка хотя бы одного из них не превзойдет по абсолютной величине 0,3 г.
29. Количество зерна, собранного с каждой делянки опытного поля, есть нормально распределенная случайная величина X, имеющая математическое ожидание m = 60 кг и среднее квадратическое отклонение равно 1,5 кг. Найти симметричный относительно m интервал, в котором с вероятностью 0,9906 будет заключена величина X. Написать дифференциальную функцию этой случайной величины.
30. С вероятностью 0,9973 было установлено, что абсолютное отклонение живого веса случайно взятой головы крупного рогатого скота от среднего веса животного по всему стаду не превосходит 30 кг. Найти среднее квадратическое отклонение живого веса скота, считая, что распределение скота по живому весу подчиняется нормальному закону.
31. Урожайность овощей по участкам является нормально распределенной случайной величиной с математическим ожиданием 300 ц/га и средним квадратическим отклонением 30 ц/га. С вероятностью 0,9545 определить симметричные относительно математического ожидания границы, в которых будет находиться средняя урожайность овощей на участках.
32. Нормально распределенная случайная величина X задана дифференциальной функцией f(x). Определить: а) вероятность попадания случайной величины в интервал (3; 9); б) моду и медиану случайной величины X.
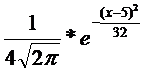 |
f(x) =
33. Случайная величина распределена по нормальному закону с математическим ожиданием а = 20. Вероятность попадания ее в интервал (20; 30) равна 0,4772. Определить вероятность попадания случайной величины в интервал (10; 25).
34. Случайная величина X распределена по закону прямоугольного треугольника в интервале (0; а). Найти: а) дифференциальную функцию случайной величины X; б) интегральную функцию; в) вероятность попадания сл