Примеры выполнения задания

Пример 1. Кривошип О₁О = l вращается вокруг оси, проходящей через точку О ₁, и имеет в данный момент угловую скорость w и угловое ускорение e (рис. 33, а). На палец О этого кривошипа свободно насажано колесо 1 радиуса r, которое катится при этом без скольжения по неподвижному колесу радиуса

R = l – r.

Найти в данный момент времени угловую скорость w _I и угловое ускорение e_I колеса 1, скорости и ускорения точек А и В.

Решение

Механизм состоит из двух тел: кривошип О ₁ О - совершает вращательное движение и колесо 1 совершает плоскопараллельное движение.

Для решения задачи надо рассмотреть движение колеса I. По данным задачи легко найти скорость` u <sub>0</sub> и ускорения` a ₀ точки О этого колеса, которую и примем за полюс.

Определение` u <sub>0</sub> и` a ₀. Зная w и e кривошипа, находим:

u₀ = w О₁О = w l,

.

Направления векторов 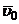и определяются направлением w и e, вектор 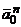направлен от O к O ₁. Показываем их на рисунке.

Определение w_I,` υ<sub>А</sub>, ` υ_B. Точка Р зацепления колес является МЦС для шестерни 1; следовательно, угловая скорость шестерни I равна:

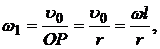(a)

а направление w _I определяется направлением` υ _о.

Зная w _I и МЦС колеса I, находим скорости точек А и В:

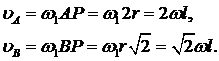
Векторы ` υ<sub>А</sub> и `υ_B направлены перпендикулярно к АР и ВР и их направления определяются направлением w_I.

Определение e_I. Так как в выражении (а) величина ОР=r остается постоянной при любом положении колеса 1, то

.

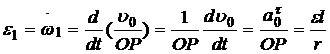и` υ₀ направлены в разные стороны, так как вращение колеса 1 замедленное, направлено противоположно w₁.

Определение ускорений точек А и В. Перейдя к колесу 1, приняв точку О за плюс, имеем:

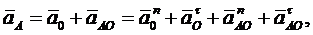(б)

(в)

Находим:

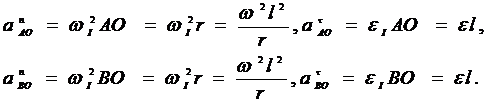
Векторы 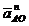и 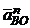направлены от рассматриваемых точек к полюсу, а векторы 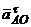и 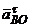перпендикулярны им, и их направления определяются направлением e _I (рис. 33).

Изображаем на рисунке все векторы, из которых слагаются ускорения точек А и В, и спроецировав (б) и (в) на оси координат, получим:

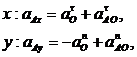
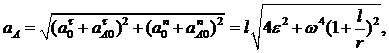
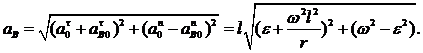
Ответ:

Пример 2.Механизм состоит из стержней 1, 2, 3, 4 и ползуна В, соединенных друг с другом и с неподвижными опорами О₁ и О₂ шарнирами (рис. 34), точка Д находится в середине стержня 2.

Длины стержней равны соответственно: l ₁=0,4 м; l ₂=1,2 м; l ₃=1,4 м;

l ₄=0,6 м. Для положения механизма, показанного на рисунке, по известной угловой скорости w ₁=2 c ^-1 угловому ускорению e ₁=4 c ^-2 стержня О₁А в данный момент времени найти скорости ` υ<sub>B</sub> и `u_Е точек B и E, угловую скорость w_AB и угловое ускорение e_AB звена AB, а также ускорение точки B.

 

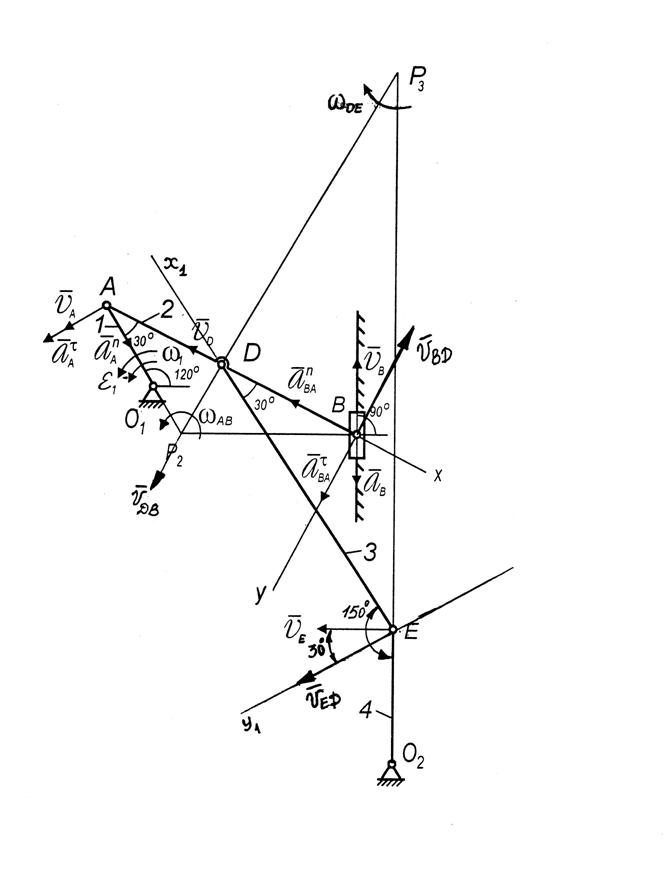Рисунок 34

Расчетная схема

 

 

Решение

 

I. Механизм образуют 4 тела: 1 – О₁А – совершающее вращательное движение; 2 – АВ – плоскопараллельное движение; 3 – ДЕ – плоско - параллельное движение; 4 – О ₂ Е – вращательное движение. Начинаем с рассмотрения движения тела 1, найдем 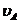. Это точка принадлежит телу О ₁ А, совершающему вращательное движение, поэтому υ_B. скорость точки А равна

,

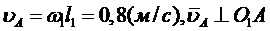направление ` υ_A определяется направлением w₁.

Для определения ` υ<sub>B</sub> воспользуемся теоремой о проекции скоростей двух точек стержня АВ на прямую, соединяющую точки А и В. Скорость ` υ_B направлена вдоль направляющих. Находим:

υ_A cos 60⁰= υ_B cos 60⁰, отсюда υ_B = υ_A = 0,8 м/с.

Определение w_AB. Для этого находим МЦС – Р₂ звена АВ, восстанавливая из точек А и В перпендикуляры к` υ<sub>A</sub> и` υ_B. Находим AP₂ = AD/cos 30⁰=0,69 м, и w_AB=υ_A / AP ₂=1,16 c^-1. Направление w_AB определяется направлением υ_A.

Определение ` υ<sub>E</sub>. Точка E принадлежит стержню ДЕ. Следовательно, для определения ` υ_E надо предварительно найти ` υ_Д. Так как точка Д принадлежит одновременно стержню АВ, то υ_Д = w_AB ДР ₂ = (υ_A/AP ₂) ДР ₂ = 0,40 м/с.

Вектор υ_Д перпендикулярен отрезку Р₂Д и направлен в соответствии с направлением w_АВ.

Так как точка Е принадлежит одновременно стержню О₂Е, вращающемуся вокруг точки О₂, то ` υ<sub>E</sub>┴ O<sub>2</sub>E. Е одновременно принадлежит и ДЕ, поэтому восстанавливая из точек Д и Е перпендикуляры к ` υ_E и ` υ_Д, получаем МЦС Р₃ звена ДЕ. Так как ÐДЕР₃=ÐДР₃Е =30⁰, то D ДР ₃ Е равнобедренный. Составив пропорцию, находим, что

.

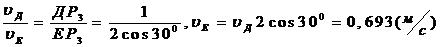По направлению` υ<sub>Д</sub> определяем направление поворота стержня ДЕ (w<sub>ДЕ</sub>), вектор` υ_Е будет направлен в сторону поворота этого стержня перпендикулярно к Р₃Е.

Определение 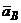. Находим сначала ускорение точки А

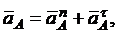
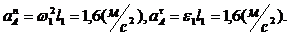
Вектор 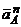направлен вдоль AO ₁, а 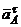– перпендикулярно АО ₁; изображаем эти векторы на рисунке.

Приняв А за полюс и применяя теорему об ускорении к В, получим

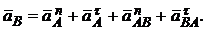
Находим 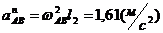. Вектор направлен от В и А. Вектор 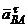направлен перпендикулярно АВ (конкретное направление выберем предположительно). Изображаем на рисунке эти векторы.

Для нахождения 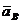последнее векторное равенство спроецируем на ось х, перпендикулярную .

Так как точка В одновременно принадлежит и ползуну, имеющему направляющие, то предполагаем, что 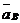направлен вниз.

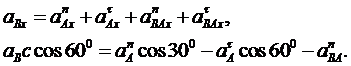
Отсюда, подставляя числовые значения всех величин, находим = -2,05 м/с². Знак минус указывает, что вектор 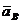направлен в сторону, противоположную указанному на рисунке.

Определение e_АВ. Для определения e_АВ сначала определим 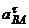. Для этого последнее векторное равенство спроецируем на ось Вy:

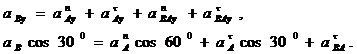
Отсюда находим 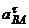= -3,96 м/с². Знак указывает, что 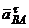направлен противоположно показанному на рисунке.

Из равенства = e_АВ l ₃ определяем

.

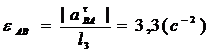Так как 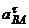< 0, то e_AB направлено против направления движения часовой стрелки (противоположно первоначально предполагаемому направлению).

Ответ: υ_В =0,8 м/с, υ_Е =6,93 м/с, w_АВ =1,16 с^-1, e_АВ =3,3 с^-2, =2,05 м/с².

Пример 3.К кривошипу, равномерно вращающемуся вокруг оси О с угловой скоростью w_ОА = 4 с^-1, прикреплен шатун АВ с коромыслом ВС (рис. 33). Даны размеры: ОА = r =0,5 м, АВ =2 r, ВС = r Ö2. В положении, изображенном на рисунке, Ð ОАВ =90⁰, Ð АВС =45⁰. Определить для этого положения ускорение точки В, а также угловую скорость и угловое ускорение коромысла ВС и шатуна АВ.

 

Рисунок 35

Расчетная схема

Решение

 

Рассмотрим движение тел, образующих механизм: 1 – ОА – вращательное; 2 – АВ – плоско – параллельное; 3 – ВС – вращательное.

Решение начнем с ОА, найдем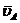

.

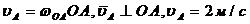Определение 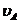и 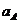. Рассматривая движение шатуна АВ, выберем за полюс точку А, принадлежащую одновременно и кривошипу ОА, совершаемому вращательное движение. Для точки А, так как w_ОА - const, получаем:

= w_OA OA = w_OA r = 2 (м/с),

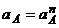= w²_OA OA = w²_OA r = 8 (м/с²).

Вектор` υ_А перпендикулярен ОА, его направление определяется w_ОА, а вектор 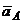направлен от А к О.

Определение w_АВ. В связи с тем, что точка В принадлежит одновременно звену ВС, вектор`υ<sub>В</sub> перпендикулярен звену ВС. Проводя перпендикуляры к` υ _a и` υ_В, получаем МЦС звена АВ - Р_АВ. Из DАР_АВВ следует, что АР_АВ = АВ =2 r, а поэтому

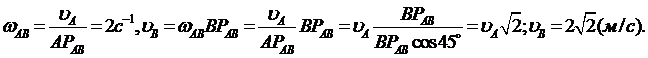
Направление поворота показано на рисунке.

Ускорение точки В. По теореме об ускорениях точки при плоском движении твердого тела имеем

.

В этом выражении направление и величина неизвестны. Кроме того, неизвестна величина 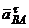, так как для определения e_АВ нельзя воспользоваться приемом, примененным в примере 1 (расстояние до МЦС от точки А не постоянное).

С другой стороны, точка В принадлежит звену ВС, а потому

.

Здесь легко найти , но нельзя найти величину 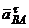, так как неизвестно e_BC. Приравнивая правые части двух последних векторных равенств, имеем

.

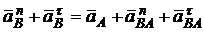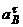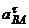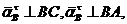Здесь будут неизвестными только численные значения величин и , направления выбираем предположительно. В проекциях на оси это векторное равенство дает два скалярных уравнения, из которых эти неизвестные и определяются.

Предварительно найдем и .

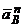Определение . Зная w_АВ, находим

= w ²_АВ AB = 4 (м/с²).

Вектор направлен от В к А.

Определение .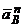

Зная υ_В находим

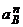= υ ²_B/ BC = 8Ö2 (м/с²).

Вектор 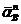направлен от В к С.

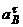Определение и . Для определения спроецируем обе части векторного равенства на оси координат х и у

х: 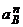cos 45⁰ + 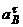cos 45⁰ = ,

у: .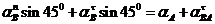

Подставляя численные значения величин, получаем 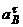= - 4Ö2 (м/с²), .

Знак минус показывает, что вектор 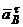имеет направление, противоположное выбранному, следовательно ` υ_B (вращение ВС замедленное).

Зная 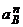и 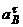, находим :

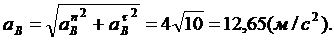
Определение w_ВС, e_ВС и ε_АВ. По известным υ_B и 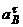и определяем

w_ВС = υ_B / BC = 4 (c^-1), e_BC=| 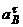|/ ВС =8 (с^-2), .

Направление w_ВС определяется направлением ` υ<sub>B</sub>, а e<sub>ВС</sub> – истинным направлением ` , истинным направлением . Указываем w_ВС и e_ВС на рисунке.

Ответ: w_ВС = 4 с^{- 1}, w_АВ =2 с^-1, e_АВ = 20 с^{- 2}, e_ВС = 8 с^-2, = 12,65 м/с².

6 Задачи и вопросы для самоконтроля

1. Скорость груза 1 v =0,5 м/с (рис. 36). Определить угловую скорость подвижного блока 2, если его радиус R =0,1 м. (Ответ: 2,5 с ^-1).

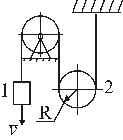
Рисунок 36

К задаче 1

Рисунок 37

к задаче 2

 

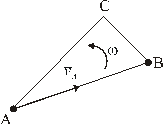
Рисунок 38

к задаче 3

2. Стержень АВ длиной 80 см движется в плоскости чертежа. В некоторый момент времени точки А и В стержня имеют скорости v_A =0,2 м/с, v_B =0,6 м/с (рис. 37). Определить угловую скорость стержня. (Ответ: 0,5 с^-1).

3. Скорость точки А плоской фигуры АВС v_А =2 м/с, угловая скорость

фигуры w =2 рад/с (рис. 38) расстояние АВ= 1,5 м. Определить скорость точки В. (Ответ: 3,61 м/с).

4. Для заданного положения шарнирного четырехзвенника (рис. 39). Определить скорость точки В, если точка А имеет скорость 1 м/с.

(Ответ: 0,577 м/с).

5. Кривошип ОА механизма, вращаясь равномерно, образует в данный момент времени с направлением ОВ угол j =90° (рис. 40). Определить расстояние от мгновенного центра скоростей шатуна АВ до ползуна В. (Ответ: ¥).

6. Определить скорость точки В колеса (рис. 41), если точка А колеса имеет скорость 2 м/с. (Ответ: 1,41 м/с).

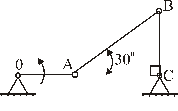
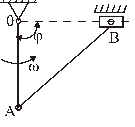
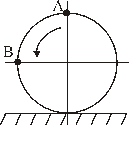
Рисунок 39 Рисунок 40 Рисунок 41