Кафедра оборудования и автоматизации машиностроения
|
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовой работе по дисциплине
МЕХАНИКА АВТОМАТИЧЕСКИХ УСТРОЙСТВ
 |
Вариант 10

Выполнил студент группы АМ-10-1 Нгуен Ш. Х.
шифр группы подпись Фамилия И. О.
Курсовая работа защищена
с оценкой:_____________
Иркутск 2012
Курсовая работа: Уравнение лагранжа II рода
Задание: Применение уравнений Лагранжа II рода к определению сил и моментов, обеспечивающих программное движение манипулятора.(Вариант 10).
Манипулятор, состоящий из звеньев 1,2 и захвата D, приводится в движение приводами А и В. Захват D перемещается вдоль прямой ОN. Со стороны привода А к звену 1 прикладывается управляющее усилие  . Привод В воздействует на звено 2 моментом
. Привод В воздействует на звено 2 моментом  .
.
Перемещение звена 2 манипулятора ограничено препяствиями К и L, поэтому изменение угла поворота 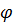 =
=  этого звена возможно лишь в интервале
этого звена возможно лишь в интервале  , где
, где  - время движения звена.
- время движения звена.
Следуюшие условия удовлетворяются:

Програмнные движения звена 1, удовлетворяющие требованиям «мягкого» касания, приняты в таком виде:

Таблица исходных данных:

| 
| 
| 
| 
|  ,м ,м
|  , , 
| 
| 
|

| 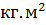
| 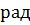
| ||||||
| 3,5 | - | 1,4 | 1,6 | 0,4 | 0,1 
|  /6 /6
|
 - масса первого звена, захвата и переносимого в захвате обьекта;
- масса первого звена, захвата и переносимого в захвате обьекта;
 - масса второго звена;
- масса второго звена;
 - момент инерции первого звена, захвата и переносимого в захвате обьекта относительно главной центральной оси инерции;
- момент инерции первого звена, захвата и переносимого в захвате обьекта относительно главной центральной оси инерции;
 - момент инерции второго звена;
- момент инерции второго звена;
Центр тяжести звена 1 находится в точке А.
Требуется:
1. Вычислить значение управляющих сил и моментов в начале торможения звена 1. Считать, что торможение звена 1 начинается в тот момент, когда угловое ускорение звена обращается в ноль.
2. Построить графики зависимости управляющих моментов и сил от времени.
Рисунок:

Будем рассматривать механическую систему как систему с двумя степенями свободы, приняв за обобщенные координаты угол 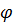 поворота звена 2 и смещение s звена 2.
поворота звена 2 и смещение s звена 2.
Для рассмаириваемой системы можно записать:
 (1)
(1)
Эти равенства играют роль уравнений связей.
В соответствии с выбраными обобщенными координатами имеем:
 (2)
(2)
Совокупность уравнений позволяет составить дифференциальные уравнения движения механической системы.
Кинематическая энергия системы равна сумме кинетической энергии  звена 1 и
звена 1 и  звена 2.
звена 2.

Где

Продиференцировав (1) по времени, будем иметь

Откуда

Таким образом

Найдем значения слагаемых уравнений Лагранжа:
 (3)
(3)
Определим обобщенные силы  .
.
Из выражений работы сил на элементарных перемещениях системы, соответствующих вариации каждой обобщенной координаты:

Мы получим
 (4)
(4)
 (5)
(5)
Подставляя (3),(4),(5) в (2), есть:
 (6)
(6)
Так как захват D должен двигаться вдоль прямой, перпендикулярной оси  , намеханизм дополнительно оказывается наложенной связь
, намеханизм дополнительно оказывается наложенной связь

Или

Следовательно,

Отсюда

Поставляя (7), (8) в (6), приходим к соотношениям
 (9)
(9)
Равенства (9) представляют собой зависимость управляющего момента М и управляющего усилиния Р от известных функций  ,
,  и
и 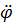 . Так как
. Так как  является заданной функцией времени, то вычисление производных
является заданной функцией времени, то вычисление производных  и
и 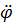 , а следовательно, и М и Р не представляет труда.
, а следовательно, и М и Р не представляет труда.
Вычислим М и Р в момент начала торможения звена 1.
В этот момент угловое ускорение 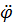 обращается в нуль. Производные
обращается в нуль. Производные  и
и 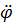 соответственно равны:
соответственно равны:


Отсюда
 и
и 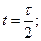
Таким образом, торможение звена 1 начинается в момент времени  . В этот момент времени:
. В этот момент времени:
 (10)
(10)
Имеем:

Подставпяя (10) в (9) получаем:
+ 
Имеем
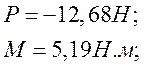
График управляющей силы Р:

График управляющего момента М: