Министерство образования Тверской области
Государственное бюджетное профессиональное образовательное учреждение
«Бологовский колледж»
Реферат
Тема «Понятие дифференциала и его приложения, выпуклость и точки перегиба.»
Работу выполнил
студент 22 группы
Голубев Владислав
г.Бологое
Дифференциалом функции называется линейная относительно 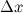 часть приращения функции. Она обозначается как
часть приращения функции. Она обозначается как  или
или  . Таким образом:
. Таким образом:

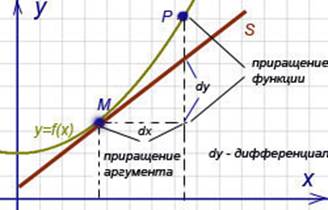
Геометрический смысл дифференциала. Дифференциал функции y = f (x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x; y), при изменении x (аргумента) на величину 
Дифференциал,  является главной, линейной относительно
является главной, линейной относительно  частью приращения функции; чем меньше
частью приращения функции; чем меньше  , тем большую долю приращения составляет эта часть. В этом можно убедиться, мысленно передвигая перпендикуляр, опущенный из точки P (см. рисунок) к оси Ox, ближе к началу координат. Поэтому при малых значениях
, тем большую долю приращения составляет эта часть. В этом можно убедиться, мысленно передвигая перпендикуляр, опущенный из точки P (см. рисунок) к оси Ox, ближе к началу координат. Поэтому при малых значениях  (и при
(и при  ) приращение функции можно приближенно заменить его главной частью
) приращение функции можно приближенно заменить его главной частью  , т.е.
, т.е.

Свойства дифференциала
Пусть u и v − функции переменной x. Дифференциал обладает следующими свойствами:
1. Постоянный коэффициент можно выносить за знак дифференциала:
d(Cu)=Cdu, где C − постоянное число.
2. Дифференциал суммы (разности) функций:
d(u±v)=du±dv.
3. Дифференциал постоянной величины равен нулю:
d(C)=0.
4. Дифференциал независимой переменной x равен ее приращению:
dx=Δx.
5. Дифференциал линейной функции равен ее приращению:
d(ax+b)=Δ(ax+b)=aΔx.
6. Дифференциал произведения двух функций:
d(uv)=du⋅v+u⋅dv.
7. Дифференциал частного двух функций:
d(uv)=du⋅v−u⋅dvv2.
8. Дифференциал функции равен произведению производной на дифференциал аргумента:
dy=df(x)=f′(x)dx.
Как видно, дифференциал функции dy отличается от производной лишь множителем dx. Например,
d(xn)=nxn−1dx,d(lnx)=dxx,d(sinx)=cosxdx
и так далее.
Выпуклость функции, точки перегиба
График дифференцируемой функции называется выпуклым в интервале если он расположен ниже любой своей касательной на этом интервале.
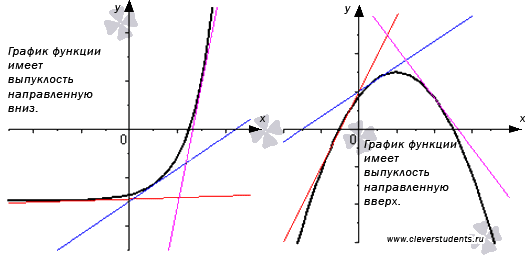
Точка  называется точкой перегиба графика функции y=f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки
называется точкой перегиба графика функции y=f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки  , в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости.
, в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости.
Другими словами, точка М называется точкой перегиба графика функции, если в этой точке существует касательная и график функции меняет направление выпуклости, проходя через нее.

Необходимое условие существования точки перегиба функции  .
.
Если функция  дважды непрерывно дифференцируема в окрестности точки
дважды непрерывно дифференцируема в окрестности точки  и точка
и точка  является точкой перегиба функции
является точкой перегиба функции  , то
, то 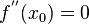 .
.
Достаточные условие существования точки перегиба.
Если функция  дважды дифференцируема в некоторой выколотой окрестности точки
дважды дифференцируема в некоторой выколотой окрестности точки 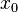 и
и  меняет знак при переходе через
меняет знак при переходе через  , то точка
, то точка  является точкой перегиба функции
является точкой перегиба функции  .
.
Если функция  в некоторой окрестности точки
в некоторой окрестности точки 
 раз непрерывно дифференцируема, причем
раз непрерывно дифференцируема, причем  нечётно и
нечётно и  , и
, и 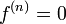 при
при  , а
, а  , то точка
, то точка  является точкой перегиба функции
является точкой перегиба функции  .
.