Определитель матрицы – это число, характеризующее квадратную матрицу А и тесно связанное с решением систем линейных уравнений. Определитель матрицы А обозначается 
или 
. Любой квадратной матрице А порядка n ставится в соответствие по определенному закону вычисленное некоторое число, называемое определителем, или детерминантом, n-го порядка этой матрицы. Рассмотрим определители второго и третьего порядков.
Пусть дана матрица
,
тогда ее определитель второго порядка вычисляется по формуле
.
Пример. Вычислить определитель матрицы А:
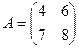
Ответ: -10.
Определитель третьего порядка вычисляется по формуле
.
Пример. Вычислить определитель матрицы В
.
Ответ: 83.
Вычисление определителя n-го порядка производится на основании свойств определителя и следующей теоремы Лапласа: определитель равен сумме произведений элементов любой строки (столбца) матрицы на их алгебраические дополнения:
.
Алгебраическое дополнение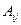 
элемента 
равно 
, где 
- минор элемента , получаемый путем вычеркивания в определителе i-ой строки и j-го столбца.
Минором порядка элемента 
матрицы А называется определитель матрицы (n-1)-го порядка, полученный из матрицы А вычеркиванием i-ой строки и j-го столбца.
Пример. Найти алгебраические дополнения всех элементов матрицы А:
.
Ответ: 
.
Пример. Вычислить определитель матрицы треугольной матрицы:
.
Ответ: -15.
Свойства определителей:
1. Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.
2. Если все элементы какой-либо строки (столбца) матрицы умножить на число 
, то ее определитель умножится на это число.
3. При транспонировании матрицы ее определитель не изменится.
4. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
5. Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.
6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
7. Сумма произведения элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0.
8. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.
9. Сумма произведений произвольных чисел 
на алгебраические дополнения элементов любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа .
10. Определитель произведения двух квадратных матриц равен произведению их определителей.
Обратная матрица.
Определение. Матрица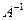 
называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:
.
Из определения следует, что только квадратная матрица имеет обратную; в этом случае и обратная матрица является квадратной того же порядка. Если определитель матрицы отличен от нуля, то такая квадратная матрица называется невырожденной.
Необходимое и достаточное условие существования обратной матрицы: Обратная матрица 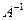существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная.
Первый алгоритм вычисления обратной матрицы:
1. Находим определитель исходной матрицы. Если определитель не равен нулю, то исходная матрица невырожденная и обратная матрица существует.
2. Находим матрицу 
, транспонированную к А.
3. Находим алгебраические дополнения элементов транспонированной матрицы и составляем из них присоединенную матрицу 
.
4. Вычисляем обратную матрицу по формуле: 
.
5. Проверяем правильность вычисления обратной матрицы, исходя из ее определения .
Пример. Найти матрицу, обратную к данной:
.
Ответ: 
.
Второй алгоритм вычисления обратной матрицы:
Обратную матрицу можно вычислить на основании следующих элементарных преобразований над строками матрицы:
- перемена местами двух строк;
- умножение строки матрицы на любое число, отличное от нуля;
- прибавление к одной строке матрицы другой строки, умноженной на любое число, отличное от нуля.
Для того чтобы вычислить обратную матрицу для матрицы А, необходимо составить матрицу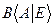 
, затем путем элементарных преобразований привести матрицу А к виду единичной матрицы Е, тогда на месте единичной матрицы получим матрицу .
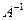Пример. Вычислить обратную матрицу для матрицы А:
.
Составляем матрицу В вида:
.
Элемент 
= 1 и первую строку, содержащую данный элемент, назовем направляющими. Осуществим элементарные преобразования, в результате которых первый столбец преобразуется в единичный столбец с единицей в первой строке. Для этого ко второй и третьей строкам прибавим первую строку, соответственно умноженную на 1 и -2. В результате этих преобразований получим:
.
Окончательно получим
.
Откуда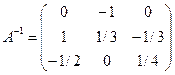 
.
Ранг матрицы. Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы. Ранг матрицы А обозначается rang(A) или r(A).
Из определения следует: а) ранг матрицы 
не превосходит меньшего из ее размеров, т.е. r(А) меньше или равен минимальному из чисел m или n; б) r(A)=0 тогда и только тогда, когда все элементы матрицы А равны нулю; в) для квадратной матрицы n-го порядка r(A)=n тогда и только тогда, когда матрица А - невырожденная.
Пример: вычислить ранги матриц:
.
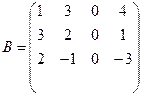Ответ: r(A)=1. Ответ: r(A)=2.
Назовем элементарными преобразованиями матрицы следующие:
1) Отбрасывание нулевой строки (столбца).
2) Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.
3) Изменение порядка строк (столбцов) матрицы.
4) Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
5) Транспонирование матрицы.
Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
Примеры: Вычислить матрицу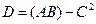 
, где
; 
; 
Ответ: 
.
Пример: Вычислить матрицу 
, где
; 
; 
; E – единичная матрица.
Ответ: 
.
Пример: Вычислить определитель матрицы
.
Ответ: 160.
Пример: Определить, имеет ли матрица А обратную, и если имеет, то вычислить ее:
.
Ответ: 
.
Пример: Найти ранг матрицы
.
Ответ: 2.
2.4.2. Системы линейных уравнений.
Система m линейных уравнений с n переменными имеет вид:
,
где , 
- произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами уравнений. Решением системы уравнений называется такая совокупность n чисел (
), при подстановке которых каждое уравнение системы обращается в верное равенство.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Теорема Крамера: Пусть - определитель матрицы А, составленной из коэффициентов при переменных “х”, а 
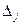- определитель матрицы, получаемой из матрицы А заменой j-го столбца этой матрицы столбцом свободных членов. Тогда, если 
, то система имеет единственное решение, определяемое по формулам: 
(j=1, 2, …, n). Эти уравнения получили названия формул Крамера.
Пример. Решить системы уравнений по формулам Крамера:
Ответы: (4, 2, 1). (1, 2, 3) (1, -2, 0)
Метод Гаусса – метод последовательного исключения переменных, заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних по номеру переменных, находятся все остальные переменные.
Пример: Решить системы уравнений методом Гаусса.
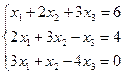
Ответы: (1, 1, 1). (1, -1, 2, 0). (1, 1, 1).
Для совместных систем линейных уравнений верны следующие утверждения:
· если ранг матрицы совместной системы равен числу переменных, т.е. r = n, то система уравнений имеет единственное решение;
· если ранг матрицы совместной системы меньше числа переменных, т.е. r<n, то система неопределенная и имеет бесконечное множество решений.
2.4.3. Технология выполнения операций над матрицами в среде EXCEL.
Рассмотрим некоторые аспекты работы с табличным процессором Excel, которые позволяют упростить расчеты, необходимые для решения оптимизационных задач. Табличный процессор – это программный продукт, предназначенный для автоматизации обработки данных табличной формы.
Работа с формулами. В программах электронных таблиц формулы служат для выполнения множества разнообразных расчетов. С помощью Excel можно быстро создать формулу. Формула состоит из трех основных частей:
- знак равенства;
- совокупность значений или ссылки на ячейки, с которыми выполняются расчеты;
- операторы.
Использование в формулах функций. Чтобы облегчить ввод формул, можно воспользоваться функциями Excel. Функции – это встроенные в Excel формулы. Для активизации той или иной формулы следует нажать кнопки Вставка, Функции. В появившемся окне Мастер функций слева содержится перечень типов функций. После выбора типа справа будет помещен список самих функций. Выбор функций осуществляется щелчком клавиши мыши на соответствующем названии.
При выполнении операций над матрицами, решении систем линейных уравнений, решении оптимизационных задач можно применять следующие функции Excel:
- МУМНОЖ - умножение матриц;
- ТРАНСП - транспонирование матрицы;
- МОПРЕД - вычисление определителя матрицы;
- МОБР - вычисление обратной матрицы.
Кнопка 
находится на панели инструментов. Функции для выполнения операций с матрицами находятся в категории Математические.
Умножение матриц с помощью функции МУМНОЖ. Функция МУМНОЖ возвращает произведение матриц (матрицы хранятся в массивах 1 и 2). Результатом является массив с таким же числом строк, как массив 1, и с таким же числом столбцов, как массив 2.
Пример. Найти произведение двух матриц А и В в среде Excel (см. рис 2.9):
; 
.
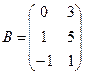- Введите матрицы А в ячейки А2:C3 и В в ячейки E2:F4.
- Выделите диапазон ячеек для результата умножения – H2:I2.
- Введите формулу умножения матриц =МУМНОЖ(A2:C3, E2:F4).
- Нажмите клавиши CTRL+SHIFT+ENTER.
Вычисления обратной матрицы с помощью функции МОБР.
Функция МОБР возвращает обратную матрицу для матрицы, хранящейся в массиве. Синтаксис: МОБР(массив). На рис. 2.10 приведено решение примера в среде Excel.
Пример. Найти матрицу, обратную к данной:
.
Рисунок 2.9. Исходные данные для умножения матриц.
Рисунок 2.10. Исходные данные для вычисления обратной матрицы.