Решение систем линейных уравнений методом

обратной матрицы и по формулам Крамера*

Рассмотрим систему n линейных уравнений с n неизвестными:

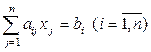. (2.3.1)

Запишем эту систему в матричном виде:

, (2.3.2)

где 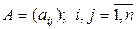– квадратная матрица порядка n, – столбец свободных членов высоты n, а X – неизвестная матрица.

Данное матричное уравнение относится к первому типу матричных уравнений 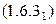и его решение, при условии, что , находится по формуле:

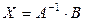. (2.3.3)

Этот способ решения системы (2.3.1) называется методом обратной матрицы.

Пример 2.3.1. Решить систему методом обратной матрицы:

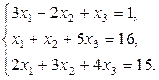
Решение.

Составим матрицы A, X и B для данной системы:

Найдем определитель матрицы А:

.

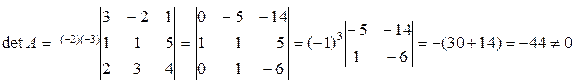Следовательно, согласно замечанию 2.2.1, система определенная; ее можно решать методом обратной матрицы. Найдем матрицу по формуле (1.6.2). Для этого вычислим алгебраические дополнения элементов матрицы А:

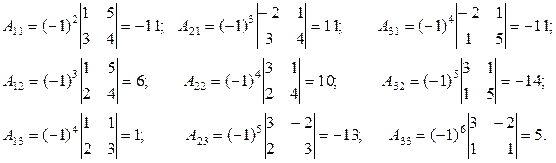
Таким образом,

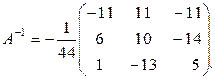
Подставляя и В в (2.3.3), находим:

 

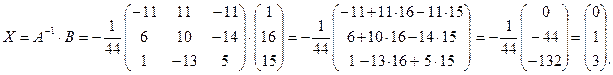
Ответ: .

Формулу (2.3.3), учитывая (1.6.2), можно переписать в виде: 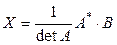. Умножая матрицы, находящиеся в правой части, по правилу (1.2.3) и используя определение равенства матриц (1.1.2), получим

, (2.3.4)

или в окончательной форме имеем:

 

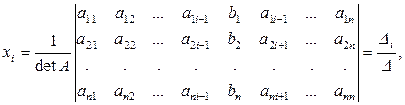(2.3.5)

 

где 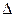– определитель матрицы А, а () – определитель матрицы, полученной из А заменой ее i -го столбца столбцом свободных членов 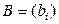. Для проверки, если разложить определитель по i -му столбцу (см. теорему 1.3.1), то получится выражение, стоящее в числителе (2.3.4). Таким образом, справедлива следующая теорема.

Теорема 2.3.1 (Правило Крамера). Если определитель матрицы системы 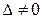, то существует единственное решение системы линейных уравнений (2.3.1), определяемое формулами (2.3.5).

Замечание 2.3.1. В частности, если система линейных уравнений (2.3.1) однородная и имеет 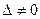, то она обладает единственным нулевым решением.

Замечание 2.3.2. Если определитель системы и при этом а) хотя бы один из , то система несовместная; b) все , то имеет место неопределенность, т.е. система либо несовместная, либо имеет бесконечное множество решений.

Пример 2.3.2. Приведем пример систем, у которых определитель системы и при этом все

a) 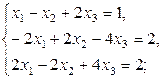b)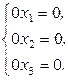

Несложно убедиться, что в первой системе

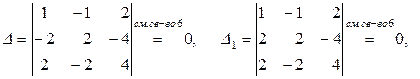
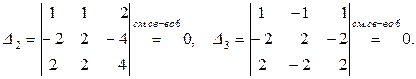
Система а) не имеет решения, так как первое и второе уравнения системы противоречивы.

Система b) у которой также все определители равны нулю, напротив, имеет бесконечное множество решений , где .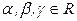

Пример 2.3.3. Систему из примера 2.3.1 решить методом Крамера.

Определитель 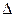системы уже найден, осталось вычислить определител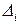и при .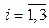

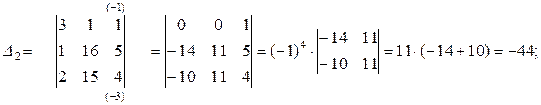
Подставляя значения определителей в формулы (2.3.5), найдем решение системы:

Ответ: .

 

Замечание 2.3.3. Решение системы (2.3.1) не зависит от выбранного способа.

В общем случае метод Крамера используется для систем, у которых количество уравнений совпадает с количеством неизвестных. Однако, используя несложный «приём», метод Крамера можно распространить и на произвольные системы.

Пример 2.3.4. Решить систему уравнений

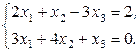
Решение.

Найдем ранги матриц

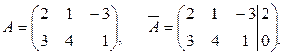
Здесь rangA=rang 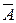= 2, так как среди миноров 2-го порядка этих матриц есть отличные от нуля, например , а миноров 3-го порядка нет. По теореме 2.2.1 система совместна. Оставляя переменные 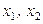слева, перенесем переменные 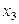вправо. Формально, получим систему, у которой количество уравнений совпадает с количеством неизвестных, т.е.

Решая систему методом Крамера, найдем

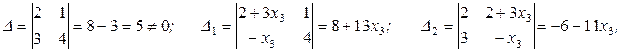
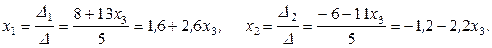
Полагая , где , получаем решения системы: .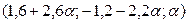

Ответ: , .

 

 

§4. Метод Гаусса* решения систем линейных уравнений

Для практического решения систем с большим числом уравнений и неизвестных описанные выше методы обратной матрицы и Крамера неудобны. В случае же, когда число уравнений в системе не совпадает с количеством неизвестных, матричный метод вообще применять нельзя. Универсальным способом решения систем линейных уравнений является метод Гаусса, в основе которого лежит принцип последовательного исключения неизвестных.

Рассмотрим систему (2.1.1):

 

 

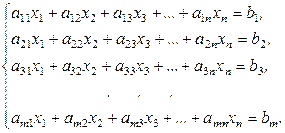
Определение 2.4.1. Элементарными преобразованиями системы называются следующие преобразования: 1) перестановка уравнений системы местами; 2) умножение некоторого уравнения системы на отличное от нуля число; 3) прибавление к одному уравнению другого, умноженного на любое число; 4) вычеркивание нулевой строки (исключение уравнений, тождественно удовлетворяющихся любыми значениями неизвестных).

Несложно убедиться, что при использовании элементарных преобразований от системы переходят к системе, эквивалентной данной.

Элементарные преобразования системы удобно производить над строками ее расширенной матрицы.

Опишем стандартный способ построения и записи эквивалентных систем. Предположим, что первым в системе (2.1.1) стоит уравнение, в котором коэффициент 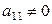. Если это не так, то этого всегда можно добиться перестановкой уравнений или неизвестных. К каждой строке матрицы 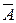, начиная со второй, прибавим почленно первую строку, умноженную на , соответственно. Тогда в первом столбце все элементы, за исключением , будут равны нулю. То есть, исключив первое неизвестное из всех уравнений, начиная со второго, мы получаем эквивалентную систему с расширенной матрицей вида

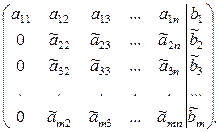
Если в получившейся системе вторая переменная присутствует, начиная со второй строки, хотя бы в одном уравнении, то мы можем применить прежний приём и исключить вторую переменную из всех уравнений, кроме первых двух.

Повторяя описанную процедуру необходимое число раз, приводим расширенную матрицу системы к следующему виду:

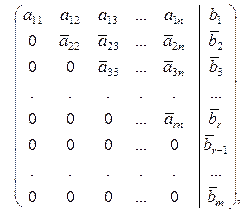(2.4.1)

где .

Если в (2.4.1) среди свободных членов 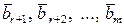есть отличные от нуля, то система не имеет решения. Действительно, в этом случае 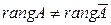, а согласно теореме 2.2.1 это и означает, что система несовместна. Если все 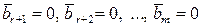, то последние (m–r) уравнений системы обращаются в тождества 0=0 и могут быть отброшены. В зависимости от вида матрицы (2.4.1) возможны два случая:

a) матрица (2.4.1) приведена к треугольной форме (r=n). В этом случае система, согласно теореме 2.2.2, имеет единственной решение. Для того чтобы его найти, нужно от матрицы перейти к системе, при этом удобно последнюю строку расширенной матрицы записывать в первую строку системы, т.е.

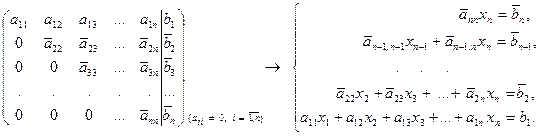(2.4.1')

 

Решая систему (2.4.1') последовательно сверху вниз, находим весь набор , составляющий решение.

b) матрица (2.4.1) приведена к трапециевидной форме (r<n). В этом случае система, согласно теореме 2.2.3, имеет бесконечное множество решений. Запишем систему, соответствующую полученной матрице:

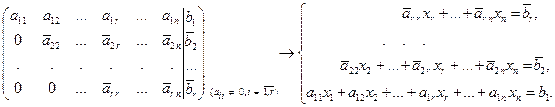(2.4.2')

Все переменные делим на две части: основные (базисные) и свободные (небазисные). Основные выбираются так, чтобы их было столько же, сколько уравнений, и чтобы коэффициенты при них образовывали отличный от нуля определитель, т.е. базисный минор. Их выбор неоднозначен, однако, по-возможности, в качестве основных берут первые r переменных. Все остальные переменные (их количество n–r) объявляются свободными и переносятся к свободным членам вправо. Относительно основных переменных система будет иметь треугольный вид. Последовательно решая уравнения системы, мы получим, что все основные переменные будут выражаться через свободные. Такое решение называется общим. Если придавать свободным переменным различные числовые значения, то будем получать различные частные решения.

Замечание 2.4.1. Описанная выше схема исключения неизвестных для нахождения решений систем линейных уравнений есть суть метода Гаусса. При решении системы по методу Гаусса нет необходимости заранее знать, совместна она или нет. Это определяется в процессе работы.

Пример 2.4.1. Решить системы методом Гаусса:

a) 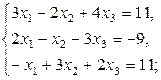b)

Решение:

a)

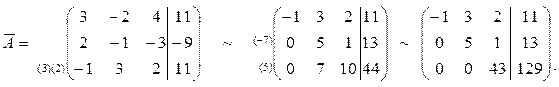
Матрица приведена к треугольной форме (r=n=3). Следовательно, система имеет единственное решение, которое находим из системы:

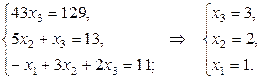
Ответ:(1, 2, 3).

b)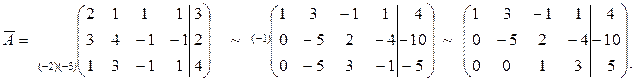

 

Имеем . Следовательно, система совместна. Число неизвестных в системе n=4, r<n,т.е. система приведена к трапециевидной форме.Таким образом, она имеет бесконечное множество решений. Для того чтобы их найти, определимся, какие переменные мы будем считать основными, а какие свободными. Для этого найдем один из базисных миноров матрицы системы, например, минор 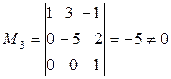. Переменные , коэффициенты при которых составляют , будем считать основными (базисными), а остальные – свободными (небазисными). Далее записываем систему, соответствующую последней матрице. Последовательно выражая базисные переменные через небазисные, находим общее решение системы

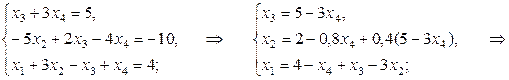
Пусть , тогда множество наборов вида является решением системы.

Ответ: , .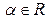