Савельев И.В. Курс общей физики

Механика представляет собой учение о простейшей форме движении материи, которое состоит в перемещении тел или их частей друг относительно друга.

Перемещение тел мы наблюдаем повседневно в обыденной жизни. Отсюда следует наглядность механических представлений. Этим же объясняется то, что из всех естественных наук механика прежде других получила широкое развитие.

Движение одного и того же тела относительно различных тел может иметь разный характер. Если, например тело 1 относительно нас покоится, а тела 2 и 3 движутся в одну и ту же сторону с одинаковой скоростью, то тело 3 перемещается относительно тела 1, однако покоится относительно тела 2. Поэтому для описания движения необходимо условиться, относительно какого другого тела (или группы неподвижных друг относительно друга тел) будет отсчитываться перемещение данного тела. Выбранное для этой цели тело (или группа тел) образует систему отсчета,

Практически для описания движения приходится связывать с телами, образующими систему отсчета, какую-либо систему координат, например декартову или прямоугольную систему координат.

Координаты тела позволяют определить его положение в пространстве. Однако движение происходит как в пространстве, так и во времени (пространство и время — неотъемлемые формы существования материи). Поэтому для описания движения необходимо также отсчитывать время. Это делается с помощью часов

Располагая координатной системой, связанной с выбранной системой отсчета, и часами, можно приступить к описанию движения тел.

Движение тел обычно происходит в условиях, когда на них действуют силы.

Действие этих сил наряду с тем, что определяет характер движения, вызывает также деформацию тел, т. е. изменение их размеров и формы. Очень часто деформации настолько незначительны, что ими можно пренебречь при описании движения тела. Тело, деформациями которого в условиях рассматриваемой задачи можно пренебречь, называется абсолютно твердым телом. Следует иметь в виду, что абсолютно твердых (т, е. совершенно недеформируемых) тел в природе не существует, Только пренебрежимо малая роль деформаций при движении тел в определенных условиях дает возможность рассматривать, их как абсолютно твердые.

Иногда при рассмотрении движения тел можно пренебречь их размерами. Это бывает в тех случаях, когда размеры тела во много раз меньше прочих размеров, с которыми приходится иметь дело в условиях данной задачи. Например, при определении пути, проходимого автомобилем при переезде из Ленинграда в Москву, размерами автомобиля вполне можно пренебречь.

Тело, размерами которого в условиях данной задачи можно пренебречь, называется материальной точкой. Вопрос о том, можно ли данное конкретное тело рассматривать как материальную точку или нет, зависит не от размеров самого тела, а от условий задачи. Одно и то же тело в одних случаях может быть сочтено за материальную точку, в других же — должно рассматриваться как протяженное тело. Так, например, при вычислении траектории, по которой Земля движется круг Солнца, Землю можно рассматривать как материальную точку. При рассмотрении же движения тел поверхности Земли она должна рассматриваться как протяженное тело.

Всякое движение твердого тела можно разложить на два основных вида движении — поступательное и вращательное.

Поступательное движение — это такое движение, в котором любая прямая, связанная с движущимся телом, остается параллельной самой себе (рис. 1).

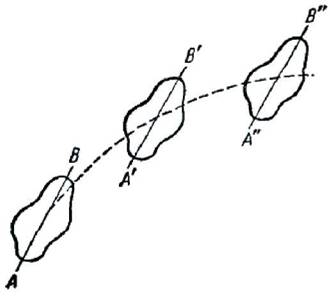
Рис.1

При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения (рис. 1).

Ось вращения может находиться вне тела (рис. 2)

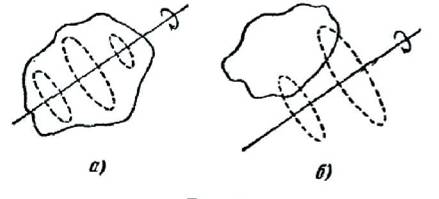
Рис.2

Поскольку, говоря о каком-либо теле как о материальной точке, мы отвлекаемся от его протяженности, понятие вращательного движения вокруг проходящего через него оси к такому телу неприменимо.

Механика подразделяется на три раздела: 1) кинематику, 2) статику и 3) динамику. Кинематика изучает движение тел вне зависимости от тех причин, которые обусловливают это движение, статика изучает тело равновесия тел и, наконец, динамика изучает движение тел в связи с теми-причинами (взаимодействиями между телами), которые обусловливают тот или иной характер движения. Поскольку равновесие есть частный случай движения, законы статики оказываются естественным следствием законов динамики.

Материальная точка при своем движении описывает некоторую линию. Эта линия называется траектория В зависимости от формы траектории различают прямолинейное движение, движение по окружности, кривое иней движение и т. д.

Пусть материальная точка (в дальнейшем мы для краткости будем говорить просто точка) переместилась вдоль некоторой траектории из точки 1 в точку 2 (рис. 3).

Рис. 3.

Расстояние от точки 1 до точки 2, отсчитанное вдоль траектории, представляет собой пройденный путь. Мы будем обозначать его буквой s.

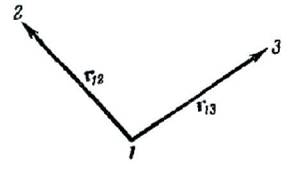
Отрезок прямой, проведенный из точки 1 в точку 2, называется перемещением. Обозначим его r₁₂. Перемещение характеризуется, кроме своей величины (равно длине отрезка r12), также и направлением. Действительно, рассмотрим два одинаковых по величине перемещения r12 и r13 (рис. 4). Несмотря на равенство длин этих отрезков, они явно представляют собой совершенно различные перемещения.

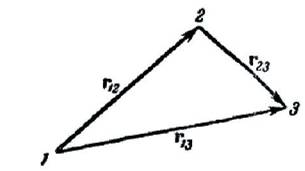
Величины, подобные перемещению, подчиняются правилу сложения, которое можно уяснить на следующем примере. Пусть точка совершает последовательно два перемещения: r₁₂ и r₂₃ (рис. 5). Суммой этих двух перемещений естественно назвать такое перемещение

r₁₃,которое приводит к тому же результату, что и первые два перемещения вместе.

Величины такого рода, как перемещение, т. е. характеризующиеся численным значением и направлением, а также складывающиеся по правилу, показанному на рис. 5, называются векторами. К числу векторов принадлежат скорость, ускорение, сила и ряд других величин.

Величины, для задания которых достаточно одного численного значения, называются скалярами. Примерами скаляров могут служить путь, время, масса и т, д.

Рис.4	Рис.5

Векторы принято обозначать буквами жирного шрифта. Например, вектор перемещения из точки 1 в точку 2 обозначается r₁₂. Та же буква обычного шрифта означает численное значение или, как говорят, модуль соответствующего вектора [1]. Для обозначения модуля пользуются также символом вектора, заключенным между двумя вертикальными черточками. Таким образом,

|A|=A=модулю вектора A,

|r₁₂|=r₁₂=модулю вектора r₁₂

Модуль вектора — скаляр, причем всегда положительный.

На чертежах векторы изображаются в виде прямолинейных отрезков со стрелкой на конце. Длина отрезка в установленном масштабе дает модуль вектора, а указанное стрелкой направление отрезка дает направление вектора.

Показанная на рис. 5 операция сложении векторов символически записывается следующим образом:

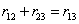
[1]При письме векторы обозначают буквами со стрелкой над ними (например, 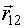). В этом случае та же буква без стрелки означает модуль вектора.