Постановка задач для уравнений параболического типа
Классическим примером уравнения параболического типа является уравнение теплопроводности (диффузии). В одномерном по пространству случае однородное (без источников энергии) уравнение теплопроводности имеет вид
(1)
Если на границах 
и 
заданы значения искомой функции 
в виде
, , (2)
, , (3)
т.е. граничные условия первого рода, и, кроме того заданы начальные условия
, 
, (4)
то задачу (1)-(4) называют первой начально-краевой задачей для уравнения теплопроводности (1).
В терминах теории теплообмена — распределение температуры в пространственно-временной области
a2 — коэффициент температуропроводности, а (2), (3) с помощью функций 
, 
задают температуру на границах и .
Если на границах и 
заданы значения производных искомой функции по пространственной переменной:
, , (5)
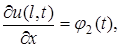
, , (6)
т.е. граничные условия второго рода, то задачу (1), (5), (6), (4) называют второй начально-краевой задачей для уравнения теплопроводности (1). В терминах теории теплообмена на границах в этом случае заданы тепловые потоки.
Если на границах заданы линейные комбинации искомой функции и ее производной по пространственной переменной:
, , (7)
, , (8)
т.е. граничные условия третьего рода, то задачу (1), (7), (8), (4) называют третьей начально-краевой задачей для уравнения теплопроводности (1). В терминах теплообмена граничные условия (7), (8) задают теплообмен между газообразной или жидкой средой с известными температурами 
на границе и 
на границе и границами расчетной области с неизвестными температурами 
, 
. Коэффициенты α, β – известные коэффициенты теплообмена между газообразной или жидкой средой и соответствующей границей.
Для пространственных задач теплопроводности в области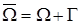 
первая начально-краевая задача имеет вид
(9)
Аналогично ставится вторая и третья начально-краевые задачи для пространственного уравнения (9). На практике часто ставятся начально-краевые задачи теплопроводности со смешанными краевыми условиями, когда на границах задаются граничные условия различных родов.
Основные определения и конечно-разностные схемы
Основные определения, связанные с методом конечных разностей, рассмотрим на примере конечно-разностного решения первой начально-краевой задачи для уравнения теплопроводности (1)-(4).
Согласно методу сеток в плоской области D строится сеточная область Dh, состоящая из одинаковых ячеек. При этом область Dh должна как можно лучше приближать область D. Сеточная область (то есть сетка) Dh состоит из изолированных точек, которые называются узлами сетки. Число узлов будет характеризоваться основными размерами сетки h: чем меньше h, тем больше узлов содержит сетка. Узел сетки называется внутренним, если он принадлежит области D, а все соседние узлы принадлежат сетке Dh. В противном случае он называется граничным. Совокупность граничных узлов образует границу сеточной области Г h.
Сетка может состоять из клеток разной конфигурации: квадратных, прямоугольных, треугольных и других. После построения сетки исходное дифференциальное уравнение заменяется разностным уравнением во всех внутренних узлах сетки. Затем на основании граничных условий устанавливаются значения искомого решения в граничных узлах. Присоединяя граничные условия сеточной задачи к разностным уравнениям, записанных для внутренних узлов, получаем систему уравнений, из которой определяем значения искомого решения во всех узлах сетки.
Нанесем на пространственно-временную область , 
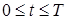конечно разностную сетку ωh,τ:
(10)
с пространственным шагом h=l/N и шагом по времени τ=T/K.
Рисунок 1 – Конечно-разностная сетка
Введем два временных слоя: нижний 
,на котором распределение искомой функции u(xj,tk), 
, известно (при к = 0 распределение определяется начальным условием (4) u(xj,tk)=ψ(xj)), и верхний временной слой tk+1=(k+1) τ, на котором распределение искомой функции u(xj,tk+1), .
Сеточной функцией задачи (1)-(4) называют однозначное отображение целых аргументов j,k в значения функции 
.
На введенной сетке вводят сеточные функции 
, 
первая из которых известна, вторая подлежит определению. Для определения в задаче (1)-(4) заменяют (аппроксимируют) дифференциальные операторы отношением конечных разностей (более подробно это рассматривают в разделах численных методов «Численное дифференцирование»), получают
, (11)
, (12)
Подставляя (11), (12) в задачу (1)-(4), получим явную конечно-разностную схему для этой задачи в форме
(13)
В каждом уравнении этой задачи все значения сеточной функции известны, за исключением одного, 
, которое может быть определено явно из соотношений (13). В соотношения (13) краевые условия входят при значениях j=1 и j=N-l, a начальное условие – при k = 0.
Если в (12) дифференциальный оператор по пространственной переменной аппроксимировать отношением конечных разностей на верхнем временном слое:
, (14)
то после подстановки (11), (14) в задачу (1)-(4) получим неявную конечно-разностную схему для этой задачи:
(15)
Теперь сеточную функцию 
на верхнем временном слое можно получить из решения (15) с трехдиагональной матрицей. Эта СЛАУ в форме, пригодной для использования метода прогонки, имеет вид
где
;
;
, ;
;
;
;
.
Шаблоном конечно-разностной схемы называют ее геометрическую интерпретацию на конечно-разностной сетке. На рисунке приведены шаблоны для явной и неявной конечно-разностных схем при аппроксимации задачи.
Рисунок 2 - Шаблон явной конечно-разностной схемы для уравнения теплопроводности
Рисунок 3 - Шаблон неявной конечно-разностной схемы для уравнения теплопроводности
В случае явных схем значения функции в узле очередного слоя можно найти, зная значения в узлах предыдущих слоев. В случае неявных схем для нахождения значений решения в узлах очередного слоя приходится решать систему уравнений. Для проведения вычислений самой простой схемой оказывается первая: достаточно на основании начального условия найти значения функции в узлах слоя 
, чтобы в дальнейшем последовательно определять значения решения в узлах слоев 
и т.д. В случае второй схемы, которая является неявной, обязательно приходится решать систему уравнений для нахождения решения сеточной задачи. В любом случае согласно методу сеток будем иметь столько уравнений, сколько имеется неизвестных (значения искомой функции в узлах). Число неизвестных равно числу всех узлов сетки. Решая систему уравнений, получаем решение поставленной задачи.
Разрешимость этой системы для явных схем вопросов не вызывает, так как все действия выполняются в явно определенной последовательности. В случае неявных схем разрешимость системы следует исследовать в каждом конкретном случае. Важным вопросом является вопрос о том, на сколько найденные решения хорошо (адекватно) отражают точные решения, и можно ли неограниченно сгущая сетку (уменьшая шаг по осям) получить приближенные решения, сколь угодно близкие к точным решениям? Это вопрос о сходимости метода сеток.
На практике следует применять сходящиеся разностные схемы, причем только те из них, которые являются устойчивыми, то есть при использовании которых небольшие ошибки в начальных или промежуточных результатах не приводят к большим отклонениям от точного решения. Всегда следует использовать устойчивые разностные схемы, проводя соответствующие исследования на устойчивость. Явные схемы просты для организации вычислительного процесса, но имеют один весьма весомый недостаток: для их устойчивости приходится накладывать сильные ограничения на сетку. Неявные схемы свободны от этого недостатка, но есть другая трудность – надо решать системы уравнений большой размерности, что на практике при нахождении решения сложных уравнений в протяженной области с высокой степенью точности может потребовать больших объемов памяти ЭВМ и времени на ожидание конечного результата. К счастью, прогресс не стоит на месте и уже сейчас мощности современных ЭВМ вполне достаточно для решения поставленных перед ними задач.
Вопрос устойчивости будет рассмотрен далее.
Аппроксимация
Из определения порядка аппроксимации ясно, что чем выше порядок аппроксимации, тем лучше конечно-разностная схема приближается к дифференциальной задаче. Это не означает, что решение по разностной схеме может быть так же близко к решению дифференциальной задачи, так как разностная схема может быть условно устойчивой или абсолютно неустойчивой вовсе.
Для нахождения порядка аппроксимации используется аппарат разложения в ряды Тейлора точных (неизвестных, но дифференцируемых) решений дифференциальной задачи в узлах сетки (подчеркнем: значения сеточной функции uh дискретны, следовательно, не дифференцируемы и поэтому не разлагаются в ряды Тейлора).