Моделирование периодических колебаний

Построение аддитивной модели временного ряда. Обратимся к данным о производстве яиц в Тамбовской области за 2014-2017 гг. по кварталам (табл. 5).

Было показано, что данный временной ряд содержит сезонные колебания, т.к. количество произведенных яиц во второй и третий кварталы выше, чем в четвертый и первый. Рассчитаем компоненты аддитивной модели временного ряда.

Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:

1.1. Просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объемы производства яиц (гр. 5).

1.2. Разделив полученные суммы на 4, найдем скользящие средние (гр. 6). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.

1.3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних - центрированные скользящие средние (гр. 7).

1.4. Для определения сезонной компоненты найдем разницу между фактическими уровнями и центрированными четырех скользящими средними (гр.8= гр.4-гр.7).

Таблица 5 - Производство яиц в Тамбовской области

за 2014-2017 гг по кварталам (млн. шт).

Год	квартал	t	y_t	Четырехчленные скользящие средние (нецентрированные)	Четырехчленные скользящие средние (центрированные)	Оценка сезонной компоненты

	I
II			10437,75
III			10518,25
IV			10586,25	10552,25	-548,25
	I			10593,25	10589,75	-703,75
II				10618,13	728,875
III				10684,5	451,5
IV			10781,75	10753,88	-550,875
	I			10798,75	10790,25	-572,25
II			10889,5	10844,13	725,875
III			10960,75	10925,13	278,875
IV				10999,38	-433,375
	I			11153,75	11095,88	-592,875
II			11222,75	11188,25	690,75
III
IV

Шаг 2. Оценки расчета значений сезонной компоненты S используем для расчета в таблице 6. Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты S_t. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.

Для данной модели имеем:

-622,9583333+715,1666667+453,4583333-510,8333333= 34,83333333

Корректирующий коэффициент: k=34,83333333/4=8,708333333

Рассчитаем скорректированные значения сезонной компоненты:

-622,9583333-8,708333333 =-631,6666667

715,1666667-8,708333333= 706,4583333

453,4583333-8,708333333=444,75

-510,8333333-8,708333333=-519,5416667

Проверим равенство нулю суммы значений сезонной компоненты

-631,6666667+ 706,4583333 + 444,75 -519,5416667 = 0

Таблица 6 - Определим скорректированное значение

сезонной компоненты

Год	квартал
I	II	III	IV
				-548,25
	-703,75	728,875	451,5	-550,875
	-572,25	725,875	278,875	-433,375
	-592,875	690,75
Всего	-1868,875	2145,5	1360,375	-1532,5
средняя оценка сезонной компоненты для i квартала, S	-622,9583333	715,1666667	453,4583333	-510,8333333
Скорректированная сезонная компонента, S	-631,6666667	706,4583333	444,75	-519,5416667

Шаг 3. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины Т + Е = Y – S (гр. 6 таблицы 10). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.

Шаг 4. Определим компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда (T + E) с помощью линейного тренда. Результаты аналитического выравнивания следующие:

T = 10236,98333 - 66,03137255t

Подставляя в это уравнение значения t = 1, 2,..., 16, найдем уровни T для каждого момента времени (гр. 7).

Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням T значения сезонной компоненты для соответствующих кварталов (гр. 8).

На одном графике отложим фактические значения уровней временного ряда и теоретические, полученные по аддитивной модели (рис. 4). Полученные данные показывают полное совпадение эмпирических и теоретических уровней. Для оценки качества построенной модели применим сумму квадратов полученных абсолютных ошибок.

Следовательно, можно сказать, что аддитивная модель объясняет 98,3% общей вариации уровней временного ряда производства яиц в Тамбовской области по кварталам за 4 года.

Таблица 7 - Расчет теоретических уровней для аддитивной модели

Год квартал t y_t Si y_t-Si Т утеор=T+S E=y_t - (T+S) E2 (y_t-уср)^2

I -631,6666667 10195,6667 10303,01 9671,348039 -107,3480392 11523,6 1523373,06

II 706,4583333 10368,5417 10369,05 11075,50441 -0,504411758 0,254431 76590,5625

III 444,75 10663,25 10435,08 10879,82745 228,172549 52062,71 95945,0625

IV -519,5416667 10523,5417 10501,11 9981,567157 22,43284314 503,2325 630833,063

I -631,6666667 10517,6667 10567,14 9935,473529 -49,4735294 2447,63 832200,063

II 706,4583333 10640,5417 10633,17 11339,6299 7,370098047 54,31835 301126,563

III 444,75 10691,25 10699,2 11143,95294 -7,952941202 63,24927 114075,063

IV -519,5416667 10722,5417 10765,23 10245,69265 -42,69264705 1822,662 354322,563

I -631,6666667 10849,6667 10831,27 10199,59902 18,4009804 338,5961 336690,063

II 706,4583333 10863,5417 10897,3 11603,75539 -33,75539215 1139,426 595598,063

III 444,75 10759,25 10963,33 11408,07843 -204,0784314 41648,01 164633,063

IV -519,5416667 11085,5417 11029,36 10509,81814 56,18186275 3156,402 53940,0625

I -631,6666667 11134,6667 11095,39 10463,72451 39,27549021 1542,564 87172,5625

II 706,4583333 11172,5417 11161,42 11867,88088 11,11911766 123,6348 1168020,56

III 444,75 11222,25 11227,45 11672,20392 -5,203921592 27,0808 754726,563

IV -519,5416667 11361,5417 11293,49 10773,94363 68,05637256 4631,67 1914,0625

Итого -3,99999E-07 5,45697E-12

Рис. 4 Эмпирические и теоретические уровни ряда (аддитивная модель) по производству яиц в Тамбовской области по кварталам за 2014-2017 годы, (млн.шт)

Шаг 6. Прогнозирование по аддитивной модели. Предположим, что по нашему примеру необходимо дать прогноз об общем объеме производстве яиц на I и II кварталы 2018 года. Прогнозное значение F_tуровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда:

T = 10236,98333 - 66,03137255t

получим

T₁₇ =10236,98333 - 66,03137255*17 = 9114,449997 (млн. шт.)

T₁₈ =10236,98333 - 66,03137255*18 = 9048,418624 (млн. шт)

Значения сезонных компонент за соответствующие кварталы равны S₁=-631,6666667, а S₂=706,4583333. Таким образом, прогноз производства яицв Тамбовской области составит на:

I квартал 2018 года У= Т₁₇+S₁=9114,449997 –631,6666667 = 8482,78333 млн. шт

II квартал 2018 года У= Т₁₈+S₂=9048,418624 +706,4583333= 9754,876957 млн.шт

Проверим гипотезу о наличии автокорреляции в остатках для аддитивной модели нашего временного ряда (табл. 8).

Таблица 8 – Расчет автокореляции в остатках

(критерий Дарбина-Уотсона)

Год квартал t y_t Е Еt-1 (Еt-1)^2 E^2

I -9564

II -11075 1,50471E+16

III -11108 1,52273E+16

IV -10004 1,0018E+16

I -9886 9,55367E+15

II -11347 1,65806E+16

III -11136 1,53814E+16

IV -10203 1,08392E+16

I -10218 1,09031E+16

II -11570 1,79229E+16

III -11204 1,57605E+16

IV -10566 1,24659E+16

I -10503 1,21713E+16

II -11879 1,99156E+16

III -11667 1,85315E+16

IV -10842 1,38203E+16

сумма -172772 2,14138E+17

Фактическое значение критерия Дарбина-Уотсона для данной модели составляет:

d =11558524/876126375= 0,013192759

Сформулируем гипотезы: Н₀ - в остатках нет автокорреляции; Н₁ – в остатках есть положительная автокорреляция; Н₁ - в остатках есть отрицательная автокорреляция. Зададим уровень значимости а = 0,05. По таблице значений критерия Дарбина-Уотсона определим для числа наблюдений n = 16 и числа независимых параметров модели к = 1 (мы рассматриваем только зависимость от времени t) критические значения d_L = 1,1 и d_y = 1,37. Фактическое значение d-критерия Дарбина-Уотсона не попадает в интервал d_y < d < 4 — d_y (1,1<0,013<1,37). Следовательно, гипотеза Н₀ говорит присутствии автокорреляции в остатках.

Далее перейдем к построению мультипликативной модели.

Шаг 1 первый совпадает с построением аддитивной модели за исключением оценки сезонной компоненты (гр.8 таблица 9), которая определяется, как частное от деления фактических уровней ряда на центрированные скользящие средние.

Шаг 2 Найдем средние за каждый квартал оценки сезонной компоненты S_t. И отразим их в таблице 10. Так же как и в аддитивной модели считается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле.

Таблица 9 - Производство яиц

в Тамбовской области

за 2014-2017 гг по кварталам (млн. шт).

Год квартал t y_t Четырехчленные скользящие суммы Четырехчленные скользящие средние (нецентрированные) Четырехчленные скользящие средние (центрированные) Оценка сезонной компоненты

I

II 10437,75

III 10518,25 1,060125978

IV 10586,25 10552,25 0,948044256

I 10593,25 10589,75 0,933544229

II 10618,125 1,068644417

III 10684,5 1,042257476

IV 10781,75 10753,875 0,948774279

I 10798,75 10790,25 0,946966011

II 10889,5 10844,125 1,066937166

III 10960,75 10925,125 1,025526024

IV 10999,375 0,960600034

I 11153,75 11095,875 0,946567981

II 11222,75 11188,25 1,061738878

III

IV

Таблица 10 - Определим скорректированное значение

сезонной компоненты

Год квартал

I II III IV

1,060125978 0,948044256

0,9335442 1,068644417 1,042257476 0,948774279

0,946966 1,066937166 1,025526024 0,960600034

0,946568 1,061738878

Всего 2,82707822 3,197320461 3,127909478 2,857418569

средняя оценка сезонной компоненты для i квартала, S 0,94235941 1,065773487 1,042636493 0,952472856

Скорректированная сезонная компонента, S 0,94159619 1,064910313 1,041792057 0,951701444

В нашем случае число периодов одного цикла равно 4.

Имеем 0,94235941+1,065773487+1,042636493+0,952472856=4,003242243

Определим корректирующий коэффициент:

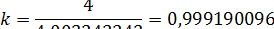
Скорректированные значения сезонной компоненты S получаются умножением ее средней оценки на корректирующий коэффициент:

0,94235941∙0,999190096= 0,941596186

1,065773487∙ 0,999190096= 1,064910313

1,042636493∙0,999190096= 1,041792057

0,952472856∙ 0,999190096=0,951701444

Проверяем условие соответствия 4 значений сезонной компоненты:

0,941596186+1,064910313 +1,041792057 +0,951701444 = 4

Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате получим величины (гр. 6 табл. 11), которые содержат только тенденцию и случайную компоненту.

Таблица 11 - Расчет теоретических уровней ряда

для мультипликативной модели

Год квартал t y_t Si Yt/S Т утеор=T*S E=yt/(T*S) (yt-TS)^2

I 0,941596186 10157,22041 10296,38473 9695,036595 0,986484 17170,59

II 1,064910313 10399,93685 10363,28166 11035,96551 1,003537 1523,692

III 1,041792057 10662,39652 10430,17858 10866,0772 1,022264 58526,64

IV 0,951701444 10511,69992 10497,07551 9990,081924 1,001393 193,7128

I 0,941596186 10499,19291 10563,97243 9946,996155 0,993868 3720,531

II 1,064910313 10655,35742 10630,86936 11320,92241 1,002303 680,0406

III 1,041792057 10689,27328 10697,76629 11144,84794 0,999206 78,28607

IV 0,951701444 10720,79911 10764,66321 10244,74553 0,995925 1742,689

I 0,941596186 10851,78567 10831,56014 10198,95572 1,001867 362,6848

II 1,064910313 10864,76473 10898,45706 11605,87932 0,996909 1287,325

III 1,041792057 10754,54543 10965,35399 11423,61868 0,980775 48232,37

IV 0,951701444 11102,22125 11032,25091 10499,40913 1,006342 4434,344

I 0,941596186 11154,46319 11099,14784 10450,91528 1,004984 2712,818

II 1,064910313 11154,93001 11166,04477 11890,83622 0,999005 140,0961

III 1,041792057 11198,97193 11232,94169 11702,38943 0,996976 1252,412

IV 0,951701444 11392,22816 11299,83862 10754,07273 1,008176 7731,204

Итого 149789,4

Шаг 4. Определим компоненту T в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни Y/S. В результате получим уравнение тренда:

Т=10229,48781- 66,89692568t

Подставляя в это уравнение значения t = 1, 2,..., 16, найдем уровни T для каждого момента времени (гр. 7).

Шаг 5. Найдем уровни ряда, умножив значения Tна соответствующие значения сезонной компоненты (гр. 8). На одном графике откладываем фактические значения уровней временного ряда и теоретические, полученные по мультипликативной модели (рис. 5).

Расчет ошибки в мультипликативной модели производится по формуле:

E = У/(T*S)

Для сравнения мультипликативной модели и других моделей временного ряда можно, по аналогии с аддитивной моделью, использовать сумму квадратов абсолютных ошибок (y_t - T S)²:

Сравнивая показатели детерминации аддитивной ( и мультипликативной моделей (, делаем вывод, что аддитивная модель чуть лучше аппроксимируют исходные данные.

Рис. 5 Эмпирические и теоретические уровни ряда (мультипликативная модель) по производству яиц в Тамбовской области по кварталам за 2014-2017 годы, (млн. шт)

Шаг 6. Прогнозирование по мультипликативной модели. Предположим, что по нашему примеру необходимо дать прогноз об общем объеме производства яиц на I и II кварталы 2018 года. Прогнозное значение F_tуровня временного ряда в мультипликативной модели есть произведение трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда:

Т=10229,48781- 66,89692568t

Получим

Т₁₇=10229,48781- 66,89692568*17 = 9092,240073 млн.шт

Т₁₈=10229,48781- 66,89692568*18 = 9025,343148 млн.шт

Значения сезонных компонент за соответствующие кварталы равны S₁=0,941596186, а S₂=1,064910313. Таким образом, прогноз производства молока в Тамбовской области составит на:

I квартал 2018 года У= Т₁₇∙S₁= 9092,240073 ∙0,941596186 = 8561,218575 млн.шт

II квартал 2018 года У= Т₁₈∙S₂=9025,343148 ∙1,064910313 =9611,180996 млн.шт

Таким образом, мультипликативная модель дает приблизительно такие же прогнозные данные как и аддитивная модель.

Моделирование сезонных колебаний с помощью гармонического анализа.

у_t = а₀ + a₁cost + bsint.

При k = 2 соответственно

; ;

Параметры уравнения выравненных уровней, определяемых рядом Фурье, находят по способу наименьших квадратов: у_t = 219,5- 52,703cost +5,21383sint.

Таблица 12 Расчет параметров гармоники ряда Фурье

Месяцы Изделия три-котажные или вязанные, тыс. шт t cost sint уcost уsint уt

Январь 104,8 104,8

Февраль 129,8 0,87 0,50 112,926 64,9

Март 252,7 0,50 0,87 126,35 219,849

Апрель 216,8 0,00 1,00 216,8

Май 298,6 -0,50 0,87 -149,3 259,782

Июнь 247,5 -0,87 0,50 -215,33 123,75

Июль 243,2 -1,00 0,00 -243,2

Август 245,9 -0,87 -0,50 -213,93 -122,95

Сентябрь 236,5 -0,50 -0,86 -118,25 -203,39

Октябрь 249,9 0,00 -1,00 -249,9

Ноябрь 198,4 0,50 -0,87 99,2 -172,61

Декабрь 209,9 0,86 -0,50 180,514 -104,95

Сумма -0,01 0,00 -316,22 31,283

На рисунке 6 представлены фактические и теоретические уровни ряда динамики Фурье.

Рис. 6 Фактические и теоретические уровни ряда динамики Фурье производства изделий трикотажных или вязанных по Тамбовской области за 2017 год в (тыс. шт).

Моделирование периодических колебаний

Поиск по сайту