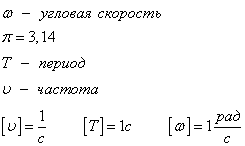Тема: Равномерное движение точки по окружности.
Дата: 15.10.2010 г.
Студенты должны знать: понятие «криволинейное движение»; физические величины, которые характеризуют это движение.
Студенты должны уметь: использовать свои знания для решения соответствующих задач; объяснять процессы, которые происходят при равномерном движении тела по окружности.
План
1. Равномерное движение материальной точки окружности. Линейная скорость.
2. Угловая скорость.
3. Период и частота.
4. Центростремительное ускорение.
Равномерное движение материальной точки окружности. Линейная скорость.
Движение тела по окружности является частным случаем криволинейного движения.
Движение, при котором материальная точка движется по окружности с постоянной скоростью, называют равномерным движением по окружности.
Допустим, что материальная точка движется равномерно по окружности и в момент t1 находится в положении А (рис. 1), а в момент t2 точка заняла положение В. Радиус, проведенный из центра окружности к материальной точке, за это время описал угол φ, который называют угловым перемещением.
Угловое перемещение в международной системе единиц выражают в радианах.
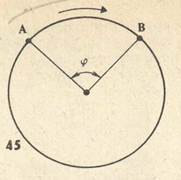
Рисунок 1.
Радиан – центральный угол между двумя радиусами окружности, длина дуги между двумя радиусами окружности. Т.е. наряду с вектором перемещения Δl удобно рассматривать угловое перемещение Δφ (или угол поворота), измеряемое в радианах. Длина дуги связана с углом поворота соотношением
Δl = R Δφ.
При малых углах поворота Δl ≈ Δs.
Допустим что материальная точка равномерно движется по окружности радиусом R (рис. 1). Так как движение точки равномерное, то модуль скорости постоянен. Например, за очень малое время точка переместилась из положения А1 в положение В1 (на рис. 2 для наглядности перемещение А1 В1 показано увеличенным).
|
|
Тогда по общему определению скорости линейная скорость на участке направлена вдоль хорды А1 В1. так как хорда при уменьшении промежутка времени все более приближается к дуге, то вектор скорости в середине участка А1 В1 (в точке С) направлен по касательной к дуге.
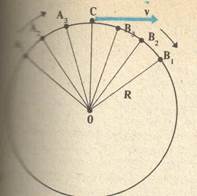
Рисунок 2.
Следовательно, и мгновенная скорость в любой другой точке окружности направлена по касательной. В этом можно убедиться, если прижать к вращательному точильному камню конец стального прутка. Раскаленные частицы, отрывающиеся от камня и летящие с той скоростью, которой они обладали в момент отрыва, будут видны в виде искр.
Направление вылета искр всегда совпадает с касательной к окружности в той точке, где пруток касается камня, по касательной окружности движутся и брызги от колес буксующего автомобиля (рис 3). Таким образом, линейная скорость тела, движущегося по окружности, оставаясь постоянной по модулю, непрерывно изменяется по направлению и в любой точке направлена по касательной к траектории.

Рисунок 3.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено - это есть период T. Путь, который преодолевает точка - это есть длина окружности.
Линейная скорость вычисляется по формуле:
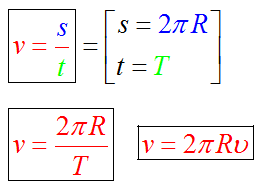
где
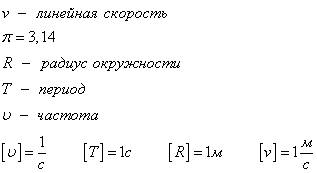
Угловая скорость.
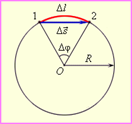
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
|
|
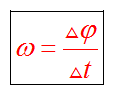
где
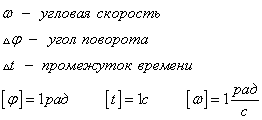
Период и частота.
Период вращения T - это время, за которое тело совершает один оборот.
Частота вращение - это количество оборотов за одну секунду.
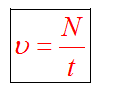
где
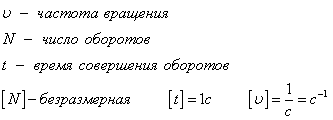
Частота и период взаимосвязаны соотношением
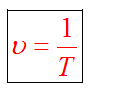
где

Связь с угловой скоростью
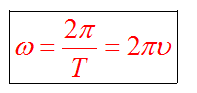
где