Лекция 7
Реляционная алгебра.
Основной набор операторов:
1) проекция
2) выборка
3) объединение
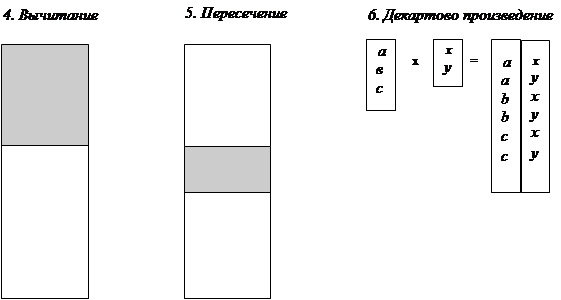
4) вычитание
5) пересечение
6) декартово произведение
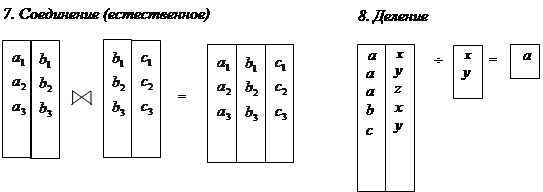
7) соединение (естественное)
8) деление
Первые пять из них можно рассматривать как примитивные, в том смысле, что ни один из них не выражается через другие. Это минимальный набор. Но на практике три остальные столь часто используются, особенно соединение, что имело смысл обеспечить их непосредственную поддержку, хотя они и не примитивны.
1. Основная цель алгебры - обеспечить запись выражений. Т.к. эти выражения символические и высокоуровневые, то ими можно манипулировать в соответствии с многочисленными правилами преобразования. В частности, реляционная алгебра служит хорошим базисом для оптимизации.
2. Фундаментальная природа реляционной алгебры позволяет оценить возможности определенного реляционного языка для выражения пользовательских намерений. Язык называют реляционно полным, если его возможности соответствуют основному набору реляционных операторов.
Качественная интерпретация реляционных операторов.
|
| ||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 |
Формальные определение операторов.
Проекция.
Пусть
 - исходное отношение,
- исходное отношение,
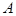 - подмножество его атрибутов,
- подмножество его атрибутов,
тогда
проекция - унарная операция 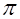 над отношением
над отношением  :
:

 ,
,
где
 - результирующее отношение,
- результирующее отношение,
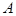 - его схема.
- его схема.
Следовательно, проекция возвращает отношение  с заданными атрибутами. При этом повторяющиеся кортежи в отношении
с заданными атрибутами. При этом повторяющиеся кортежи в отношении  должны быть исключены.
должны быть исключены.
Например: для отношения “Поставщик”


Выборка.
Пусть
 - исходное отношение,
- исходное отношение,
 - подмножество его атрибутов, причём
- подмножество его атрибутов, причём  - скаляр.
- скаляр.
Кроме того,
 и
и  - сравнимые атрибуты в
- сравнимые атрибуты в  (определены на одном домене), а
(определены на одном домене), а
 - множество бинарных операций.
- множество бинарных операций.
Тогда
выборка (ограничение) - это унарная операция s над отношением  по формуле
по формуле 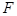 :
:
 ,
,
где
 - результирующее отношение,
- результирующее отношение,
 или
или  .
.
Следовательно, выборка возвращает отношение  , содержащее все те кортежи отношения
, содержащее все те кортежи отношения 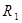 , которые удовлетворяют заданному условию
, которые удовлетворяют заданному условию 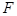 .
.
Например: для отношения “Деталь”

Объединение
Пусть
 и
и  - исходные отношения,
- исходные отношения,
 - их схемы (Þ степень
- их схемы (Þ степень  ),
),
 и
и  - их кардинальные числа.
- их кардинальные числа.
Тогда
объединение  - отношение, у которого:
- отношение, у которого:
схема  (Þ степень
(Þ степень  ),
),
кардинальное число  .
.
Следовательно, кортежи результирующего отношения принадлежат одному или обоим исходным отношениям. При этом повторяющиеся кортежи удаляются.
Вычитание
Допущения (см. операцию 3).
Тогда
вычитание 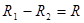 - отношение, у которого:
- отношение, у которого:
схема  (Þ степень
(Þ степень  ),
),
кардинальное число  .
.
Следовательно, кортежи результирующего отношения принадлежат уменьшаемому отношению и не принадлежат вычитаемому отношению (повторяющихся кортежей быть не может).
Пересечение
Допущения (см. операцию 3).
Тогда
пересечение 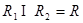 - отношение, у которого:
- отношение, у которого:
схема  (Þ степень
(Þ степень  ),
),
кардинальное  .
.
Следовательно, кортежи результирующего отношения принадлежат обоим исходным отношениям (повторяющихся кортежей быть не может).
Декартово произведение
Пусть
 и
и  - исходные отношения, не имеющие обоих атрибутов,
- исходные отношения, не имеющие обоих атрибутов,
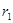 и
и  - схемы этих отношений,
- схемы этих отношений,
 и
и  - их кардинальные числа,
- их кардинальные числа,
 и
и 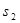 - их степени.
- их степени.
Тогда
декартово произведение  - отношение, у которого:
- отношение, у которого:
схема  (объединение схем),
(объединение схем),
кардинальное число  ,
,
а степень 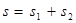 .
.
Следовательно, кортежи результирующего отношения образуются всевозможными парными сочетаниями кортежей исходных отношений.
Соединение (естественное)
Пусть
 и
и  - исходные отношения, имеющие подмножество А0 общих атрибутов (определенных на одном домене),
- исходные отношения, имеющие подмножество А0 общих атрибутов (определенных на одном домене),
 и
и  - множества значений
- множества значений  и
и 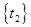 общих атрибутов в картежах исходных отношений,
общих атрибутов в картежах исходных отношений,
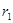 и
и  - схемы этих отношений,
- схемы этих отношений,
 и
и  - их кардинальные числа,
- их кардинальные числа,
 и
и 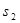 - их степени.
- их степени.
Тогда
соединение -  отношение, у которого:
отношение, у которого:
 , при этом
, при этом
схема  ,
,
кардинальное число  ,
,
а степень  .
.
Следовательно, кортежи результирующего отношения образуются всевозможными парными сочетаниями кортежей исходных отношений с равными значениями общих атрибутов.
Примечание: при отсутствии общих атрибутов соединение превращается в декартово произведение.
Q-соединение
Пусть
 и
и  - исходные отношения, которые не имеют общих атрибутов, но имеют сравнимые атрибуты
- исходные отношения, которые не имеют общих атрибутов, но имеют сравнимые атрибуты  и
и  ,
,
 и
и  - схемы этих отношений,
- схемы этих отношений,
 и
и  - их кардинальные числа,
- их кардинальные числа,
 и
и 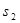 - их степени.
- их степени.
 - множество бинарных операций для сравнимых атрибутов.
- множество бинарных операций для сравнимых атрибутов.
Тогда
Q-соединение  - отношение, все кортежи которого удовлетворяют условию
- отношение, все кортежи которого удовлетворяют условию  , причем у результирующего отношения:
, причем у результирующего отношения:
схема  (объединение схем),
(объединение схем),
кардинальное число  ,
,
а степень 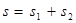 .
.
Деление
Пусть
 и
и  - исходные отношения, с множеством атрибутов,
- исходные отношения, с множеством атрибутов, 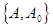 и
и  соответственно, так что
соответственно, так что  - общие атрибуты, определенные на одном домене,
- общие атрибуты, определенные на одном домене,
 и
и  - множества значений общих атрибутов в кортежах.
- множества значений общих атрибутов в кортежах.
Тогда
деление 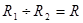 - отношение, со схемой
- отношение, со схемой  , все кортежи
, все кортежи  которого являются элементами множества
которого являются элементами множества 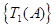 , сформулированного по условию
, сформулированного по условию  .
.
Например:
1. Получить имена поставщиков, которые поставляют деталь Д2:

2. Получить имена поставщиков, которые поставляют по крайней мере одну красную деталь:
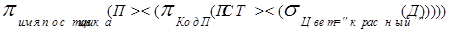
3. Получить номера поставщиков, поставляющих по крайней мере все те детали, которые поставляет поставщик П2:

4. Получить имена поставщиков, которые не поставляют деталь Д2:

