• Риск связан с стремлением проектировщиков использовать старый опыт в новых условиях проектирования, а
• неопределенность - с недостаточностью информации при проектировании о создаваемой системе.
4. Современное проектирование всегда связано с ограниченностью ресурсов, результаты проектирования должны быть получены в определенное время, ценой ограниченных средств (материальных, финансовых, и т.д.)
5. Использование современных ИТ при проектировании
12. Персональная ответственность и рациональное поведение – как принципы системного проектирования.
Анализ практики проектирования свидетельствует, что оптимальное расределение ресурсов при проектировании основывается на использовании следующих принципов:
Принцип рационального поведения определяет стремление человека к максимимизации качества проектируемой системы.
Исходя из этого принципа, проектирование характеризуется стремлением максимально использовать возможности человека, входящего в состав сложной ИС.
Для этого ему стремятся создать оптимальные условия для работы в составе БТС, рационально распределить функции между человеком и машинной частью системы.
Принцип персональной ответственности предопределяет наличие человека, наделенного полномочиями принимать решения в ходе проектировании БТС и нести персональную ответственность за результаты принятого решения.
Таким человеком является главный конструктор системы (руководитель темы, главный специалист проекта и т.п.) Он осуществляет руководство и координацию работ по созданию новой системы, а также наблюдает за производством и эксплуатацией Системы на всех этапах ее жизненного цикла.
13. Принцип системного подхода при проектировании.
Системный подход представляет собой методологию исследования, в основе которого лежит утверждение, что специфика системы, ее особенности определяются не просто особенностями составных частей и ее элементов, а опред прежде всего характером связи и отношениями, опред структуру систем.
При системном подходе:
1. Все средства БТС рассматриваются как некоторая opганизация, единое целое, входящая в систему высшего уровня иepархии, и предназначенная для решения определенной задачи. Качество БТС характеризуется единым объективным показателем качества.
2. Все средства БТС оцениваются с точки зрения их влияния на выбранный показатель качества.
3. При проектировании БТС обязательно учитываются экономические аспекты проблемы.
14. Математический аппарат и объекты формализации при системном проектировании ИИС.
При системном подходе проектировщик ИИС всегда стремится к максимизации качества системы, выраженного некоторым формальным показателем качества. При этом множество вариантов построения ИИС определяется эвристически, а оптимальный вариант выбирается путем сравнения рассматриваемых вариантов по показателю качества, выраженного количественной величиной.
Показатель качества ИИС может быть определен на основании анализа моделей ИИС, поэтому объектами формализации при системном подходе к проектированию являются:
- структура ИИС (внешняя и внутренняя), ее состав и связи;
- параметры, характеризующие ИИС, в качестве которых мы рассмотрим
q показатель качества ИИС и
q зависимость качества ИИС от ресурсов
Практика системного проектирования показывает, что для формализации указанных понятий используется аппарат теории множеств и аппарат теории функциональных пространств.
Достоинством этого аппарата является возможность описания поведения ИИС (ее функционирования) в условиях риска и неопределенности с помощью конкретных математических выражений, а
недостатком - невозможность адекватного описания поведения человека, входящего в качестве составного элемента в состав ИИС.
16.Понятие внешней и внутренней структуры БТС.
Под внутренней структурой понимают составные части системы и связи. При этом параметры отдельных составных частей системы называют внутренними параметрами. Под внешней структурой системы понимают саму систему и ее «окружение». Окружение – это другие системы или факторы, которые оказывают влияние на исследуемую систему в процессе ее функционирования. Окружение иногда называют внешней средой. Те параметры системы, которые проявляются впроцесса взаимодействия системы и внешней среды, называются внешними параметрами системы.
17.Использование операций относительного дополнения и симметрической разности при системном проектировании.
4. Относительное дополнение \.
Дополнение множества В до множества А.
Эта операция позволяет исключить из рассматриваемой системы элементы связи с другими подсистемами.
5. Симметрическая разность Å, ¸.
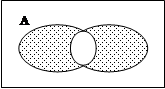Операция симметрицеской разности позволяет исключить из рассматриваемой системы, состоящей из нескольких взаимосвязанных подсистем, элементы связи этих подсистем (общие элементы).
1. Коммутативность А Å В = В Å А
2. Ассоциативность (А Å В) Å С = А Å (В Å С)
А Å А = Æ, А ÅÆ = А
15. Формализация состава ИИС: понятие элемента, подсистемы, системы. Отношения принадлежности и включения.
ИИС, отнесенная нами к классу больших технических систем,рассматривается как некоторая организация, единое целое, элементов (отдельные технические средства системы) и связей между ними
Элементы ИИС вместе с относящимися к ним связями могут разделены на группы (подсистемы) по функциональному признаку.
Внутренняя структура ИИС, как было показано ранее (при рассмотрении характеристических свойств БТС), имеет иерархический характер построения (ИИС->подсистемы->элементы)
Различные уровни иерархии (атакже компоненты одного уровня) объединены связями, которые входят в состав ИИС.
В такой постановке ИИС (ее состав) может быть представлен как некоторое конечное, абстрактное множество и обозначается заглавными буквами латинского алфавита: А,В,С,...
Подсистемы ИИС формализуются через теоретико-множественное понятие подмножества, которые мы будем обозначать заглавными - буквами латинского алфавита с нижними индексами: Al, A2,...,Ai,...Am i = 1.. m
Элементы ИИС (ее подсистем) при формальном подходе рассматриваются как элементы множества, являющегося моделью ИИС (или ее подсистем). Они обозначаются малыми прописными буквами латинского алфавита: а1,а2,...,аj,...,аn j = 1.. n
Таким образом состав ИИС, отображаемый некоторым множеством л. может быть представлен через:
1) полный перечень отображений всех входящих в ее состав элементов:
А={а1,а2,... аn }
2) полный перечень отображении всех входящих в ее состав подсистем:
А={ Al, A2,...Am }
3) характеристический признак (отображение характеристического свойства f(ai)), определяющий принадлежность элемента ai к множеству А, отображающему ИИС:
А = { ai /f(ai) } i = 1.. n
Формальным отображением связей ИИС, формирующих ееорганизацию, являются отношения. Отношения устанавливают факт существования связей между элементами, но не определяют их характера.
При формализации состава ИИС используются отношения принадлежности и включения.
Отношение принадлежности Î определяет входит или не входит рассматриваемый элемента в состав множества А:
Запись: а ÎА –входит, аÏА - не входит.
Отношение включения Í определяет входит или не входит рассматриваемая подсистема Аi в множество А, отображающее ИИС.
Запись: АiÍА – входит, АiË А - не входит, BÌAÞB¹A
Í - нестрогое включение
Ì - строгое включение
Отношения включения обладают тремя свойствами:
* рефлексивность: АÍА,
* транзитивность: А ÍВ ÚВÍ С => AÍ С,
* симметричность: А ÍВ ÚВÍА => Aº В.
Кроме понятия простого включения существует понятие строгого включения Ì. Запись ВÌА означает, что система В является частью системы А (т.е. системы В и А не совпадают В ¹ А).
18. ИИС испытаний ЛА – как БТС.
1. Система контрольно-измерительных станций
2. Система промежуточных центров приема информации
3. Координационно-вычислительный центр
4. Центр управления экспериментом и распределения информации
5. Локальные центры обработки и распределения информации
6. Локальные потребители информации
7. Техническая позиция
8. Системы предстартового контроля
9. Стартовая позиция
10. Испытываемый ЛА на стартовой позиции
11. Испытываемый ЛА в полете
12. Поисково-спасательный комплекс
13. Имитационная модель летного эксперимента
14. Служба единого времени
Основные назначения ИИС являются получение информации, ее обработка и доведение результатов обработки до потребителя.
20. Использование понятий «универсальное множество» и «пустое множество» при системном проектировании.
При проектировании всегда рассматривается ограниченное число объектов или факторов, т.е. рассмотрение ведется в некоторых границах. Говорят, что система рассматриваемых множеств ограничена и образует так называемое универсальное множество.
Если А Ç В =Æ - нет общих элементов - запись формально отображает тот факт, что у систем А и В нет общих элементов, т.е. эти системы не связаны между собой и должны рассматриваться как изолированные друг от друга – пустое множество.
19. Использование операций «объединение, пересечение, абсолютноедополнение».
1. Операция объединения È
Операция объединения множеств является моделью композиции системы из известных подсистем и формализует собой представления об полном составе технических средств системы.
С = А ÈВ = {c / cÎAÚcÎB}
1. Рефлексивность A = А ÈA
2. Симметричность А ÈB = BÈA
А ÈÆ = А
2. ОперацияпересеченияÇ
Операция пересечения множеств является моделью множества элементов связи, т.е. элементов, объединяющих отдельные подсистемы в систему.
С = А Ç В = {c / cÎAÙcÎB}
1. Рефлексивность A = А Ç A
2. Симметричность А Ç B = B Ç A
А Ç Æ =Æ
ÆÍ А Ç В Í А ÍА È В
Если А Ç В =Æ - нет общих элементов - запись формально отображает тот факт, что у систем А и В нет общих элементов, т.е. эти системы не связаны между собой и должны рассматриваться как изолированные друг от друга
m(А ÈВ) = m(A) + m(B) – m(А ÇВ)
m(А Ç В) = m(A) + m(B) - m(А ÈВ)
В тех случаях, когда в процессе проектирования необходимо формализовать средства, которые не входят в состав рассматриваемой системы, но влияние которых должно учитываться при анализе поведения системы используются теоретико – множественные понятия дополнения множества или множеств. Различают абсолютные и относительные дополнения.
3. Абсолютное дополнение``
Внешняя среда системы.
21. Теоретико-множественная модель внутренней структуры БТС.
Рассмотренные выше операции теории множествпозволяют сформировать теоретико-множественную модель состава любой системы.
Модель состава может быть преобразована в модель структуры путем наложения на нее системы отношений, характеризующих связи между элементами подсистем.
Модель структуры отражает организацию системы.
Модель внутренней структуры систем с явно выраженными связями может быть задана как прямое или декартовое произведение конечного количества множеств.
С = А´В ={<a, b> | aÎA, bÎB}
Модель в виде декартового произведения представляются множеством упорядоченных пар, определяющих отношения или связи между элементами рассматриваемых подсистем.
В случае, когда система состоит из нескольких подсистем, модель внутренней структуры имеет вид декартового произведения n множеств.
A = A1´A2´… ´An= {< a1, a2,…, an> | a1ÎA1, a2ÎA2, …, anÎ An}
22. Теоретико-множественная модель внешней структуры БТС.
Процесс эксплуатации ИИС рассматривается нами как процесс взаимодействия ИИС со средой (среда - это все то, что входит в окружение системы при данном ее рассмотрении).
Под теоретико-множ. Моделью внешней струкуры, будем понимать ввиде декартового произведения 2ух множеств, первое из кот Ai – явл моделью внутрстр-рысиситемы, а Aj – моделью во внешней среде.
Поскольку процесс взаимодействия ИИС со средой охватывает конечное число объектов, то в качестве модели взаимодействия может выступать прямое произведение множеств:
A = Ai ´ Aj ={< ai, aj > | ai Î Ai, aj Î Aj }
Здесь Ai и Aj являются формальными объектами, отображающими ИИС (AiAj) и среду (AiAj), которые связаны отношениями, характеризующими связи между ИИС и средой в процессе их взаимодействия.
Для более детального отображения взаимодействия ИИС со средой позволяющего учесть состав среды и ИИС, а также их внутреннюю структуруиспользуетсяпрямоепроизведениевида:
A = A1 ´ A2 ´ … ´ An ={ <a1, a2,…, an> | a1 Î A1, a2 Î A2 ,…, an Î An }
Здесь Ai - формальное отображение некоторого объекта или фактора, входящего в состав ИИС или среды и учитываемого при описании взаимодействия (ими могут быть: средства ИИС, входящие в ее состав, отдельные компоненты среды, включая и другие системы, человек и т.д., а также объединяющие их связи).
Введенная теоретико-множественная модель взаимодействия ИИС со средой несет информацию как о системе, так и о среде, позволяет определить их границы и показывает какие объекты и факторы будут учитываться при системном проектировании ИИС.
Недостатком модели является то, что она не отображает явно (непосредственно) связи, случайный характер взаимодействия и возможные его ситуации.
24. Качество, эффективность и критерий эффективности БТС.
Под качеством системы будем понимать показатель, выражаемый через ее внешние параметры и характеризующий степень соответствия системы своему назначению при нахождении системы в некотором состоянии q из пространства существования Ds.
Эффективность является математическим ожиданием качества.
Критерий эффективности – число, которое характеризует эффективность и является её численной оценкой.
25. Ситуации взаимодействия ИИС со средой: детерминированная, риска и неопределённости.
1. Детерминированная ситуация
| 2. Ситуация риска
Знаем все возможные исходы и их вероятности.
|
3. Ситуация неопределённости
Не знаем все исходы и/или все вероятности.
23. Топологическая модель БТС и её значение при проектировании.
Топологическая модель БТС с учетом ее назначения:|DEDsPsDj|
Состояние ИИС в некоторый момент времени - обобщенный внешний параметр q: q = { q (1), q (2),…, q (n)}, где q (i) – i-ый внешний параметр системы, численно характеризующий ее i-ое внешнее свойство. Графически состояние ИИС представляется точкой в системе координат внешних свойств ИИС Ws. Множество состояний, в которых может находиться ИИС в процессе взаимодействия со средой, условимся называть пространством состояний ИИС (или пространством существования ИИС) Ds: qÎDs; Ds = { q }
Пространство Ds может быть как непрерывным, так и дискретным.
Влияние среды на характер модели ИИС проявляетсяв том, что в силу случайного характера среды и состояние системы носит случайный характер, содержит в себе элемент неопределенности.В любой момент времени t = ti ИИС может находиться только в одном состоянии q i, В силуслучайного характера взаимодействия ИИС со средой эти состоянием может быть любое состояние q i ÎDs. Вероятностной мерой наличия той или иной реализации q, учитывающей ее статистический характер, м.б. некоторая неотрицательная счетно-аддитивная функция Ps, определеннаянамножестве Ds, такая что:
P s(Ds) = 1; P s(
) = 
где q i Çq j = Æдля любых i¹j, а Ps - вероятностная мера, определенная на Ds. Для случая, когда функция Ps непрерывна на Ds можно положить, что dPs = g(q)dq и 
где g (q)- функция плотности вероятности состояния q. Функция g (q) называется функцией внешних условий и характеризует воздействие среды на состояние ИИС. Ps характеризует случайный характер взаимодействия ИИС со средой.
Влияние человека на состояние ИИС определяется зависящем от него распределением ресурсов системы по пространству Ds. Формально это может быть отображено путем наложения на Ds некоторого функционального отношения j, определяющего состояние ИИС и непрерывного на Ds: j = j(q). Человек может реализовать распределение ресурсов через выбор внутренней структуры ИИС, поэтому функцию j называют функцией построения системы.Человек может реализовать конечное множество построений ИИС: Dj = {j}; jÎDj. Для Dj, рассматриваемого нами как отображение множества возможных внутренних структур системы, Ds является пространством определения, а само Dj является множеством j -образов пространства Ds.
Для отражения назначения системы введём понятие эффективности.Под качеством системы будем понимать показатель, выражаемый через ее внешние параметры и характеризующий степень соответствия системы своему назначению при нахождении системы в некотором состоянии q из пространства существования Ds. Поскольку эффективность является математическим ожиданием качества, она может рассматриваться как мера, определенная на пространстве Ds. При известном пространстве существования Ds и заданной функции внешней среды Ps эффективность может рассматриваться как величина, зависящая от распределения ресурсов системы, т.е. от функции построения системы Dj. При этом возможным построением системы ji из пространства Dj будут соответствовать свои значения эффективности Еi, тогда множеству возможных построений системы можно поставить в соответствие множество значений эффективности DЕ.
26. Макромодель эффективности ИИС и ее компоненты.
Эффективность БТС в функции поведения человека через интеграл Лебега-Стилтьеса:
, где 
– качество БТС, соответствующее её состоянию q при некоторой реализации стратегии человека 
. 
определяет в данном случае условия ограничения:
.Ps –вероятностная мера, характеризующая случайный характер взаимодействия БТС со средой. 
– функция построения БТС, характеризующая воздействие на БТС человека, входящего в её состав; является формальным отображением её внутренней структуры, рассматривается как плотность распределения ресурсов БТС по пространству существования .
Интеграл Лебега — Стилтьеса может быть определен на любомвероятностном пространстве, если 
конечно: 
, где 
.
Для случая одноразового использования (непрерывный характер взаимодействия со средой): 
, где 
– функция внешних условий, характеризующая воздействие внешней среды на состояние БТС; формально рассматривается как плотность вероятности состояние БТС.
Для случая многоразового использования (дискретный характер взаимодействия со средой): 
, здесь каждое 
соответствует i -й реализации использования и определяется в соответствии с выражением для одноразового использования.
27. Отношения порядка: определение, свойства. Упорядоченные множества.
Отношения порядка – определяют, какой член пары, входящей в состав рассматриваемой модели БТС, должен считаться по значимости первым, а какой – вторым. Могут служить заменой любого другого отношения, характер которого по тем или иным причинам невозможно установить с достаточной точностью. В соответствии с информационным уровнем, на котором находится системное проектирование, разработчик может установить либо относительную значимость только некоторых элементов (средств) БТС (отношения частичного (нестрогого) порядка), либо упорядочить (ранжировать) весь состав БТС (вполне упорядоченныеотношения (строгого порядка)).
Свойства: для строго порядка антирефлексивность(
, ассиметричность (
), транзитивность (
); для нестрогого порядка рефлексивность(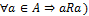
, антисимметричность (
), транзитивность ().
Если хотя бы для нескольких пар элементов a,b множества A можно по некоторому признаку установить, что 
или 
, то множество A называется частично упорядоченным и м.б. определено в своих границах (рассматриваемое множество конечно, и, следовательно, для реализации представляемой им БТС требуются конечные ресурсы). Вполне упорядоченные множества определяются тем, что для них отношение 
равносильно существованию цепи вида: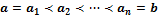 
, в которой между любыми элементами 
и 
не существует промежуточного элемента ( покрывает ). Вполне упорядоченное множество м.б. представлено в виде графа, в котором элементы множества изображаются вершинами графа в соотв. с правилом: вершина, изображающая элемент a, располагается выше вершины, изображающей элемент b в том и только в том случае, если , причём если a покрывает b, то они соединяются прямолинейным отрезком.
28. Отношения эквивалентности и тождественности: определения, свойства, значение при проектировании.
Эквивалентность – неразличимость элементов БТС по одному признаку (признаку эквивалентности). Свойства: рефлексивность (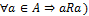, симметричность (
, транзитивность (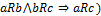
. Отношение эквивалентности может рассматриваться как формализация признаков, используемых для функционального разделения БТС на подсистемы в ходе системного проектирования (декомпозиция БТС). В подсистемы объединяются элементы, эквивалентные по своему назначению.
Частным случаем деления (декомпозиции) БТС является выделение резерва для повышения надёжности БТС. Такая операция м.б. формализована путём использования представления об отношении тождества: 
. Оно означает, что резервный элемент b, связанный с некоторым 
отношением тождества 
, отвечает условию 
. Свойства те же, что и у эквивалентности, плюс антисимметричность ().
29. Функциональные отношения. Композиция функций.
Функция в теории множеств рассматривается как отношение, характеристическим свойством которого является единственность ее образа в области определения. Это означает, что элементами функции являются упорядоченные пары: 
, обладающие тем свойством, что если 
. Функция, получающаяся из 
переменой мест элементов, называется функцией, обратной к , и обозначается 
. Для того, чтобы м.б. отличить, относится ли данная функция ко всей модели БТС или только к её части, вводится понятие о «функции, определённой на А »: 
, и «функции, определённой в А »: 
.
Композиция двух функций возможна только тогда, когда обе функции зависят от одного множества: 
, где 
- знак композиции.В данном случае и 
зависят от множества 
, для которого справедливо 
. Композиция ассоциативна, но в большинстве случаев не коммутативна: 
, но 
. Физически же ассоциативность композиции функциональных отношений означает, что общее представление о характере функциональных связей не зависит от объединения их в группы при условии, что при этом не нарушаются предпочтения, определённые на частных функциональных связях. В противном случае представление о характере связей может существенно измениться.
30. Эффективностьи критерий эффективности как формы оценоккачества ИИС. Свойства эффективности.
Под качеством системы будем понимать показатель, выражаемый через ее внешние параметры и характеризующий степень соответствия системы своему назначению при нахождении системы в некотором состоянии q из пространства существования Ds.
Поскольку эффективность является математическим ожиданием качества, она может рассматриваться как мера, определенная на пространстве Ds со следующими свойствами:
1. " Ds: 0 <E<µ
При известном пространстве существования Ds и заданной функции внешней среды Ps эффективность может рассматриваться как величина, зависящая от распределения ресурсов системы, т.е. от функции построения системы Dj. При этом возможным построением системы ji из пространства Dj будут соответствовать свои значения эффективности Еi, тогда множеству возможных построений системы можно поставить в соответствие множество значений эффективности DЕ.
Dj = {ji }Û DE = { Еi }
2. DsiÌ DsÛEiÎ DE.
Любому подпространству Dsi пространства существования соответствует свое значение эффективности Ei либо значение эффективности DE.
3. Ds = 
Dsi, " i¹j: DsiÇDsj= ÆÞ E = S Ei
Эффективность аддитивна
e: Е Û R’
Число e, которое характеризует эффективность и является ее численной оценкой, будем называть критерием эффективности.
DE Û D e
33. Экспертное ранжирование объектов (метод Штенгауза).
Если К-1 объект уже упорядочены и нужно найти место для К-то объекта, то этот К-ый объект сначала сравнивается с медианным (серединным) объектом уже имеющегося упорядочения. Если К-ый объект окажется более предпочтительным, чем медианный, то в дальнейшем он будет сравниваться с объектами верхней половины имеющегося конечного списка, иначе – с объектами нижней половины. При этом примерно половина проранжированных объектов из рассмотрения исключается. Процедура повторяется для оставшейся части списка до тех пор, пока место для объекта не будет найдено. На каждом шаге исключается примерно половина оставшейся части списка.
При нечетномК имеется два медианных элемента в рассматриваемом конечном списке и эксперт вправе выбрать любой из них. Число парных сравнений, необходимых для ранжирования Nэлементов, зависит не только от структуры исходного списка, но и от того, какие медианные элементы выбирает эксперт. Минимальное число сравнений 
при N>2, максимальное 
, где запись [a] означает целая часть числа a.
34. Экспертное ранжирование объектов (метод Штенгауза-Форда-Джонсона).
На первом этапе все ранжируемые объекты разбиваются на пары, в каждой из которых определяется более предпочтительный элемент. Если число ранжируемых элементов нечетно (N=2r+1), то один из элементов не участвует в этих парных сравнениях и в дальнейшем рассматривается вместе с менее предпочтительными элементами.
На втором этапе определенные r более предпочтительных элементов размещаются в порядке их предпочтительности с помощью алгоритма Штенгауза.
На третьем этапе - r (или r+1, если N - нечетно) менее предпочтительных элементов размешаются среди r более предпочтительных элементов, полученных на первом этапе и упорядоченных на втором этапе.