Условия: Определить суммарную абсолютную и относительную погрешности косвенного измерения, если известны расчетная формула, значения величин, входящих в формулу, и систематические погрешности прямых измерений этих величин. Данные, необходимые для расчета, приведены в табл. 14.1 и табл. 14.2.
Указания к решению
Из математического анализа известно, что если величина является функцией нескольких переменных
Y = f(x1, x2, …),
то абсолютная погрешность величины «у» определяется по формуле

где Dx1, Dx2 - абсолютные погрешности прямых измерений;
 - значения частных производных от функции по соответствующему
- значения частных производных от функции по соответствующему
аргументу.
После нахождения абсолютной погрешности косвенного измерения можно вычислить относительную погрешность косвенного измерения по формуле 
где у - искомая величина, определяемая по расчетной формуле.
Вопросы для самоконтроля
1. Что такое погрешность измерений и ее виды?
2. Систематические и случайные погрешности.
3. Предельные погрешности и их определение.
4. В чем заключаетсяопределение систематической погрешностей косвенных измерений?
5. В чем заключаетсяопределение случайной погрешности косвенных измерений?
Таблица 14.1
| Вариант | Расчетная формула | U, B | I, A | R, Ом | P, Вт | Q, кг/с | r, кг/м3 | V, м/с | S, м2 | DU, В | DI, А | DR, Ом | DP, Вт | DQ, кг/с | Dr, кг/м3 | DV, м/с | D S, м2 |
| Q=r×V×S | 1,5 | 12×10-4 | +10 | +0,05 | +0,2×10-4 | ||||||||||||
| R=U/I | +5 | +0,01 | |||||||||||||||
| V=Q/r×S | 1,2 | 12×10-4 | +0,02 | -10 | -0,1×10-4 | ||||||||||||
| P=U×I | +5 | -0,01 | |||||||||||||||
| r=Q/V×S | 1,2 | 10×10-4 | +0,02 | -0,04 | +0,2×10-4 | ||||||||||||
| U=P/I | 1,2 | -0,02 | +20 | ||||||||||||||
| S=Q/V×r | 0,8 | 1,2 | +0,02 | -12 | -0,04 | ||||||||||||
| I=U/R | -3 | +10 | |||||||||||||||
 9 9
| I=P/U | +5 | -20 | ||||||||||||||
| U=I×R | 4,5 | -0,1 | -1,8 | ||||||||||||||
| Q=r×V×S | 2,5 | 8×10-4 | -15 | +0,05 | +0,2×10-4 | ||||||||||||
| r=Q/V×S | 0,8 | 16×10-4 | +0,01 | +0,02 | -0,1×10-4 | ||||||||||||
| U=I×R | +0,08 | -1,2 | |||||||||||||||
| I=P/U | +2 | +15 | |||||||||||||||
| S=Q/V×r | 1,5 | 1,0 | +0,02 | +15 | +0,04 | ||||||||||||
| R=U/I | -5 | -0,1 | |||||||||||||||
| U=P/I | -0,05 | +12 | |||||||||||||||
| V=Q/r×S | 0,85 | 10×10-4 | +0,01 | +12 | -0,2×10-4 | ||||||||||||
| I=U/R | +3 | -10 | |||||||||||||||
| P=U×I | 6,5 | -2 | +0,02 |
Примечание. В формулах приняты обозначения: U - напряжение; I - ток; R - сопротивление; P - мощность;
Q - расход топлива; r - плотность топлива; V - скорость потока топлива; S - площадь сечения трубопровода.
 |
Таблица 14.2
| Вариант | Расчетная формула | Q, мм3 | l, мм | S, мм | h, мм | d, мм | E, кг×м2 с2 (Дж) | m, кг | V, м/с | DQ, мм3 | D l, мм | DS, мм | Dh, мм | Dd, мм | DE, кг×м2 с2 (Дж) | Dm, кг | DV, м/с |
| Q= l ×S×h | +0,05 | +0/05 | +0,05 | ||||||||||||||
| l =Q/S×h | -0,4 | -0,04 | -0,04 | ||||||||||||||
| S=Q/ l ×h | +4,5 | +0,1 | +0,1 | ||||||||||||||
| h=Q/ l ×S | -2,4 | -0,02 | -0,02 | ||||||||||||||
| Q= p×d 2×h | 2,5 | -0,05 | +0,01 | ||||||||||||||
 26 26
| 
| +0,5 | -0,01 | ||||||||||||||
| h=4Q/p×d2 | +1,0 | -0,04 | |||||||||||||||
| E=0,5m×V2 | +0,3 | -0,01 | |||||||||||||||
| m=2E/V2 | -2 | +0,01 | |||||||||||||||

| +3 | +0,04 |
Примечание. Вформулах приняты обозначения: Q - объем; l - длина; S - ширина; h - высота; d - диаметр;
E - кинетическая энергия; V - скорость; m - масса.
 |
Задача 15
Статистическая обработка результатов измерений
Условия: Выполнить статистическую обработку результатов измерений, приведенных в табл. 15.1.
При статистической обработке следует использовать результаты наблюдений при многократных измерениях для вариантов:
1, 2, 3, 4, 5 - сопротивления резистора Ri одинарным мостом;
6, 7, 8, 9, 10 - напряжения Ui компенсатором;
11, 12, 13, 14, 15 – диаметра di микрометром;
16, 17, 18, 19, 20 – массы mi электронными весами;
21, 22, 23, 24, 25 – тока Ii амперметром;
26, 27, 28, 29, 30 – давления Pi манометром.
Таблица 15.1
| Число наблюдений ni | Ri, Ом | Ui, В | di, мм | mi, г | Ii, А | Pi, Па |
| 9,791 | 9,91 | 33,71 | 650,64 | 10,26 | 40,92 | |
| 9,795 | 9,95 | 33,76 | 650,65 | 10,25 | 40,94 | |
| 9,789 | 9,89 | 33,72 | 650,62 | 10,23 | 40,91 | |
| 9,784 | 9,94 | 33,74 | 650,68 | 10,15 | 40,98 | |
| 9,796 | 9,96 | 33,73 | 650,98 | 10,24 | 40,96 | |
| 10,025 | 9,93 | 33,79 | 650,61 | 10,28 | 40,37 | |
| 9,793 | 9,94 | 33,80 | 650,68 | 10,96 | 40,97 | |
| 9,793 | 9,99 | 33,65 | 650,67 | 10,38 | 40,93 | |
| 9,765 | 9,95 | 33,82 | 650,63 | 10,32 | 40,95 | |
| 9,794 | 9,79 | 33,81 | 650,66 | 10,19 | 40,92 | |
| 9,797 | 9,97 | 33,32 | 650,62 | 10,22 | 40,99 | |
| 9,761 | 9,92 | 33,75 | 650,69 | 10,15 | 40,96 |
Таблица 15.2
| Вариант | Р | Вариант | Р | Вариант | Р |
| 0,90 | 0,95 | 0,99 | |||
| 0,95 | 0,98 | 0,998 | |||
| 0,98 | 0,95 | 0,98 | |||
| 0,99 | 0,90 | 0,95 | |||
| 0,998 | 0,999 | 0,90 | |||
| 0,999 | 0,90 | 0,999 | |||
| 0,90 | 0,95 | 0,95 | |||
| 0,95 | 0,98 | 0,90 | |||
| 0,95 | 0,998 | 0,95 | |||
| 0,98 | 0,99 | 0,98 |
Значения доверительной вероятности Р выбирается из табл. 15.2. в соответствии с вариантом задачи. Результаты расчета сводятся в табл. 15.3.
Таблица 15.3
| Номер наб-людения | Результаты наблюдений | Отклонение от среднего 
| 
| |||
| первичные | после исключения грубых погрешностей | по первичным наблюдениям | после исключения грубых погрешностей | по первичным наблюдениям | после исключения грубых погрешностей | |
| . . n | ||||||
| n = | 
| 
| 
| 
| 
| 
|
Пример. 1. Значения результатов наблюдения упорядочивают по возрастающим значениям в вариационный ряд х1, х2 ,..., xn.
Вариационный ряд результатов наблюдений при измерении сопротивления R (число наблюдений n = 10):
9,992; 9,995; 9,997; 9,999; 10,000; 10,001; 10,003; 10,005; 10,007; 10,121 Ом.
2. Определяется среднее арифметическое значение результатов наблюдений как
 .
.
3. Вычисляется оценка среднего квадратичного отклонения результатов наблюдений, то есть

4. Если значения хi резко отличаются от других членов вариационного ряда (промах, грубая погрешность), то их отбрасывают и в обработке результатов наблюдений не учитывают. Для проверки вида погрешности (грубая или значительная случайная) используется статистический критерий обнаружения грубых погрешностей (ГОСТ 11.002-73).
Суть статистического способа оценки результатов наблюдений заключается в том, что грубыми признают те погрешности, вероятность появления которых не превышает некоторого, заранее выбранного критерия.
Воспользуемся отбраковкой некоторых результатов измерений по критерию превышения отклонения среднего удвоенного значения среднего квадратичного отклонения результатов наблюдений  .
.
В случае обнаружения грубых погрешностей результаты наблюдений, их содержащие, исключаются, и математическая обработка повторяется. Для данного ряда проверим значение R10 = 10,121 Ом.
DRi = 10,121 -10,012=0,109 Ом; DRi = 0,109>2×0,04.
Отбрасываем R10, принимаем n = 9 и повторяем пп.2 и 3:
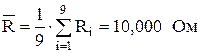 ;
;  .
.
5. Определяется доверительный интервал (границы) случайной погрешностирезультатов наблюдений как
Е = t×S,
где t - коэффициент (квантиль нормального распределения) Стьюдента, который в зависимости от вероятности Р и числа результатов наблюдений берется из табл. 15.4.
Таблица 15.4
Коэффициенты Стьюдента
| Число наблюдений n | Значение коэффициента Стьюдента t при при доверительной вероятности Р | |||||
| 0,9 | 0.95 | 0,98 | 0,99 | 0,998 | 0,999 | |
| 6,31 | 12,7 | 31,8 | 63,7 | 318,3 | 637,0 | |
| 2,92 | 4,30 | 6,96 | 9,92 | 22,33 | 31,6 | |
| 2,35 | 3,18 | 4,45 | 5,84 | 10,22 | 12,9 | |
| 2,13 | 2,78 | 3,75 | 4,60 | 7,17 | 8,61 | |
| 2,02 | 2,57 | 3,36 | 4,03 | 5,89 | 6,86 | |
| 1,94 | 2,45 | 3,14 | 3,71 | 5,21 | 5,96 | |
| 1,89 | 2,36 | 3.00 | 3,50 | 4,79 | 5,41 | |
| 1,86 | 2,31 | 2,90 | 3,36 | 4,50 | 5,04 | |
| 1,83 | 2,26 | 2,82 | 3,25 | 4,30 | 4,78 | |
| 1,81 | 2,23 | 2,76 | 3,17 | 4,14 | 4,59 | |
| 1,80 | 2,20 | 2,72 | 3,11 | 4,03 | 4,44 | |
| 1,78 | 2,18 | 2,68 | 3,05 | 3,93 | 4,32 | |
| 1,77 | 2,16 | 2,65 | 3,01 | 3,85 | 4,22 | |
| 1,76 | 2,14 | 2,62 | 2,98 | 3,79 | 4,14 | |
| 1,75 | 2,13 | 2,60 | 2,95 | 3,73 | 4,07 |
6. При нормальном законе распределения результатов наблюдений (при числе наблюдений n £15 принадлежность их нормальному закону не проверяют) математическое ожидание случайной величины М(х) с заданной вероятностью должно находиться в границах (доверительном интервале)
 ,
,
где  - среднее квадратичное отклонение действительного значения (среднего арифметического) результатов наблюдений,
- среднее квадратичное отклонение действительного значения (среднего арифметического) результатов наблюдений,
 , или
, или 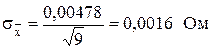 .
.
Коэффициент Стьюдента по табл. 14.4 для n-1=8 и Р=0,95; t=2,31.
Следовательно, доверительный интервал
10 - 2,31×0,0016 <R< 10+2,31×0,0016; или 9,996 < R <10,004.
Таким образом, при Р=0,95 доверительный интервал R = (10±0,004) Ом.
Вопросы для самоконтроля
1. Что такое выборочный контроль?
2. Что такое сплошной контроль и в каких случаях он применяется?
3. Как дать заключение о годности партии деталей при выборочном контроле?