Дифракция Френеля на круглом отверстии и диске. Восьмом.

10. Дифракция Фраунгофера на одной и на многих щелях. случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Расстояние должно быть таким, чтобы можно было пренебречь в выражении для разности фаз членами порядка, что сильно упрощает теоретическое рассмотрение явления. Иными словами, дифракция Фраунгофера наблюдается тогда, когда число зон Френеля, при этом приходящие в точку волны являются практически плоскими. Дифракционные явления Фраунгофера имеют большое практическое значение, лежат в основе принципа действия многих спектральных приборов, в частности, дифракционных решёток.
На одной щели: Дифракция Фраунгофера, имеющая большое практическое значение, наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию. Чтобы этот тип дифракции осуществить, достаточно точечный источник света поместить в фокусе собирающей линзы, а дифракционную картину исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием.

11. На дифракционной решетке: Большое практическое значение имеет дифракция, наблюдаемая при прохождении света через одномерную дифракционную решетку – систему паралл. щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками. Сравнивая с дифракцией Фраунгофера на щели, мы видим, что распределение интенсивности на экране определяется направлением дифрагированных лучей. Это означает, что перемещение щели параллельно самой себе влево или вправо не изменит дифракционной картины. Следовательно, если перейти от одной щели ко многим (к дифракционной решетке), то дифракционные картины, создаваемые каждой щелью в отдельности, будут одинаковыми.

12. Поляризация света. В естественном свете колебания направлений быстро и беспорядочно сменяют друг друга. Свет, в котором направления колебаний упорядочены каким-либо образом, называется поляризованным. Если колебания светового вектора происходят только в одной плоскости, свет называют плоско - (или линейно -) поляризованным.

13. Естественный и поляризованный свет.
в двенадцатом.

14. Закон Малюса. Пусть на поляризатор падает линейно-поляризованный свет амплитуды A₀ и интенсивности I₀. Сквозь прибор пройдет составляющая колебания с амплитудой A = A₀ cos?, где? – угол между плоскостью колебаний падающего света и плоскостью поляризатора. Следовательно, интенсивность прошедшего света I определяется выражением:
I = I₀ cos ²?. (1)

15. Закон Брюстера. закон оптики, выражающий связь показателей преломления двух диэлектриков с таким углом падения света, при котором свет, отражённый от границы раздела диэлектриков, будет полностью поляризованным в плоскости, перпендикулярной плоскости падения. При этом преломлённый луч частично поляризуется в плоскости падения, и его поляризация достигает наибольшего значения (но не 100%, поскольку от границы отразится лишь часть света, поляризованного перпендикулярно к плоскости падения, а оставшаяся часть войдёт в состав преломлённого луча). Угол падения, при котором отражённый луч полностью поляризован, называется углом Брюстера ^[1]. При падении под углом Брюстера отражённый и преломлённый лучи взаимно перпендикулярны.Это явление оптики названо по имени шотландского физика Дэвида Брюстера, открывшего его в 1815 году.

16. Двойное лучепреломление. В 1875 г. Керр обнаружил, что в жидкостях (и в аморфных твердых телах) под действием электрического поля возникает двойное лучепреломление. Это явление получило название эффекта Керра. Эффект Керра объясняется оптической анизотропией молекул жидкости, т. е. различной поляризуемостью молекул по разным направлениям. В результате жидкость становиться анизотропной. Ориентирующему действию поля противиться тепловое движение молекул. Этим обусловливается наблюдающееся на опыте уменьшение постоянной Керра В с повышением температуры.

17. Дисперсия света. Один из самых наглядных примеров дисперсии — разложение белого света при прохождении его через призму (опыт Ньютона). Сущностью явления дисперсии является различие скоростей распространения лучей света c различной длиной волны в прозрачном веществе —оптической среде (тогда как в вакууме скорость света всегда одинакова, независимо от длины волны и следовательно цвета).

18. Итак, дисперсия света – это зависимость показателя преломления вещества от частоты световой волны. Эта зависимость не линейная и не монотонная. Области значения ν, в которых соответствуют нормальной дисперсии света (с ростом частоты ν показатель преломления n увеличивается). Нормальная дисперсия наблюдается у веществ, прозрачных для света. Например, обычное стекло прозрачно для видимого света, и в этой области частот наблюдается нормальная дисперсия света в стекле. На основе явления нормальной дисперсии основано «разложение» света стеклянной призмой монохроматоров. Дисперсия называется аномальной, если т.е. с ростом частоты ν показатель преломления n уменьшается. Аномальная дисперсия наблюдается в областях частот, соответствующих полосам интенсивного поглощения света в данной среде. Например, у обычного стекла в инфракрасной и ультрафиолетовой частях спектра наблюдается аномальная дисперсия.

19. Тепловое излучение: Тела, нагретые до достаточно высоких температур, светятся. Свечение тел, обусловленное нагреванием, называется тепловым (температурным) излучением. Тепловое излучение, являясь самым распространенным в природе, совершается за счет энергии теплового движения атомов и молекул вещества.

20. Абсолютное черное тело: Тело, способное поглощать полностью при любой температуре все падающее на него излучение любой частоты, называется черным. Спектральная поглощательная способность черного тела для всех частот и температур тождественно равна единице (А_v,T = 1). Идеальной моделью черного тела является замкнутая полость с небольшим отверстием О, внутренняя поверхность которой зачернена

21. Закон Кирхгофа: Кирхгофустановил количественную связь между спектральной плотностью энергетической светимости и спектральной поглощательной способностью тел. Отношение спектральной плотности энергетической светимости к спектральной поглощательной способности не зависит от природы тела; оно является для всех тел универсальной функцией частоты (длины волны) и температуры (закон Кирхгофа): .

22. Законы излучения абсолютного черного тела:закон Стефана-Больцмана, законы Вина: Спектральная плотность энергетической светимости черного тела является универсальной функцией, поэтому нахождение ее явной зависимости от частоты и температуры является важной задачей теории теплового излучения. Закон Стефана-Больцмана: (на счет степени не уверен). - постоянная Стеф.- Больц.

Закон(смещения)Вина: опираясь на законы термо- и электродинамики, Вин установил зависимость длины волны l_max, соответствующей максимуму функции r_l,T от температуры Т: , т. е. длина волны l_max, соответствующая максимальному значению спектральной плотности энергетической светимости r_l,Tчерного тела, обратно пропорциональна его термодинамической температуре, b - постоянная Вина; ее экспериментальное значение равно 2,9×10^{-3 м}×К.

Закон(излучения) Вина: r_v1,T = Cv³Ae^-Av/T, гдеr_v1,T - спектральная плотность энергетической светимости черного тела, С и А - постоянные величины.

23. Противоречие классической физики: в рамках классической физики не удалось объяснить законы распределения энергии в спектре черного тела, так как формула Рэлея - Джинса резко расходится с экспериментом (проводимым при малых частотах и больших температурах), а также с законом смещения Вина, и оказалось, что попытка получить закон Стефана - Больцмана из формулы Рэлея - Джинса приводит к абсурду. Этотрезультат получил название «ультрафиолетовой катастрофы».

24. Квантовая гипотеза и формула Планка: Квантовая гипотеза - атомные осцилляторы излучают энергию не непрерывно, а определенными порциями - квантами, причем энергия кванта пропорциональна частоте колебания:

. где h= 6,625×10^-34 Дж×с - постоянная Планка.
Формула Планка: .

25. Внешний фотоэффект и его законы: Внешним фотоэлектрическим эффектом (фотоэффектом) называется испускание электронов веществом под действием электромагнитного излучения. Внешний фотоэффект наблюдается в твердых телах, а также в газах на отдельных атомах и молекулах.

I.При фиксированной частоте падающего света число фотоэлектронов, вырываемых из катода в единицу времени, пропорционально интенсивности света (сила фототока насыщения пропорциональна энергетической освещенности Е_екатода).

II.Максимальная начальная скорость (максимальная начальная кинетическая энергия) фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой v.

III.Для каждого вещества существует красная граница фотоэффекта, т. е. минимальная частота v₀ света (зависящая от химической природы вещества и состояния его поверхности), ниже которой фотоэффект невозможен.

26. Энергия и импульс световых квантов: При распространении в пространстве свет ведет себя подобно совокупности каких-то частиц, такие частицы получили название квантов света, или фотонов. Если фотон обладает энергией, то он должен обладать и импульсом.Связь между давлением и импульсом при движении частицы в теории относительности выражается формулой: при (для фатона)

27. Формула Эйнштейна для внешнего фотоэффекта.

Эйнштейн предположил, что фотон может выбить с поверхности только один электрон, а электрону, чтобы вырваться из вещества, необходимо совершить работу выхода А _вых. Тогда из закона сохранения энергии следовало, что при фотоэффекте энергия фотона h n должна быть равна сумме работы выхода А _вых и кинетической энергии фотоэлектрона со скоростью v и массой m:

Уравнение (30.3), объясняющее все законы фотоэффекта, называют уравнением Эйнштейна для фотоэффекта. Чем больше фотонов, тем больше они выбивают фотоэлектронов. Это и является объяснением закона №1 фотоэффекта. Согласно (30.3) кинетическая энергия фотоэлектронов прямо пропорциональная частоте света и не зависит от его интенсивности, что и объясняет закон №2 фотоэффекта. Из уравнения (30.3) следует, что фотоэлектрону необходимо совершить работу выхода А _вых, и свет с частотой меньше n_мин = А _вых/ h не будет вызывать фотоэффекта, что и объясняет закон №3 фотоэффекта.

28. Давление света.

Если фотон обладает импульсом, то свет, падающий на тело, должен оказывать на него давление. С точки зрения квантовой теории, давление света на пов-ть обусловлено тем, что каждый фотон при соударении с пов-тью передает ей свой импульс. Рассчитаем с точки зрения квантовой теории световое давление, оказываемое на пов-ть тела потоком монохроматического излучения (частота ), падающего перпендикулярно пов-ти. Если в единицу времени на единицу площади пов-ти тела падает N фотонов, то при коэффициенте отражения света от пов-ти тела отразится фотонов, а -- поглотится. Каждый поглощенный фотон передает пов-ти импульс , а каждый отраженный -- (при отражении импульс фотона изменяется на ). Давление света на пов-ть равно импульсу, который передают пов-ти в 1 с N фотонов:

29. Опыты Лебедева.

Схема опыта Лебедева по измерению давления света на твердые тела изображена на рисунке - 4.65. Свет, исходящий от источника S, пройдя через систему линз, попадает на поверхность зеркала З1. Отраженный от З₁ свет с помощью зеркал З₃ и 3₄ направляется на поверхность крыльев, которые находятся внутри баллона. Крылья, расположенные симметрично относительно оси подвеса, являются составной частью чувствительных крутильных весов, с помощью которых определяется сила давления света. Под действием света малоинертные подвески поворачиваются на определенный угол вокруг нити подвеса. Зная модуль кручения нити, можно определить силу действия света на подвески, а следовательно и давление света.

Результаты эксперимента позволили сделать следующие выводы:

1) давление света на зеркальную поверхность в два раза больше, чем давление на поверхность, полностью поглощающую свет;

2) величина давления света с точностью до 20% соответствует значению, полученному теоретически Максвеллом.

Классические опыты П. Н. Лебедева по измерению давления света явились фундаментальным доказательством и волновой, и квантовой природы света. Рассчитаем с точки зрения квантовой теории световое давление, оказываемое на поверхность тела потоком монохроматического излучения (частота ν), падающего перпендикулярно поверхности. Если в единицу времени на единицу площади поверхности тела падает N фотонов, то при коэффициенте отражения ρ света от поверхности тела ρN фотонов отразится, а (1—ρ)N — поглотится. Каждый поглощенный фотон передает поверхности импульс p_ν = hν/c, а каждый отраженный — 2p_v = 2hν/c (при отражении импульс фотона изменяется на —рν). Давление света на поверхность равно импульсу, который передают поверхности в 1 секунду N фотонов:

Nhv = E_e - есть энергия всех фотонов, падающих на единицу поверхности в единицу времени, т. е. энергетическая освещенность поверхности, а E_e/c = w — объемная плотность энергии излучения. Поэтому давление, производимое светом при нормальном падении на поверхность, равно

Эта формула, выведенная на основе квантовых представлений, совпадает и с экспериментальными данными, и с теоретическими данными, рассчитанными другими методами.

30. Квантовое объяснение давлениясвета.

32. Эффект Комптона.
некогерентное рассеяние фотонов на свободных электронах. Эффект сопровождается изменением частоты фотонов, часть энергии которых после рассеяния передается электронам. Обнаружен американским физикомАртуром Комптоном в 1923 году в экспериментах с рентгеновским излучением.
При рассеянии фотона на покоящемся электроне частоты фотона и (до и после рассеяния соответственно) связаны соотношением: где — угол рассеяния (угол между направлениями распространения фотона до и после рассеяния).

Перейдя к длинам волн:

где — комптоновская длина волны электрона, равная м.
Уменьшение энергии фотона в результате комптоновского рассеяния называется комптоновским сдвигом. Объяснение эффекта Комптона в рамках классической электродинамики невозможно, так как рассеяние электромагнитной волны на заряде (томсоновское рассеяние) не меняет её частоты.
Эффект Комптона является одним из доказательств справедливости корпускулярно-волнового дуализма микрочастиц и подтверждает существование фотонов.
Закон сохранения энергии в случае эффекта Комптона можно записать следующим образом^[1]:

где — релятивистская масса электрона, выражаемая через его скорость следующей формулой:

33. Принцип устройства лазера.

Лазер — оптический квантовый генератор, устройство, генерирующее когерентные электромагнитные волны за счёт вынужденного испускания или вынужденного рассеяния света активной средой, находящейся в оптическом резонаторе.
Лазер содержит три основных компонента: активную среду (активный элемент), в которой создают инверсию населённостей; устройство для создания инвер­сии в активной среде (система накач­ки); устройство для обеспечения поло­жит, обратной связи (оптический резона­тор). Простейший оптический резонатор (резонатор Фабри — Перо) состоит из двух плоских зеркал, расположенных параллельно, В оптическом резонаторе мо­жет существовать множество собственных стоячих волн, отличающихся тем, что для каждой из них между зеркалами укладывается целое число полуволн.

34. Трех- и четырехуровневые схемы работы лазеров.

35. Линейчатые спектры атомов: Спектры атомов - оптические спектры, получающиеся при испускании или поглощении электромагнитного излучения свободными атомами. Линейчатые - то есть состоят из отдельных спектральных линий, характеризуемых частотой излучения v, которая соответствует квантовому переходу между уровнями энергии E_i и E_kатома согласно соотношению: hv = E_i-E_k где h-постоянная Планка. Вид спектра зависит как от электронного строения данного атома, так и от внешних условий - температуры, давления, напряженностей электрического и магнитного полей и т. п.

36. Правило частот Бора: 2-ой постулат Бора(правило частот): При переходе атома из одного стационарного состояния в другое излучается или поглощается 1 фотон.

hv_kn = E_k-E_n, где k и n - номера стационарных состоянии; v_kn – частота фотона; h – постоянная Планка

При Ек<Еn происходит поглощение фотона, Ек>Еn – излучение.

37. Стационарное уравнение Шредингера для атомов водорода:

, где – волновая функция; x,y,z – координаты электронов; m – масса покоя электрона; E – полная энергия электрона; U – потенциальная энергия, которой обладает электрон в атоме водорода.

38. Водородоподобные атомы: Водородоподобные атомы - атомы (ионы), состоящие, подобно атому водорода, из ядра и одного электрона. К ним относятся ионы элементов с ат. номером 2, потерявшие все электроны, кроме одного: He+, Li+2, В+3 и т.п. (Они обладают сходными оптич. св-вами)

39. Энергетические уровни: Энергетическим уровнем называется значение энергии, которой обладает электрон в атоме. Энергетическое состояние атома водорода определяется тем, какой энергетический уровень занимает его электрон. (Сами энергетические уровни, и переходы между ними впервые были объяснены с помощью постулатов Бора (знать постулаты!!!!!!).

40. Главное, орбитальное и магнитное квантовые числа: Энергетическое состояние отдельного электрона в атоме описывается 3-мя (4-мя + спиновое) квантовыми числами:

1) главное квантовое число n=1, 2, 3… указывает на квантованность(дискретность)энергии электрона в атоме: а также определяет номер электронной оболочки атома.
2) орбитальное квантовое число =1, 2, 3, 4… (n-1) указывает на квантованность механического орбитального момента импульса электрона в атоме: орбитальное квантовое число характеризует форму электронного облака.

3) магнитное квантовое число m определяет состояние электрона различающиеся целочисленными значениями проекций орбитальных моментов на направление z магнитного поля:

Где Магнитное квантовое число показывает число возможных ориентаций орбитального момента т.е. возможные ориентации электронного облака в пространстве относительно направления магнитного поля.

Пространственным квантованием называется дискретное изменение ориентации орбитального момента относительно магнитного поля.

41. Спектры водородоподобных атомов: Без понятия вообще…Скорее всего такие же, как и у водородного атома.

42. Молекула водорода: Моле́кулаводоро́да — простейшая молекула, состоящая из двух атомов водорода.Н.Бор дал описание модели молекулы водорода, согласно которой, два внешних электрона, образующих молекулу, вращаются по одной и той же орбите вокруг линии, проходящей через ядра обоих атомов, и удерживают последние на определённом расстоянии друг от друга.(не уверен, что это то, что нужно)

43. Молекулярные спектры: Молекулярные спектры - спектры поглощения, испускания или рассеяния, возникающие при квантовых переходах молекул из одного энергетич. состояния в другое.Молекулярные спектры определяются составом молекулы, её структурой, характером хим. связи и взаимодействием с внешними полями.

Элементы физики ядра

44. Строение атомного ядра: (Начать нужно с Резерфорда (планетарной модели атома)а потом…) В современном свете атомное ядро представляет собой сложную систему, которая состоит из элементарных частиц: положительно заряженных протонов(р), и электрически нейтральных нейтронов(n). Протоны и нейтроны называют – нуклоны. Ядро обозначается так: , где Х – символ хим. элемента; Z – атомное номер, равный числу протонов в ядре, и совпадающий с порядковым номером хим. элемента; А – массовое число, равное общему числу нуклонов в ядре, A=Z+N, т.е. Сумма числа протонов и нейтронов в ядре. Атомные ядра называют – нуклиды.

45. Модели ядра: Капельная модель - Эта простейшая модель была предложена М. Борном. В ней атомное ядро рассматривается, как капля заряженной несжимаемой жидкости с очень высокой плотностью (~ 1014 г/см3).

Оболочечная модель - Эта модель является более реалистичной. В данной модели считается, что каждый нуклон движется в усредненном поле остальных нуклонов ядра. В соответствии с этим имеются дискретные энергетические уровни, заполненные нуклонами с учетом принципа Паули. Эти уровни группируются в оболочки, в каждой из которых может находиться определенное число нуклонов. Полностью заполненные оболочки образуют особо устойчивые структуры.Таковыми являются ядра, имеющие, в соответствии с опытом, число протонов, либо нейтронов (либо оба эти числа) 2, 8, 20, 28, 50, 82, 126. (Сомневаюсь на счет этого вопроса, врятли он такое давал!)

46. Природа ядерных сил: Ядерные силы – это силы притяжения, которые удерживают нуклоны (протоны и нейтроны) внутри ядра. Ядерные силы – это не электрические силы, так как они действуют не только между заряженными протонами, но и между незаряженными нейтронами. Область действия ядерных сил очень мала(a=(1÷2)·10^-13).При больших расстояниях действие ядерных сил не проявляется. До расстояний порядка 10-12 см действуют только электромагнитные силы, например между двумя протонами. И лишь на расстоянии порядка 10-13 см над кулоновским отталкиванием начинает преобладать ядерное притяжение.Ядерные силы очень интенсивные, в области своего действия они в 100‑1000 раз больше сил электрического взаимодействия.

47. Радиоактивность: Радиоактивност ь – самопроизвольное превращение атомных ядер некоторых хим. элементов в другие ядра, сопровождающиеся испусканием радиоактивного излучения – элементарных частиц (электронов, фотонов), или ядер ().
Радиоактивность присущая существующим в природных условиях нестабильным изотопам, называется естественной радиоактивностью. Искусственная радиоактивность наблюдается у некоторых изотопов, полученных в результате ядерной реакции. Все нестабильные ядра принято называть радионуклидами, или радиоактивными изотопами. Вещество, содержащее радионуклиды, называют радиоактивным. Распад – процесс самопроизвольного радиоактивного превращение ядер.

48. Закон радиоактивного распада: Радиоактивный распад – спонтанный процесс с участием большого числа радиоактивных ядер. Основной закон радиоактивного распада – :число радиоактивных(не распавшихся) ядер 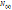убывает со временем по экспоненциальному закону.