Абсолютные величины – показатели, которые выражают размеры общественных явлений и процессов числом единиц совокупности.
Относительные величины – показатели, выражающие количественные соотношения численностей или величин признаков изучаемых явлений.
Виды относительных величин:
1) Относительная величина выполнения плана:
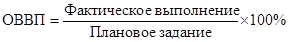
2) Относительная величина планового задания:

3) Относительная величина динамики:

4) Относительная величина структуры:

5) Относительная величина сравнения отражает соотношение двух объемов или уровней в пространстве: соотношение производства автомобилей в Украине и России, соотношение уровней оплаты труда в разных хозяйствах, соотношение уровней производительности на разных предприятиях отрасли и т. д.
6) Относительная величина координации получается посредством деления друг на друга разноименных исходных показателей, она дает типичную характеристику соотношения одно-порядковых по значимости исходных показателей, во-первых, непосредственно связанных между собой, во-вторых, обладающих некоторой общностью.
7) Относительная величина интенсивности:

Задача 5
Имеются следующие данные розничного товарооборота:
Таблица № 2
| Универмаги | Розничный товарооборот (млн. руб.) | ||
| Фактически за базисный год | Отчетный год | ||
| По плану | Фактически | ||
| «Крым» | |||
| «Центральный» |
Определить:
1. Относительную величину выполнения плана.
2. Относительную величину планового задания.
3. Относительную величину динамики.
Статистическая задача - Средние и структурные средние величины.
Теория по решению статистической задачи:
Средние величины – это показатели. Выражающие типичные черты и дают обобщающую количественную характеристику уровня признака по совокупности однородных явлений.
1. Средняя арифметическая:


2. Средняя гармоническая:
3. Средняя квадратическая:

4. Средняя хронологическая:

5. Средняя геометрическая:

К1, К2, К3 и Кn – коэффициенты динамики по отношению к предыдущему периоду.
6. мода интервальных рядов распределения вычисляется по следующей формуле:

х0 – минимальная граница модального интервала;
i – величина интервала;
f2 – частота модального интервала;
f1 – частота интервала, предшествующего модальному;
f3 – частота интервала, следующего за модальным.
Мода для дискретных рядов распределения – это наиболее часто встречающаяся величина признака в данной совокупности.
7. Медиана для интервальных рядов распределения вычисляется по формуле:

x0 – нижняя граница медианного интервала;
i – величина медианного интервала;
∑f – сумма частот ряда;
SМЕ-1 – сумма накопленных частот, предшествующих медианному интервалу;
fМЕ – частота медианного интервала.
Чтобы определить медиану в дискретном вариационном ряду. Необходимо сумму частот разделить пополам и к полученному результату добавить ½.
Типовая задача № 6
Имеются следующие данные о заработной плате рабочих:
Таблица № 1
| Месячная заработная плата (руб) (х) | Число рабочих (f) | х*f |
| х1=120 | ||
| х2=145 | ||
| х4=200 | ||
| х5=208 | ||
| х6=250 | ||
| х7=337 | ||
| Итого |
Определите среднюю заработную плату одного рабочего.