Тема 1. Случайные события. Понятие вероятности. Комбинаторика

Раздел I. ТЕОРИЯ ВЕРОЯТНОСТЕЙ

1.1.Основные фор­мулы комбинаторики. Перестановки, размещения, сочетания.

Прежде, чем перейти к вероятностным задачам, рассмотрим некоторые сведения из комбинаторики. Рассмотренные здесь комбинаторные схемы позволят в дальнейшем решать вероятностные задачи.

Рассмотрим простейшие понятия, связанные с выбором и расположением некоторого множества объектов.

Подсчет числа способов, которыми можно совершить эти действия, часто производится при решении вероятностных задач.

Определение. Размещением из n элементов по k (k £ n) называется любое упорядоченное подмножество из k элементов множества, состоящего из n различных элементов.

Пример 1. Следующие последовательности цифр являются размещениями по 2 элемента из 3 элементов множества {1;2;3}: 12, 13, 23, 21, 31, 32.

Заметим, что размещения отличаются порядком входящих в них элементов и их составом. Размещения 12 и 21 содержат одинаковые цифры, но порядок их расположения различен. Поэтому эти размещения считаются разными.

Число различных размещений из n элементов по k обозначается 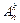и вычисляется по формуле:

,

где n! = 1∙2∙...∙(n - 1)∙ n (читается «n – факториал»).

Число двузначных чисел, которые можно составить из цифр 1, 2, 3 при условии, что ни одна цифра не повторяется равно: .

Определение. Перестановками из n элементов называются такие размещения из n элементов, которые различаются только расположением элементов.

Число перестановок из n элементов P_n вычисляется по формуле: P_n = n!

Пример 2. Сколькими способами могут встать в очередь 5 человек? Количество способов равно числу перестановок из 5 элементов, т.е.

P ₅=5!=1∙2∙3∙4∙5=120.

Определение. Если среди n элементов k одинаковых, то перестановка этих n элементов называется перестановкой с повторениями.

Пример 3. Пусть среди 6 книг 2 одинаковые. Любое расположение всех книг на полке - перестановка с повторениями.

Число различных перестановок с повторениями (из n элементов, среди которых k одинаковых) вычисляется по формуле: .

В нашем примере число способов, которыми можно расставить книги на полке, равно: .

Определение. Сочетаниями из n элементов по k называются такие размещения из n элементов по k, которые одно от другого отличаются хотя бы одним элементом.

Число различных сочетаний из n элементов по k обозначается и вычисляется по формуле: .

По определению 0!=1.

Для сочетаний справедливы следующие свойства:

1. 3.

2. 4.

Пример 4. Имеются 5 цветков разного цвета. Для букета выбирается 3 цветка. Число различных букетов по 3 цветка из 5 равно: .

1.2.Случайные события: событие, виды случайных собы­тий, вероятность событий

Познание действительности в естественных науках происходит в результате испытаний (эксперимента, наблюдений, опыта).

Испытанием или опытом называется осуществление какого-нибудь определенного комплекса условий, который может быть воспроизведен сколь угодно большое число раз.

Случайным называется событие, которое может произойти или не произойти в результате некоторого испытания (опыта).

Таким образом, событие рассматривается как результат испытания.

Пример 1. Бросание монеты – это испытание. Появление орла при бросании – событие.

Наблюдаемые нами события различаются по степени возможности их появления и по характеру их взаимосвязи.

Событие называется достоверным, если оно обязательно произойдет в результате данного испытания.

Пример 2. Получение студентом положительной или отрицательной оценки на экзамене есть событие достоверное, если экзамен протекает согласно обычным правилам.

Событие называется невозможным, если оно не может произойти в результате данного испытания.

Пример 3. Извлечение из урны белого шара, в которой находятся лишь цветные (небелые) шары, есть событие невозможное. Отметим, что при других условиях опыта появления белого шара не исключается; таким образом, это событие невозможно лишь в условиях нашего опыта.

Далее случайные события будем обозначать большими латинскими буквами A,B,C... Достоверное событие обозначим буквой W, невозможное – Ø.

Два или несколько событий называются равновозможными в данном испытании, если имеются основания считать, что ни одно из этих событий не является более возможным или менее возможным, чем другие.

Пример 4. При одном бросании игральной кости появление 1, 2, 3, 4, 5 и 6 очков - все это события равновозможные. Предполагается, конечно, что игральная кость изготовлена из однородного материала и имеет правильную форму.

Два события называются несовместными в данном испытании, если появление одного из них исключает появление другого, и совместными в противном случае.

Пример 5. В ящике имеются стандартные и нестандартные детали. Берем на удачу одну деталь. Появление стандартной детали исключает появление нестандартной детали. Эти события несовместные.

Несколько событий образуют полную группу событий в данном испытании, если в результате этого испытания обязательно наступит хотя бы одно из них.

Пример 6. События из примера 2.4. образуют полную группу равновозможных и попарно несовместных событий.

Два несовместных события, образующих полную группу событий в данном испытании, называются противоположными событиями.

Если одно из них обозначено через A, то другое принято обозначать через (читается «не A »).

Пример 7. Попадание и промах при одном выстреле по цели - события противоположные.