Метод Фурье для уравнения свободных
Колебаний струны
Метод Фурье или метод разделения переменных является одним из наиболее распространенных методов решения уравнений в частных производных. Изложение этого метода мы проведем для задачи о свободных колебаниях струны, закрепленной на концах. Эта задача, как было показано в п. 1.24, сводится к решению однородного уравнения
| (1.132) |
при однородных граничных условиях
 , 
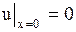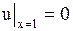
| (1.133) |
и начальных условиях
 ,  ,  .
| (1.134) |
Выделим две части метода Фурье. Первая часть заключается в отыскании частных решений уравнения (1.132), удовлетворяющих граничным условиям (1.133). Вторая часть - нахождение общего решения и удовлетворение начальным условиям (1.134).
Будем искать частные решения (1.132), не равные тождественно нулю, в виде произведения двух функций
 ,
| (1.135) |
удовлетворяющие граничным условиям (1.133).
Дифференцируя дважды выражение (1.135) по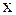 
и по 
, получим
, 
.
Подставляя найденные производные в уравнение (1.132), получим
или, деля обе части равенства на 
,
.
Последнее равенство, левая часть которого зависит от , а правая - только от 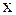, возможно лишь в том случае, когда обе части его не зависят н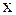и от ни от , т.е. представляют собой одну и ту же постоянную. Обозначим эту постоянную через 
(Знак числа 
будет обоснован ниже). Итак, имеем
 .
| (1.136) |
Из равенства (1.136) получим два обыкновенных дифференциальных уравнения
 ,
| (1.137) |
 .
| (1.138) |
Таким образом, уравнение (1.132) распалось на два уравнения, из которых одно содержит функцию только от , а другое - функцию только от 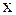или, как говорят, в уравнении (1.132) переменные разделились.
|
|
Поскольку мы ищем решения вида (1.135), удовлетворяющие граничным условиям (1.133), то при любом значении должны соблюдаться равенства
, 
.
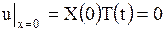Если бы обращался в нуль второй сомножитель (
), то функция 
равнялась бы нулю при всех значениях 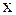и . Такой случай интереса не представляет. Поскольку мы ищем нетривиальные решения, т.е. не равные тождественно нулю, то мы должны считать, что
 и  .
| (1.139) |
Для определения функции 
мы пришли к следующей краевой задаче для обыкновенного дифференциального уравнения: найти такие значения параметра , при которых существуют нетривиальные решения уравнения (1.138), удовлетворяющие граничным условиям (1.139). Эту задачу называют задачей Штурма-Лиувилля.
Те значения параметра , при которых задача (1.138) - (1.139) имеет нетривиальные решения, называются собственными значениями, а сами эти решения - собственными функциями.
Найдем теперь собственные значения и собственные функции задачи (1.138) - (1.139). Нужно рассмотреть три случая, когда 
, 
и 
.
Уравнение (1.138) есть линейное однородное уравнение 2-го порядка с постоянными коэффициентами. Для его решения надо составить характеристическое уравнение
;
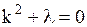отсюда 
, следовательно, вид решения зависит от знака .
А. Пусть . Тогда корни характеристического уравнения действительны и различны и общее решение уравнения (1.138) имеет вид
.
Удовлетворяя граничным условиям (1.139), получим
Так как определитель этой однородной системы
,
то, как известно, система имеет единственное решение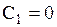 
и 
. Следовательно, 
.
Таким образом, в этом случае решений, отличных от нуля, не существует.
|
|
Б. Пусть . Тогда оба корня характеристического уравнения равны нулю и
.
Граничные условия (1.139) дают:
Отсюда 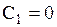, и, следовательно, .
В. Пусть . Корни характеристического уравнения мнимые (
) и решение уравнения (1.138) имеет вид
.
Удовлетворяя условиям (1.139), получим
Из первого уравнения следует, что 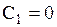, а из второго следует, что 
. Последнее равенство возможно, когда 
, ибо в противном случае . Поэтому
,
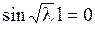откуда определяем 
, где 
- любое целое число 
.
Следовательно, нетривиальные решения задачи (1.138) - (1.139) возможны лишь при значениях
 .
| (1.140) |
Решение, отвечающее фиксированному значению , обозначим через 
. Оно имеет вид
.
Для дальнейшего можем положить 
.
Итак, собственным значениям 
соответствуют собственные функции
 ,  .
| (1.141) |
Заметим, что в соотношениях (1.140), (1.141) мы ограничились только положительными значениями для , так как отрицательные значения не дают новых решений.
Обратимся теперь к отысканию функций 
. Каждому собственному числу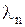 
будет соответствовать свое решение уравнения (1.137), которое обозначим через 
. Для функции имеем уравнение
.
Общее решение этого уравнения имеет вид
,
где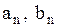 
- произвольные постоянные.
Таким образом, функция
 ,
| (1.142) |
, удовлетворяет уравнению (1.132) и граничным условиям (1.133) при любых 
и 
.
Перейдем ко второй части метода Фурье.
При помощи собственных функций построим решения, удовлетворяющие начальным условиям (1.134).
Возьмем общее решение уравнения (1.142) в виде ряда
 .
| (1.144) |
Если ряд (1.144) сходится равномерно в области 
, 
, то сумма его является непрерывной функцией в этой области. В силу однородности и линейности уравнения (1.132) ряд (1.144) будет также решением, если его можно почленно дифференцировать по 
и по . Действительно, при указанных условиях получим
|
|
,
так как функции 
удовлетворяют уравнению (1.132).
Далее, поскольку каждое слагаемое в (1.144) удовлетворяет граничным условиям (1.133), то этим условиям будет удовлетворять и сумма ряда, т.е. функция . Остается определить постоянные и так, чтобы функция (1.144) удовлетворяла начальным условиям.
Продифференцируем ряд (1.144) по :
 .
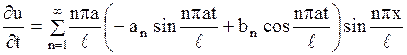| (1.145) |
Подставляя 
в (1.144) и (1.145), получим в силу начальных условий (1.134):
| (1.146) |
Формулы (1.146) представляют собой разложение заданных функций 
и 
в ряд Фурье по синусам на интервале 
.
Из теории рядов Фурье известно, что всякая функция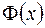 
, непрерывная на отрезке вместе со своей производной первого порядка и удовлетворяющая условию 
, разлагается в абсолютно и равномерно сходящийся ряд Фурье по синусам:
,
где
.
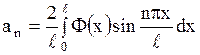Предполагая, что функции и удовлетворяют указанным условиям, мы можем утверждать, что и - коэффициенты Фурье, которые вычисляются по известным формулам:
 ,
| (1.147) |
,
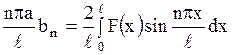откуда
 .
| (1.148) |
Таким образом, ряд (1.144), в котором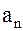 
и вычисляются по формулам (1.147), (1.148), дает решение смешанной краевой задачи (1.132)…(1.134).
РЕШЕНИЕ НЕКОТОРЫХ КРАЕВЫХ ЗАДАЧ МЕТОДОМ ФУРЬЕ. РЕШЕНИЕ УРАВНЕНИЙ КОЛЕБАНИЙ МЕТОДОМ ФУРЬЕ
Метод Фурье или метод разделения переменных, широко используемый при решении ряда задач математической физики, состоит в следующем. Искомая функция, зависящая от нескольких переменных, ищется в виде произведения функций, каждая из которых зависит лишь от одной переменной. После подстановки этого произведения в исходное уравнение получается несколько обыкновенных дифференциальных уравнений, часть из которых вместе с краевыми условиями исходной задачи являются краевыми задачами, называемыми задачами Штурма- Лиувилля. Искомое решение представляется рядом по произведениям собственных функций задач Штурма- Лиувилля. Приведем с х е м у э т о г о м е т о д а для простейших уравнений гиперболического и параболического типов – волнового уравнения и уравнения теплопроводности.