Общим решением уравнения (7.3) является функция

. (7.5)

Проанализируем (7.5), воспользовавшись граничными условиями (7.2). Из условия следует, что , из условия вытекает, чт , (7.6)

и при из (7.6) получаем, что и, следовательно,

. (7.7)

Так как и , то и : , 2, 3…

Таким образом, решение уравнения Шредингера в области II имеет вид:

. (7.8)

Сопоставляя выражения (7.4) и (7.7), найдем возможные значения энергии частицы:

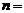; 1, 2, 3 (7.9)

Выражение (7.9) является условием квантования энергии частицы. Из него следует, что существует некоторая минимальная энергия, не равная нулю:

; (7.10)

она соответствует основному состоянию движения частиц. Волновая функция этого состояния, как следует из (7.8),

(7.11)

ни в какой точке внутри ямы в нуль не обращается; она может быть равной нулю лишь на границах ямы.

Из (7.10) видно, что с уменьшением ширины ямы минимальная энергия растет. Следовательно, уменьшение пространства локализации частиц неизбежно сопровождается возрастанием их энергии. Это одно из проявлений принципа неопределенностей.

С учетом того, что частица может находиться лишь внутри ямы, условие нормировки волновой функции примет вид:

или, с учетом (7.8),

.

Из этого условия найдем нормирующий множитель: .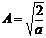

Таким образом, волновая функция имеет вид:

. (7.12)

Выражение (7.12) представляет систему собственных функций, соответствующих возможным состояниям частицы в бесконечно глубокой потенциальной яме. Эти функции обращаются в нуль, , как на границах потенциальной ямы, так и в узловых точках внутри нее, значения координаты которых определяются из условия .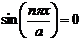

 

20.Прох-е частицей прямоуг. одном. потец. барьера В областях 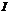и III потенциальная энергия равна нулю: ( £ £0) = 0.

В области (0 < < ) потенциальная энергия = .

Именно эта область является потенциальным барьером.

Состояние движения частицы характеризуется коэффициентами отражения и прохождения , которые имеют смысл вероятности того, что частица останется в области пространства I (коэффициент R) или перейдет в область Ш (коэффициент D).

Рассмотрим случай, когда < 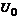, и найдем для частицы коэффициенты отражения и прохождения . Для этого необходимо решить одномерное стационарное уравнение Шрёдингера и найти функции состояния , и в каждой из областей пространства , , .

 

( £ £ ) = 0.

Уравнение Шрёдингера для областей , , соответственно имеет вид:

;

, ; (8.1)

, .

 

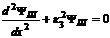Решение уравнения для области имеет вид

, (8.2)

и описывает падающую волну де Бройля с амплитудой и отраженную волну с амплитудой . Решение в области III содержит только прошедшую волну, распространяющуюся в положительном направлении оси :

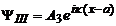. (8.3)

 

В области П общее решение уравнения Шрёдингера имеет вид

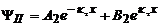. (8.4)

21.Прозрачность потец. барьера приз-ой формы. Если потенциальный барьер имеет произвольную форму (рисунок 8.2), то его можно представить как последовательность прямоугольных потенциальных ба

рьеров. Коэффициент прохождения такого барьера в этом случае приблизительно равен произведению коэффициентов прохождения через все прямоугольные потенциальные барьеры, которыми он моделируется. Числовой множитель перед экспонентой в (8.15) при плавном изменении потенциальной энергии является медленно меняющейся функцией. Таким образом, для потенциального барьера произвольной формы коэффициент прозрачности определяется

. (8.16)

Описанные в данном разделе особенности поведения частиц связаны с их корпускулярно-волновой природой. Туннельный эффект существен лишь для

 

систем, имеющих микроскопические размеры и массы. Чем уже потенциальный барьер и чем меньше разность , тем больше вероятность прохождения частицы через барьер.

22. Тунельный эфф-т. Холодная эмиссия элект. Преодоление микрочастицей потенциального барьера в случае, когда ее полная энергия меньше высоты барьера, называется туннельным эффектом, или туннелированием. Примером проявления туннельного эффекта в атомной физике могут служить автоионизация атома в сильном электрическом поле и ионизация атома в поле сильной электромагнитной волны.

Туннельный эффект лежит в основе альфа-распада радиоактивных ядер. Без туннельного эффекта было бы невозможно протекание термоядерных реакций: кулоновский потенциальный барьер, препятствующий необходимому для синтеза сближению ядер-реагентов, преодолевается частично благодаря высокой скорости (высокой температуре) таких ядер, а частично - благодаря туннельному эффекту.

Особенно многочисленны проявления туннельного эффекта в физике твердого тела. Туннельным эффектом объясняется холодная эмиссия электронов из металла. Электроны удерживаются внутри металла силами притяжения, и для удаления электрона из металла необходимо совершить определенную работу. Это означает, что потенциальная энергия электрона вне металла больше, чем внутри него, причем на границе металл – вакуум потенциальная энергия резко возрастает. Если вблизи поверхности металла создано электрическое поле с напряженностью порядка 10⁸ В/м, электроны покидают поверхность металла. Это явление называется холодной эмиссией.

Классическая физика не может объяснить это явление: электрическое поле в металл не проникает и изменяет потенциальную энергию лишь вне металла (штриховая линия на рисунке 8.3). Чтобы покинуть металл, электроны должны преодолеть потенциальный барьер.

Поскольку их энергия меньше высоты барьера , то с классической точки зрения электроны не могут выйти за пределы поверхности. В соответствии с квантовой механикой коэффициент прохождения электронов через барьер определяется интегралом

здесь (где – напряженность электрического поля), ), Тогда значение интеграла определяется следующим образом:

,

где В/м. Так как ток эмиссии пропорционален коэффициенту прохождения барьера, то в соответствии с формулой (8.16) зависимость плотности тока эмиссии от напряженности электрического поля должна иметь вид:

.Такая зависимость хорошо подтверждается экспериментом.

23. Средние знач-я и опер-ры физ величин. Т.к. квантовомеханическое описание состояния частицы носит статистический (вероятностный) характер, особое значение имеют средние значения физических величин. Рассмотрим правила определения средних значений и явного вида операторов физических величин, которые необходимы для описания состояний электрона в атоме и атомной системы как целого.

Среднее значение величины из достаточно большого числа измерений определяется следующим образом:

. (6.1)

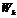В теории вероятностей среднее значение величины , принимающей значения ( 1, 2, 3, …) с вероятностями , находят по формуле

(6.2)

Как было указано выше (смотри формулу (5.6), стационарное состояние частицы в квантовой механике описывается функцией . То есть плотность вероятности обнаружить частицу в окрестности точки определяется ее координатной частью:

.

Воспользуемся формулой (6.2) и определим среднее значение координаты частицы в одномерном случае.

.

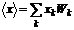Учитывая, что при квантово-механическом описании координате , а также ее функциям сопоставляется оператор умножения ( и ,соответственно), можно записать, переходя к пределу,

. (6.3)

Этот результат можно обобщить на случай многомерного пространства:

, (6.4)

где – элементарный объем в – мерном пространстве.

Среднее значение физической величины, являющейся функцией координат, определяется аналогичным образом

. (6.5)

По аналогии с (6.3) запишем формулу для определения среднего значения импульса частицы в одномерном пространстве:

, (6.6)

где – плотность вероятности того, что частица имеет значение проекции импульса , а интегрирование проводится по всему импульсному пространству. Но поскольку функция нам неизвестна, необходимо перейти от импульсного пространства к координатному, в котором плотность вероятности определяется функцией состояния, являющейся решением известного нам уравнения Шредингера. Для этого воспользуемся преобразованием Фурье, и выражение (6.6) примет вид:

, (6.7)

Где (6.8)

– оператор импульса частицы в одномерном пространстве.

Проводя обобщение на случай многомерного пространства получим для определения среднего значения любой величины, зависящей от координат и импульсов, следующее выражение:

.(6.9)

Здесь

– оператор функции ,

– элементарный объем в -мерном пространстве.

Это правило может быть обобщено: среднее значение физической величины, представленной оператором 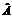, в состоянии, характеризуемом функцией , определяется формулой

. (6.10)

Таким образом, для вычисления среднего значения физической величины достаточно знать -функцию состояния частицы и явный вид изображающего эту величину оператора.

Воспользуемся формулой (6.8) и, перейдя к трехмерному пространству, найдем, что

, ,

и оператор импульса в трехмерном пространстве имеет вид:

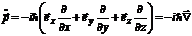, (6.11)

где , , – орты декартовой системы координат.

Определим вид оператора Гамильтона . В классической физике функцией Гамильтона называется функция полной энергии, выраженная через импульсы и координаты частиц. Для частицы массы в нерелятивистском приближении полная энергия равна сумме кинетической и потенциальной энергий:

. (6.12)

В квантовой механике функции Гамильтона должен соответствовать оператор, вид которого определяется в соответствии с постулатом 7 (смотри лекцию 5) следующим образом:

. (6.13)

После подстановки в (6.13) вместо импульса 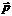его оператора (6.11), получим:

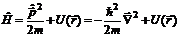. (6.14)

Явный вид оператора Гамильтона зависит от решаемой задачи, содержание которой конкретизирует вид функции .

Наряду с энергией важнейшей характеристикой движения электрона относительно ядра в атоме является орбитальный момента импульса. В классической механике момент импульса частицы определяется как векторное произведение радиус-вектора частицы на ее импульс :

,или в проекциях на оси координат:

 

В квантовой механике проекциям момента импульса , , ставятся в соответствие операторы

(6.15)

В сферических координатах выражениям (6.15) соответствуют

24. У р-е для опред-я собств-го сост-ия опер-ра физ. велечины. Собственные функции оператора определяются из уравнения

и имеют вид:

. (6.17)

Из требования однозначности функции следует, что она должна быть периодической с периодом . Тогда

 

, 0, , , …. (6.18)

Для операторов выполняются следующие перестановочные (коммутационные) соотношения:

 

; ; , (6.19)

из которых следует, что проекции орбитального момента связаны соотношениями неопределенностей вида

,

где и - неопределенности (дисперсии) измеряемых значений физических величин и .

Для оператора

(6.20)

с учетом формулы (6.16) можно получить выражение

, (6.21)

в котором

(6.22)

- оператор Лежандра.

Несложно убедиться, что оператор коммутирует с каждым из операторов :

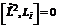; , , . (6.23)

Следовательно, операторы и 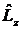имеют общую систему собственных функций, которые могут быть найдены из системы уравнений:

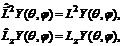(6.24)

записанных в сферической системе координат.

Собственные значения оператора определяются из уравнения (6.24) в виде

, 1, 2, …. (6.25)

При этом собственными функциями для операторов и 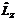являются сферические функции

, (6.26)

образующие полную систему ортонормированных функций (здесь – присоединенный полином Лежандра, - нормировочный множитель).

25.Стац. УШ для водор-ых с-м. Запишем стационарное уравнение Шрёдингера для электрона, имеющего в поле ядра потенциальную энергию :

(9.1)

(здесь - масса электрона).

Поместим ядро, заряд которого , в начало системы координат. Потенциальная энергия электрона, находящегося на расстоянии от ядра, определяется выражением

, (9.2)

где (в системе СИ), (в системе СГС)

Так как функция сферически симметрична (), то уравнение (9,1) целесообразно решать в сферических координатах, считая . Физический смысл имеют решения, удовлетворяющие стандартным условиям, то есть функции, однозначные, конечные, непрерывные и гладкие во всей области изменения переменных (, , .

26. Решение УШ для радиал-ой ф-ии водор-ых с-м. Собственную функцию представим в виде:

(9.6)

и поставим перед собой задачу найти вид радиальной функции , выделяя в уравнении (9.3) лишь радиальную составляющую оператора Лапласа. Такая постановка задачи позволяет получить лишь часть решений для собственной функции, а именно, для состояний электрона с нулевым моментом импульса. Интерес к поставленной задаче обусловлен тем, что ее решение дает возможность получить полную информацию о спектре собственных значений энергии.

Получим одномерное стационарное уравнение Шредингера, имеющее вид

(9.7)

Для решения уравнения (9.7) сделаем замену

. (9.8)

Найдем первую и вторую производные функции , подставим полученные выражения, а также (9.8) в уравнение (9.7) и после приведения подобных членов получим:

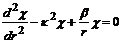. (9.9)

Простой анализ показывает, что при 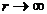уравнение (9.9) имеет вид:

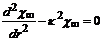. (9.10)

Общий вид решения этого уравнения хорошо известен:

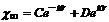. (9.11)

При второе слагаемое в (9.11) неограниченно растет. Считая , удовлетворим условию конечности собственной функции и получим:

. (9.12)

Функция (9.12) применима только при . Для того, чтобы найти вид функции , при любых удовлетворяющей стандартным требованиям, представим ее в виде:

. (9.13)

Взяв первую и вторую производные от функции (9.13), подставим их и саму функцию (9.13) в уравнение (9.9). После несложных преобразований имеем:

. (9.14)

Запишем сумму коэффициентов при в уравнении (9.14):

. (9.15)

Из (9.15) следует:

. (9.16)

Выражение (9.16) – это рекуррентная формула для коэффициентов используемого ряда. Исследуем поведение ряда при (то есть при бесконечно большом числе членов в нем). Тогда (9.16) переходит в формулу

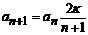. (9.17)

Но выражение (9.17) есть не что иное, как рекуррентная формула ряда, в который разлагается функция . Следовательно, не ограничивая число членов ряда, получим функцию, которая с точностью до постоянного множителя имеет вид:

.

Как следует из (9.8) и (9.13), при эта функция неограниченно растет.

Для того, чтобы радиальная функция 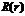оставалась конечной при любых , необходимо, чтобы ряд обрывался, то есть переходил в сумму конечного числа членов. Оборвем ряд, например, на -члене. Для этого потребуем, чтобы и все последующие коэффициенты обращались в нуль. Это требование выполняется, как следует из (9.16), при условии

. (9.18)

Тогда имеющая физический смысл радиальная функция с точностью до постоянного множителя запишется в виде:

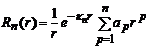, (9.19)

где определяется из уравнения (9.18):

. (9.20)

Принимая во внимание (9.4) и (9.5), приходим к выводу, что (9.20) определяет возможные значения энергии

, (9.22)

при которых радиальная функция имеет вид (9.19).

Формула (9.22) определяет дискретный спектр энергии для электрона в водородоподобном атоме, то есть выражает правило квантования энергии. При заданном значении , называемом главным квантовым числом, энергия электрона принимает конкретное значение, то есть имеем определенный энергетический уровень.

Видим, что выражение (9.22) полностью совпадает с формулой для полной энергии электрона на n- ой орбите в теории Бора для водородоподобных систем (смотри (3.11)). Для обсуждения спектральных закономерностей для рассматриваемых атомных систем удобно воспользоваться схемой энергетических уровней (смотри рисунок 3.1), изобразив на ней в соответствии в правилом частот Бора разрешенные переходы, то есть переходы, вероятность которых отлична от нуля. Правила, показывающие изменения квантовых чисел, соответствующие разрешенным переходам, называются правилами отбора. Для их установления в квантовой механике достаточно знать волновые функции исходного и конечного состояний атома и оператор перехода (оператор электромагнитного взаимодействия).

При переходах электрона из одного состояния в другое для квантового числа должно выполняться следующее правило отбора:

– любое целое число.

В соответствии с этим правилом в спектрах излучения водородоподобных атомов на уровень с будут разрешены переходы с любого уровня, для которого > 1 (серия Лаймана), на уровень с – с любого уровня, для которого > 2 (серия Бальмера), и т.д.

27. УШ для водор-ых с-м и его реш-е в общем случае. Рассмотрим решение уравнения Шредингера для водородоподобной системы

. (10.1)

в общем случае.

Уравнение (10.1) решим методом разделения переменных, для чего собственную функцию представим в виде:

. (10.2)

После разделения переменных уравнение (10.1) распадается на два ‒ для радиальной и угловой функций соответственно:

; (10.3)

, (10.4)

где 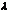– постоянная разделения. Явный вид оператора представлен формулой (6.22).

Проанализируем решение уравнения (10.4). Заметим, что (10.4) не содержит потенциальной энергии , следовательно, результаты его решения имеют универсальный характер и описывают поведение частицы в любом сферически симметричном поле.

Уравнение (10.4) также решаем методом разделения переменных. Полагая

, (10.5)

и считая постоянную разделения переменных равной , для функций и получаем следующие уравнения:

, (10.6)

. (10.5)

Общее решение уравнения (10.6) имеет вид:

.

Удовлетворив требованию однозначности и произведя нормировку, получим в следующем виде:

, , , ,… (10.6)

Отметим, что решение (10.6) полностью совпадает с собственной функцией оператора (смотри (6.17), (6.18)).

Для решения уравнения (10.5) введем новую переменную , после чего вместо (10.5) получим уравнение

. (10.7)

28. Радиальное распре-е элект-а в водор-ом атоме. Уравнение для радиальной составляющей собственной функции (10.13) будем решать по той же логической схеме, что и в рассмотренном выше частном случае (смотри лекцию 9). Решение будем искать в виде

. (10.14)

С учетом (10.14) уравнение (10.13) приобретает вид:

(10.15)

Определим пределы суммирования ряда (10.15), удовлетворяющие физическому смыслу функции . Обозначим и запишем сумму коэффициентов при минимальной степени в многочлене (10.15), то есть при . Получим:

.

Это уравнение имеет два решения:

; .

Проанализируем функцию 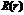(смотри (10.14)) при и .

Взяв , получим:

.

Поскольку , то при функция за счет первого члена ряда. Следовательно, решение не удовлетворяет физическому смыслу волновой функции и должно быть отброшено. Остается

. (10.16)

Вернемся к уравнению (10.15) и запишем сумму коэффициентов при :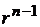

. (10.17)

Из (10.17) следует:

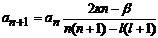. (10.18)

Выражение (10.18) – это рекуррентная формула для коэффициентов используемого ряда. Исследуя поведение ряда при , видим: как и в рассмотренном выше частном случае, сумму ряда необходимо обрывать на некотором n ном члене, чтобы удовлетворить требованию конечности собственной функции во всем пространстве координаты r.

Тогда имеющая физический смысл радиальная функция запишется в виде:

, (10.19)

где определяется из уравнения (9.18):

. (10.20)

Принимая во внимание (9.4) и (9.5), приходим к выводу, что (10.20) определяет возможные значения энергии

, (10.21)

при которых радиальная функция имеет вид (10.19).

Выражение (10.21) определяет дискретный спектр энергии для электрона в водородоподобном атоме и полностью совпадает с формулой квантования энергии, полученной в частном случае.

29.Простр-ое (угловое) распр-е элект-а в водор-ом атоме.В курсе «Методы математической физики» показано, что функция удовлетворяет требованию непрерывности и конечности только при условии

, (10.8)

где .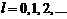

Решение уравнения (10.7) представляет собой, с точностью до нормирующего множителя, присоединенные полиномы Лежандра

. (10.9)

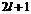При заданном значении число может принимать различных значений:

, , … . (10.10)

С учетом (10.6) и (10.9) угловая функция после нормировки имеет вид:

. (10.11)

Как видно из (10.11), угловая функция определяется квантовыми числами , 1, 2, … и , , … как параметрами.

Обратимся теперь к решению уравнения (10.3). С учетом (9.4) и (10.8) оно принимает вид:

(10.12)

или

. (10.13)

Величина имеет смысл эффективной потенциальной энергии электрона. Здесь первое слагаемое описывает кулоновское взаимодействие электрона и ядра. Добавка обусловлена наличием момента импульса у движущегося относительно ядра электрона ().

Зависимость и составляющих ее компонентов проанализируем, воспользовавшись их графическим изображением (рисунок 10.1).

Как видно из рисунка 10.1, при больших расстояниях в преобладает энергия кулоновского притяжения, при малых - энергия, обусловленная центробежными силами. При энергии электрона <0 его движение происходит в области пространства, огр