Параметры состояния системы. Экстенсивные и интенсивные параметры.

Введение в физическую химию. История развития физической и коллоидной химии.

Возникновение физической химии связано с именем русского ученого Ломоносова. Физическая химия как наука возникла в сер. 18 века. Ломоносов составил первую программу по физической химии и 4 раза в неделю читал лекции для студентов. В 1860 г. Бекетов Н.Н. в Хпрьковском университете читал курс лекции «Взаимосвязь между физическими и химическими явлениями» и в 1865 году назвали эту науку физической химией. В 1887 году впервые открыли в Лейцигском университете открыли кафедру физич.химии и начали выпучкать журналы, это было организовано ученым Оствальдом. Огромную роль для развития физической химии сыграло открытие периодического закона Менделеева Д.И. в 1869 году. В 19 веке физич. химия начала развиваться очень быстро. Физическая химия промежуточная наука между физикой и химией. Физич.химия изучает строение вещества, состояние равновесия хим.процессов, вероятность перехода из одного сост. в другое, зависимость скорости реакции от времени и т.д. Одним из первых наиболее плодотворных для физической зимии методов явл.термодинамический метод.

Коллоидная химия как наука имеет небольшую историю, однако свойства коллоидных систем и коллоидно-химические процессы человек использовал с давних времён. Это, например, такие ремёсла, как получение красок, керамики, глазури, прядение льна, хлопка, шерсти, выделывание кож.

Начиная с XVIII века появляются описания отдельных исследований, позже вошедшие в соответствующие разделы коллоидной химии. К ним относят работы М. В. Ломоносова по кристаллизации, получению цветных стёкол с применением дисперсии металлов (1745—1755 гг.). В 1777 г. К. Шееле и Ф. Фонтана независимо друг от друга обнаружили явление адсорбции газов углём. В 1785 г.Т. Е. Ловиц обнаружил явление адсорбции из растворов. П. Лаплас в 1806 г. получил первые количественные отношения для капиллярного давления. В 1808 г. Ф. Ф. Рейсс, проводя опыты с элементом Вольта, открыл явления электрофорез и электроосмос. Одни из наиболее ранних исследований коллоидных систем выполнены итальянцем Ф. Сельми в 1845 году. Он изучал системы, представляющие собой хлорид серебра, серу, берлинскую лазурь, распределенную в объёме воды. Эти системы, полученные Сельми, очень похожи на истинные растворы, однако Сельми полагал, что ни изученные им, ни другие подобные вещества не могут находиться в воде в виде таких же мелких частиц, как и образующиеся в истинных растворах, то есть в виде отдельных молекул илиионов

. Взгляды, близкие к Сельми, высказывал К. Нэгели, считавший, что в таких системах частицы серы, хлорида серебра и других веществ — более крупные агрегаты, чем отдельные молекулы. Для полимолекулярных агрегатов он ввел понятие «мицелла». Чтобы отличать системы, содержащие мицеллы, от растворов, где растворенное вещество находится в виде отдельных молекул, Нэгели назвал мицеллосодержащие системы «золями». Основоположником коллоидной химии принято считать Т. Грэма, выполнившего в 60-х годах XIX века первые систематические исследования коллоидных систем (золей). Ему же принадлежит и введение термина «коллоид». Впоследствии коллоидная химия включила в себя результаты, полученные в других областях физики и химии, и в конце XIX — начале XX веков сформировалась в самостоятельный раздел химии.

Понятие термодинамики. Системы, виды систем.

Термодинамика – наука о превращении различных видов энергии друг в друга или превращение тепла в движение. Термодинамика происходит от греч.термо- тепло. Зная законы термодинамики, можно предвидеть возможна ли данная реакция при данных условиях или нет. Дюбое тело или группа тел, находящиеся между собой во взаимодействии мысленно или реально отделенных от окружающей среды называется системой. Системя, которые не взаимодействуют с окруж.средой ни массой, ни энергией, называется изолированной, следовательно, сохраняет постоянный объем. Совокупность всех гомогенных частей системы, одинаковых по хим.составу и отделенных от других частей системы поверхностью раздела, называется фазой. Система, в которой есть поверхностный раздел, называется гетерогенной системой. Система, в которой составляющие ее вещества находятся в одной фазе, называется гомогенной системой. Если система обменивается с окружающей средой энергией и массой то назыв .открытой, если есть энергообмен, но нет массы обмена- закрытой системой.

Параметры состояния системы. Экстенсивные и интенсивные параметры.

ПАРАМЕТРЫСОСТОЯНИЯ (от греч. parametron - отмеривающий, соразмеряющий) (термодинамич. параметры, термодинамич. переменные), физ. величины, характеризующие состояние термодинамич. системы в условиях термодинамического равновесия. Различают экстенсивные П.- пропорциональные массе системы, и интенсивные П., не зависящие от массы системы. Экстенсивные П.- объем, температура, давление, концентрация, вязкость, плотность. Интенсивные: объем, масса.

 

4. Процессы и виды процессов. Тепловой процесс (термодинамический процесс) — изменение макроскопического состояния термодинамической системы. Система, в которой идёт тепловой процесс, называется рабочим телом. Тепловые процессы можно разделить на равновесные и неравновесные. Равновесным называется процесс, при котором все состояния, через которые проходит система, являются равновесными состояниями. Тепловые процессы можно разделить на обратимые и необратимые. Обратимым называется процесс, который можно провести в противоположном направлении через все те же самые промежуточные состояния. Можно выделить несколько простых, но широко распространённых на практике, тепловых процессов:

Адиабатический процесс Адиабатический процесс — термодинамический процесс в макроскопической системе, при котором система не получает и не отдаёт тепловой энергии. Адиабатический процесс является частным случаем политропного процесса. Адиабатические процессы обратимы, если их проводить достаточно медленно (квазистатически). В общем случае адиабатический процесс необратим.

Изохорный процесс Изохорический или изохорный процесс — это термодинамический процесс, который происходит при постоянстве объёма. В газах и жидкостях осуществляется очень просто: для этого достаточно нагревать (охлаждать) вещество в сосуде, который не изменяет своего объёма. При изохорическом процессе давление идеального газа прямо пропорциально его температуре.

Изобарный процесс Изобарный — термодинамический процесс, происходящий в системе при постоянном давлении.

Изотермический процесс Изотермический процесс — термодинамический процесс, происходящий в физической системе при постоянной температуре. При изотермическом процессе системе, вообще говоря, сообщается определённое количество теплоты (или она отдаёт теплоту) и совершается внешняя работа.

5. Что обозначает функция состояния системы. Внутренняя энергия - функция состояния системы, т.к. не зависит от пути достижения данного состояния, а зависит только от начального и конечного состояния состемы. Важно термодинамичной функцией является ЭНТАЛЬПИЯ: H=U+pV. Энтальпия – это теплосодержание системы ΔU- полная энергия системы, явл.функцией состояния системы. - уравнение показывает, что энтальпия зависит от характера процесса, а определяется лишь значениями U, р, V в начальном и конечном состоянии, если

6. Максимальная работа расширения идеального газа. Пар или газ, расширяясь, может совершить работу.
При этом внутренняя энергия пара превращается в механическую энергию.
Устройства, в которых внутренняя энергия пара или газа (рабочего тела) превращается в механическую энергию, называются тепловыми двигателями. При нагревании воды в закрытой пробкой пробирке увеличивается количество пара, находящегося под пробкой, и повышается его давление на пробку. Наконец, давление пара выталкивает пробку, при этом пар совершает работу. Часть первоначальной энергии пара пошло на совершение работы по выталкиванию пробки. Внутренняя энергия пара превратилась в механическую энергию. Так как пар выходит еще достаточно горячий, то оставшуюся энергию он отдает окружающему воздуху, имеющему более низкую температуру.

Газ оказывает давление на любую стенку сосуда. Если стенка подвижна (например, поршень на рис. 1), то сила давления F совершит работу A, переместив поршень на расстояние DL.

Если DL невелико, то давление газа останется примерно постоянным. Тогда работа будет равна:

A = F· DL · cosa = P · S · DL,
где S - площадь поршня,
a - угол между направлением силы и перемещением поршня (a= 0).

Произведение S · DL равно изменению объема газа DV от начального V₁ до конечного V₂ значения, т.е. S · DL =DV = V₁- V₂. Тогда

A = P·(V₂ - V₁) = P·DV.

В изобарном процессе расширения газа P = const. Следовательно, при любом сколь угодно большом увеличении объема сила давления газа на поршень будет постоянной, и формула работы сохранит свой вид

A = P·(V₂ - V₁).

7. Первый Закон термодинамики и математическое уравнение. Основан на том, что все формы энергии переходят друг в друга в строго эквивалентных количествах. Форма передачи энергии в виде работы и теплоты. Они могут иметь разные знаки.

1. Если система отдает тепло, то Q имеет положительный знак

2. Если система отдает тепло, то Q имеет отрицательный знак

3. Если система совершает работу, то А обозначается (А>0)

4. Если мы совершили работу над системой, то А<0.

8. Применение 1 закона термодинамики к различным процессам. С помощью первого закона термодинамики можно делать важные заключения о характере протекающих процессов. Рассмотрим различные процессы, при которых одна из физических величин остается неизменной (изопроцессы), например случай, когда система представляет собой идеальный газ.

Изохорный процесс. При изохорном процессе объем газа не меняется, и поэтому работа газа равна нулю. Изменение внутренней энергии газа согласно уравнению (13.11) равно количеству переданной ему теплоты:

Если газ нагревается, то 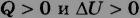, его внутренняя энергия увеличивается. При охлаждении газа 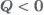и 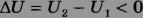, изменение внутренней энергии отрицательно и внутренняя энергия газа уменьшается.
Изотермический процесс. При изотермическом процессе (T =const) внутренняя энергия идеального газа (см. формулу (13.1)) не меняется. Согласно формуле (13.11) все переданное газу количество теплоты идет на совершение работы:

Если газ получает тепло , то он совершает положительную работу 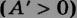. Если, напротив, газ отдает тепло окружающей среде (термостату), то . Работа же внешних сил над газом в последнем случае положительна.
Изобарный процесс. При изобарном процессе согласно формуле (13.11) передаваемое газу количество теплоты идет на изменение его внутренней энергии и на совершение им работы при постоянном давлении:

Адиабатный процесс. Рассмотрим теперь процесс, протекающий в системе, которая не обменивается теплом с окружающими телами. Процесс в теплоизолированной системе называют адиабатным.
При адиабатном процессе Q =0 и согласно уравнению (13.10) изменение внутренней энергии происходит только за счет совершения работы:

 

9) Теплоемкость системы и виды теплоемкости

Количество теплот необходимое для нагревания одной массы вещества на одни градус называется теплоемкостью.

Истинной теплоемкостью называется количество теплоты, необходимая для изменения температуры на одни градус Цельсия, массы одного грамма вещества.

Размерность теплоемкость Дж / моль, кДж

С =С1/м

Средняя теплоемкость – количество тепла необходимое для нагревания одного кг вещества при данном температурном интервале. С=Q/m(T2-T1)

Малярная теплоемкость – тепловая энергия необходимая для повышения температуры одного моля чистого вещества на один градус Цельсия

Теплоемкость одного грамма вещества называется удельной теплоемкостью

СМ=Суд М, где М-малярная масса

 

10) Закон Гесса и вследствие из закона Гесса

Закон Гесса вытекает из первого закона термодинамики и гласит “Тепловой эффект химической реакции зависит от вида и состояния исходных и конечных продуктов,но не зависит от пути процесса. вытекают следующие выводы:

1) Тепловой эффект реакции разложения какого ни будь химического соединения провотиположен по знаку тепловому эффекту его образования (закон Лавуазье-Лапласа)

2H2O=2H2+O2+68317 кал /моль

2H2+O2=2H2O-68317 кал/моль

2) Теплота образования соединения из исходных веществ равна по величине и обратно по знаку теплоте разложения этого соединения из исходных веществ 2H2+O2=2H2O-68317 кал/моль

2H2O=2H2+O2+68317 кал /моль

3)тепловой эффект химической реакции равен разности между сумой теплот образования конечных продуктов из сумы теплот образования исходных веществ с учетом коэффициентов при формулах в уравнение реакции

4)теплотой сгорания соединения называется тепловой эффект реакции сгорания а 1 моль этого соединения до образования СО2 и H2O

CH4+2O2=CO2+2H2O

Тепловой эффект реакции равен сумме теплот сгорания исходных веществ, минус суммы теплота сгорания продуктов реакции

 

11) Виды тепловых эффектов и методы определения их 1)Тепловой эффект реакции разложения какого ни будь химического соединения провотиположен по знаку тепловому эффекту его образования (закон Лавуазье-Лаплаза)

2H2O=2H2+O2+68317 кал /моль

2H2+O2=2H2O-68317 кал/моль

2)Теплота образования соединения из исходных веществ равна по величине и обратно по знаку теплоте разложения этого соединения из исходных веществ 2H2+O2=2H2O-68317 кал/моль

2H2O=2H2+O2+68317 кал /моль

3)тепловой эффект химической реакции равен разности между сумой теплот образования конечных продуктов из сумы теплот образования исходных веществ с учетом коэффициентов при формулах в уравнение реакции

4)теплотой сгорания соединения называется тепловой эффект реакции сгорания а 1 моль этого соединения до образования СО2 и H2O

CH4+2O2=CO2+2H2O

Тепловой эффект реакции равен сумме теплот сгорания исходных веществ, минус суммы теплота сгорания продуктов реакции

 

12) Зависимость теплового эффекта от температуры. Закон Кирхгофа Для того что бы найти тепловой эффект реакции при иной температуры необходимо знать зависимость теплового эффекта от температуры при которой проходит процессТемпературным коэффициентом теплового эффекта называется приращение теплового эффекта соответственному изменению температуры на один градус Цельсия

Изобарный тепловой эффект Δ H, а приращение d(ΔH)

(dΔH\dT)_p при Р-cons (dΔU\dT)_v при V – const

Если внутреннею энергию системы ΔU дифференцировать при V – const при заданной температуре, то

(dΔU\dT)_v = (dΔU₂\dT)_v2=(d ΔU₁\dT)_v1

C_v=dU\dT, C_p=dH\dT

(dΔU\dT)_v=C_v2-C_v1=ΔC

Изобарный тепловой эффект Δ H, его приращение (dΔH)

ΔС_v=∑(nC_vкон)-∑(C_vнач)

Закон Кирхгофа гласит: температурный коэффициент теплового эффекта равен разности суммы теплоемкостей продуктов реакции и суммы теплоемкости исходных веществ

ΔC_p==∑C_pкон-∑C_pнач отсюда

dΔH=ΔС_рdT

13) Тепловой эффект химической реакции. Эндотермическое и экзотермическое реакции. Примеры

Тепловой эффект химической реакции зависит от вида и состояния исходных и конечных продуктов,но не зависит от пути процесса.

Тепловой эффект химической реакции равен разности между сумой теплот образования конечных продуктов из сумы теплот образования исходных веществ с учетом коэффициентов при формулах в уравнение реакции.

Если в результате реакции выделяется теплота, то реакция экзотермическая(-ΔН)если теплота поглощается то реакция эндотермическая(+ΔН)

14) Второй закон термодинамики. Понятие энтропии

Второй закон термодинамики устанавливаетнекоторые общие критерии самопроизвольного и не самопроизвольного изменения системы, а также критерии равновесия. Энтропия является мерой не упорядоченности системы.Абсолютное значение энтропии рассчитано для всех веществ, размерность Дж/моль*К Для энтропии также справедливо: изменение энтропии системы в результате химической реакции, (ΔS)=разности алгебраической суммы энтропии продуктов реакций и алгебраической суммы энтропии исходных веществ. Энтропия веществ зависит от агрегатного состояния. При изменении энтропии выделяется определённое количество тепла. При постоянной температуры для превращения не зависимо от характера процесса величина изменения энтропии постоянно. Энтропия является функцией состояния системы, зависит от конечного и начального состояния системы.

15) Энтропия и термодинамическая вероятность.

Второй закон термодинамики устанавливаетнекоторые общие критерии самопроизвольного и не самопроизвольного изменения системы а также критерии равновесия.Энтропия является мерой не упорядоченности системы.Абсолютное значение энтропии рассчитано для всех веществ, размерность Дж/моль.*К Для энтропии также справедливо:изменение энтропии системы в результате химической реакции, (ΔS)=разности алгебраической суммы энтропии продуктов реакций и алгебраической суммы энтропии исходных веществ. Энтропия веществ зависит от агрегатного состояния. При изменения энтропии выделяется определённое количество тепла.При постоянной температуры для превращения не зависимо от характера процесса величина изменения энтропии постоянна. Энтропия является функцией состояния системы зависит от конечного и начального состояния системы.

16) Математическое уравнение второго закона термодинамики.формулы определения изменение энтропии в различных процессах. Математическое выражение второго закона термодинамики записывается

dS≥dq\dT здесь знак ≥ относится к необратимым, а знак «= «к обратимым

в самопроизвольном процессе dS≥dQ

в равновесном процессе dS=dQ\T

в не самопроизвольном процессе dS меньше dQ\T