От целых показателей степени числа a напрашивается переход к рациональным показателем. Ниже мы определим степень с рациональным показателем, причем будем это делать так, чтобы сохранялись все свойства степени с целым показателем. Это необходимо, так как целые числа являются частью рациональных чисел.
Известно, что множество рациональных чисел состоит из целых и дробных чисел, причем каждое дробное число может быть представлено в виде положительной или отрицательной обыкновенной дроби. Степень с целым показателем мы определили в предыдущем пункте, поэтому, чтобы закончить определение степени с рациональным показателем, нужно придать смысл степени числа a с дробным показателем m/n, где m – целое число, а n - натуральное. Сделаем это.
Рассмотрим степень с дробным показателем вида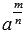 
. Чтобы сохраняло силу свойство степени в степени, должно выполняться равенство 
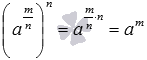. Если учесть полученное равенство 
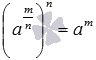и то, как мы определили корень n-ой степени, то логично принять 
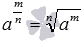при условии, что при данных m, n и a выражение 
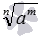имеет смысл.
Несложно проверить, что при 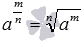справедливы все свойства степени с целым показателем (это сделано в разделе свойства степени с рациональным показателем).
Приведенные рассуждения позволяют сделать следующий вывод: если при данных m, n и a выражение 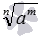имеет смысл, то степенью числа a с дробным показателем m/n называют корень n -ой степени из a в степени m.
Это утверждение вплотную подводит нас к определению степени с дробным показателем. Остается лишь расписать, при каких m, n и a имеет смысл выражение 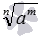. В зависимости от ограничений, накладываемых на m, n и a существуют два основных подхода.
1. Проще всего наложить ограничение на a, приняв a≥0 для положительных m и a>0 для отрицательных m (так как при m≤0 степень 0m не определена). Тогда мы получаем следующее определение степени с дробным показателем.
|
|
Определение.
Степенью положительного числа a с дробным показателем m/n, где m – целое, а n – натуральное число, называется корень n -ой из числа a в степени m, то есть, .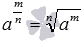
Также определяется дробная степень нуля с той лишь оговоркой, что показатель должен быть положительным.
Определение.
Степень нуля с дробным положительным показателем m/n, где m – целое положительное, а n – натуральное число, определяется как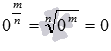 
.
При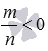 
степень 
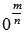не определяется, то есть, степень числа нуль с дробным отрицательным показателем не имеет смысла.
Следует отметить, что при таком определении степени с дробным показателем существует один нюанс: при некоторых отрицательных a и некоторых m и n выражение 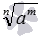имеет смысл, а мы отбросили эти случаи, введя условие a≥0. Например, имеют смысл записи 
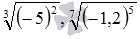или 
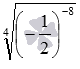, а данное выше определение заставляет нас говорить, что степени с дробным показателем вида 
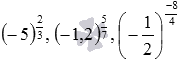не имеют смысла, так как основание не должно быть отрицательным.
2. Другой подход к определению степени с дробным показателем m/n заключается в раздельном рассмотрении четных и нечетных показателях корня 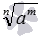. Этот подход требует дополнительного условия: степень числа a, показателем которой является сократимая обыкновенная дробь, считается степенью числа a, показателем которой является соответствующая несократимая дробь (важность этого условия поясним чуть ниже). То есть, если m/n – несократимая дробь, то для любого натурального числа k степень 
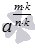предварительно заменяется на 
.
|
|
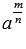При четных n и положительных m выражение 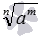имеет смысл при любом неотрицательном a (корень четной степени из отрицательного числа не имеет смысла), при отрицательных m число a должно быть еще отличным от нуля (иначе будет деление на нуль). А при нечетных n и положительных m число a может быть любым (корень нечетной степени определен для любого действительного числа), а при отрицательных m число a должно быть отличным от нуля (чтобы не было деления на нуль).
Приведенные рассуждения приводят нас к такому определению степени с дробным показателем.
Определение.
Пусть m/n – несократимая дробь, m – целое, а n – натуральное число. Для любой сократимой обыкновенной дроби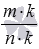 
степень 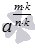заменяется на 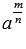. Степень числа a с несократимым дробным показателем m/n - это 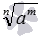для
o любого действительного числа a, целого положительного m и нечетного натурального n, например,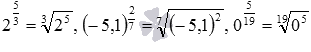 
;
o любого отличного от нуля действительного числа a, целого отрицательного m и нечетного n, к примеру,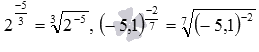 
;
o любого неотрицательного числа a, целого положительного m и четного n, например,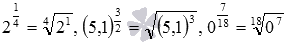 
;
o любого положительного a, целого отрицательного m и четного n, к примеру,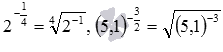 
;
o в остальных случаях степень с дробным показателем не определяется, как например не определены степени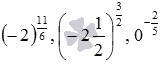 
.
Поясним, зачем степень с сократимым дробным показателем предварительно заменяется степенью с несократимым показателем. Если бы мы просто определили степень 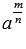как 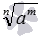, и не оговорились о несократимости дроби m/n, то мы бы столкнулись с ситуациями, подобными следующей: так как 6/10=3/5, то должно выполняться равенство 
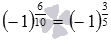, но 
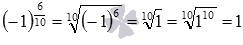, а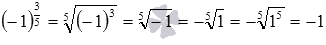 
.
|
|
Заметим, что первое определение степени с дробным показателем удобнее в применении, чем второе. Поэтому мы в дальнейшем будем использовать именно его.
Итак,
Определение.
степень положительного числа a с дробным показателем m/n мы определяем как 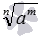, для отрицательных a записи 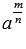мы не придаем никакого смысла, степень числа нуль мы определяем для положительных дробных показателей m/n как 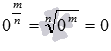, для отрицательных дробных показателей степень числа нуль не определяем.
В заключение этого пункта обратим внимание на то, что дробный показатель степени может быть записан в виде десятичной дроби или смешанного числа, например,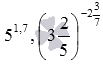 
. Для вычисления значений выражений подобного вида нужно показатель степени записать в виде обыкновенной дроби, после чего воспользоваться определением степени с дробным показателем. Для указанных примеров имеем 
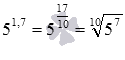и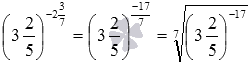 
.