Лекция № 5
Погрешности измерений. Систематические погрешности.
Систематические погрешности. Причины возникновения, оценка.
Систематические погрешности — такие погрешности, которые соответствуют отклонению измеряемой величины от ее истинного значения всегда в одну сторону - либо в сторону завышения, либо в сторону занижения.
Систематические погрешности могут возникать по следующим причинам:
- несоответствие прибора эталону (например, пластмассовые линейки с течением времени обычно укорачиваются на несколько миллиметров);
- неправильное использование прибора (например, перед взвешиванием не установлено равновесие ненагруженных весов).
Систематические погрешности бывают:
а) Конструкционные - обусловлены технологией производства на заводе-изготовителе и связаны с допустимыми разбросами в размерах деталей и значениях электрических компонентов, используемых в данном приборе.
б) Погрешности аппроксимации возникают из-за сделанных предположений относительно зависимостей между величинами. Например, линейная зависимость между двумя величинами часто только предполагается, а на практике это предположение может оказаться только аппроксимацией к истинной зависимости.
в) Погрешности старения вызываются процессами старения приборов, так как детали изнашиваются и их характеристики изменяются, например, из-за слоев грязи, окислов, скопившихся на поверхности деталей.
г) Погрешности подключения возникают, если включение приборов в измерительную цепь приводит к изменению значения самой измеряемой величины. Например, включение амперметра в электрическую цепь для измерения тока в ней приводит к изменению тока в этой цепи из-за сопротивления самого амперметра.
|
|
д) Субъективные систематические погрешности являются следствием индивидуальных свойств человека (заболел, закапаны глаза).
Оценка систематической погрешности проводится в следующей последовательности:
1) в каждой из выбранных точек шкалы прибора определяется среднее арифметическое значение x;
2) систематическая погрешность средства измерений ΔС определяется в каждой из выбранных точек шкалы как разность между средним арифметическим и истинным значением измеряемой величины в этой точке:
ΔС = x –x 0,
где х0 – истинное значение определяемой величины.
Систематическая погрешность ΔС может быть как положительной (при x > x 0), так и отрицательной (при x < x 0).
Истинное значение измеряемой величины x 0, как правило, неизвестно, и вместо x 0 используется действительное значение измеряемой величины, за которое принимают показания образцовых средств измерений.
Систематическая погрешность, подсчитанная по представленной формуле, является абсолютной и имеет ту же размерность, что и измеряемая величина.
Кроме абсолютных значений, подсчитываются относительная δС и приведенная γС систематические погрешности:
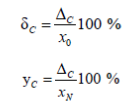
где x N – нормирующее значение (в большинстве случаев х N = х K);
x K – верхний предел шкалы прибора.
Относительная и приведенная погрешности выражаются обычно в процентах, но могут выражаться и в относительных величинах.
Классификация систематических погрешностей. Способы обнаружения и устранения
1. Постоянные систематические погрешности – погрешности, которые в течение всего времени измерений сохраняют свой знак и свое значение (погрешности большинства мер, например, гирь, концевых мер длины, катушек и магазинов сопротивления).
|
|
2. Переменные погрешности при повторных измерениях могут принимать различные значения и в зависимости от характера изменения эти погрешности подразделяют на:
- прогрессивные погрешности – погрешности, которые в процессе измерений возрастают или убывают. Пример: погрешности, возникающие вследствие износа контактирующих деталей средств измерения, постепенное падение напряжения источника тока, питающего измерительную цепь;
- периодические погрешности – погрешности, значения которых являются периодической функцией времени или функцией перемещения указателя измерительного прибора. Пример: средства измерений с круговой шкалой, стрелка которых при измерении совершает несколько оборотов (секундомеры, индикаторы часового типа).
Специальные статистические способы обнаружения систематических погрешностей:
1. Способ последовательных разностей (критерий Аббе) применяется для обнаружения изменяющейся во времени систематической погрешности и состоит в следующем.
Отношение
является критерием для обнаружения систематических погрешностей, где
Это две оценки дисперсии (среднего квадратического отклонения) результатов наблюдений: обычным способом и вычислением суммы квадратов последовательных (в порядке проведения измерений) разностей (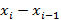
). Отсюда и название метода.
Критическая область для критерия Аббе определяется как:
|
|
где q= 1- P – уровень значимости;
Р – доверительная вероятность.
Значения 
для различных уровней значимости q и числа наблюдений n приведены в таблице.
Таблица 1 – Значения критерия Аббе 
Если полученное значение критерия Аббе меньше 
, то обнаруживается систематическая погрешность результатов измерений.
Пример: На цементном заводе в процессе производства ежедневно в течение 45 дней брались пробы и определялось среднее сопротивление сжатию контрольных кубов (н/см2 или кг/см2). Результаты наблюдения: 40, 33, 75, 18, 62, 33, 38, 69, 65, 100, 124, 91, 79, 42, 63, 23, 47, 52, 98, 97, 73, 85, 88, 40, 42, 51, 23, 75, 52, 126, 90, 111, 92, 109, 72, 28, 56, 17, 52, 68, 75, 102, 107, 77, 45 (всего 45 измерений).
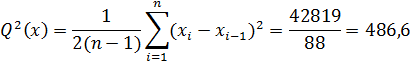
Зададимся уровнем значимости q =0,05. Из таблицы 1 находим 
(45) = 0,7603.
Как видно, полученное значение критерия Аббе меньше 
, следовательно, присутствует систематическая погрешность результатов измерений.
2. Дисперсионный анализ (критерий Фишера) позволяет выяснить наличие систематической погрешности результатов наблюдений, обусловленной влиянием какого-либо постоянно действующего фактора, или определить, вызывают ли изменения этого фактора систематическую погрешность.
В данном случае проводят многократные измерения, состоящие из достаточного числа серий, каждая из которых соответствует различным значениям влияющего фактора. Влияющими факторами, по которым производится объединение результатов наблюдений по сериям, могут быть внешние условия (температура, давление), временная последовательность проведения измерений и т.п.
После проведения N измерений их разбивают на s серий (s> 3) по nj результатов наблюдений в каждой серии и затем устанавливают, имеетсяили отсутствует систематическое расхождение между результатаминаблюдений в различных сериях.
Критерием оценки наличия систематических погрешностей в данном случае является дисперсионный критерий Фишера:
где 
– межсерийная дисперсия, выражает силу действия фактора, вызывающего систематические различия между сериями;
– внутрисерийная дисперсия, характеризует случайные погрешности измерений, обуславливающие различия (отклонения результатов наблюдений) внутри серии.
Критическая область для критерия Фишера соответствует P(F > Fq) = q.
Значения Fq для различных уровней значимости q, числа измерений N и числа серий s приведены в таблице 2.
Таблица 2 - Значения критерия Фишера
| Fq при к1, равном | |||||||
| 98,49 | 99,00 | 99,17 | 99,25 | 99,30 | 99,33 | 99,36 | 99,42 | |
| 21,20 | 18,00 | 16,69 | 15,98 | 15,52 | 15,21 | 14,80 | 14,37 | |
| 13,74 | 10,92 | 9,78 | 9,15 | 8,75 | 8,47 | 8,10 | 7,72 | |
| 11,26 | 8,65 | 7,59 | 7,01 | 6,63 | 6,37 | 6,03 | 5,67 | |
| 10,04 | 7,56 | 6,55 | 5,99 | 5,64 | 5,39 | 5,06 | 4,71 | |
| 9,33 | 6,93 | 5,95 | 5,41 | 5,06 | 4,82 | 4,50 | 4,16 | |
| 8,86 | 6,51 | 5,56 | 5,03 | 4,69 | 4,46 | 4,14 | 3,80 | |
| 8,53 | 6,23 | 5,29 | 4,77 | 4,44 | 4,20 | 3,89 | 3,55 | |
| 8,28 | 6,01 | 5,09 | 4,58 | 4,25 | 4,01 | 3,71 | 3,37 | |
| 8,10 | 5,85 | 4,94 | 4,43 | 4,10 | 3,87 | 3,56 | 3,23 | |
| 7,56 | 5,39 | 4,51 | 4,02 | 3,70 | 3,47 | 3,17 | 2,84 |
Для определения Fq необходимо вычислить 
= N-s и 
= s-1. Причем, – это число степеней свободы большей дисперсии, к1– число степеней свободы меньшей дисперсии.
Если полученное значение критерия Фишера больше Fq, то гипотеза об отсутствии систематических смещений результатов наблюдений по сериям отвергается, т.е. обнаруживается систематическая погрешность, вызываемая тем фактором, по которому группировались результаты наблюдений.
Дисперсионный анализ (критерий Фишера) является наиболее эффективным и достоверным, так как позволяет не только установить факт наличия погрешности, но и дает возможность проанализировать источники ее возникновения.
Дисперсионный анализ (критерий Фишера). В практике измерений часто бывает необходимо выяснить наличие систематической погрешности результатов наблюдений, обусловленной влиянием какого-либо постоянно действующего фактора, или определить, вызывают ли изменения этого фактора систематическое смещение результатов измерений. В данном случае проводят многократные измерения, состоящие из достаточного числа серий, каждая из которых соответствует определенным (пусть неизвестным, но различным) значениям влияющего фактора. Влияющими факторами, по которым производится объединение результатов наблюдений по сериям, могут быть внешние условия (температура, давление и т.д.), временная последовательность проведения измерений и т.п. 
После проведения N измерений их разбивают на s серий (s > 3) по nj результатов наблюдений (snj= N) в каждой серии и затем устанавливают, имеется или отсутствует систематическое расхождение между результатами наблюдений в различных сериях. При этом должно быть установлено, что результаты в сериях распределены нормально. Рассеяние результатов наблюдений в пределах каждой серии отражает только случайные влияния, характеризует лишь случайные погрешности измерений в пределах этой серии. Характеристикой совокупности случайных внутрисерийных погрешностей будет средняя сумма дисперсий результатов наблюдений, вычисленных раздельно для каждой серии, т.е.
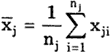
где xji - результат i-го измерения в j-й серии.
Внутрисерийная дисперсия 
2BC характеризует случайные погрешности измерений, так как только случайные влияния обусловливают те различия (отклонения результатов наблюдений), на которых она основана. В то же время рассеяние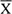 
j различных серий обусловливается не только случайными погрешностями измерений, но и систематическими различиями (если они существуют) между результатами наблюдений, сгруппированными по сериям. Следовательно, усредненная межсерийная дисперсия
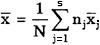
где 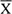, выражает силу действия фактора, вызывающего систематические различия между сериями.
Таким образом, 2BC /( 2BC+ 2MC) характеризует долю дисперсии всех результатов наблюдений, обусловленную наличием случайных погрешностей измерений, а 2MC /( 2BC+ 2MC) - долю дисперсии, обусловленную межсерийными различиями результатов наблюдений. Первую из них называют коэффициентом ошибки, вторую - показателем дифференциации. Чем больше отношение показателя дифференциации к коэффициенту ошибки, тем сильнее действие фактора, по которому группировались серии, и тем больше систематическое различие между ними.
Критерием оценки наличия систематических погрешностей в данном случае является дисперсионный критерий Фишера F= 2MC 2BC. Критическая область для критерия Фишера соответствует P(F>Fq)=q.
Значения Fq для различных уровней значимости q, числа измерений N и числа серий s приведены в приложении 1, где k2=N-s, k1=s-1. Если полученное значение критерия Фишера больше Fq (при заданных q, N и s), то гипотеза об отсутствии систематических смещений результатов наблюдений по сериям отвергается, т.е. обнаруживается систематическая погрешность, вызываемая тем фактором, по которому группировались результаты наблюдений.
Из всех рассмотренных способов обнаружения систематических погрешностей дисперсионный анализ является наиболее эффективным и достоверным, так как позволяет не только установить факт наличия погрешности, но и дает возможность проанализировать источники ее возникновения.